Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-15T19:14:10.588Z Has data issue: false hasContentIssue false
  • English
  • Français

A test for commutators

Published online by Cambridge University Press:  18 May 2009

Hans Liebeck
Hans Liebeck
Affiliation:
The University, Keele, Staffs. ST5 5BG
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In the course of a study of commutator subgroups I. D. Macdonald [1] presented the free nilpotent group G4 of class 2 on 4 generators as an example of a nilpotent group whose commutator subgroup has elements that are not commutators. To demonstrate this he proceeded as follows: let G4 = 〈a1, a2, a3, a4〉 and put cij = [ai, aj] for 1 ≦ i < j ≦ 4. Then the relations in G4 are [cij, ak] = 1 for 1 ≦ i < j ≦ 4 and 1 ≦ k ≦ 4, and their consequences. Macdonald observed that an arbitrary commutator may be written as

which simplifies to

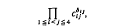
where δij = αiβj - αjβi The indices δij satisfy the relation

It follows that the element c13c24 in G′4 (for which δ12 = δ14 = δ23 = δ34 = 0 and δ13 = δ24 = 1) is not a commutator.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 17 , Issue 1 , January 1976 , pp. 31 - 36
Copyright
Copyright © Glasgow Mathematical Journal Trust 1976

References

REFERENCES

1.Macdonald, I. D., On a set of normal subgroups, Proc. Glasgow Math. Soc. 5 (1962), 137–146.Google Scholar
2.Macdonald, I. D., On cyclic commutator subgroups, J. London Math. Soc. 38 (1963), 419–422.CrossRefGoogle Scholar
3.Rodney, D. M., Commutators and conjugacy in groups, Ph.D. thesis, University of Keele (1974).Google Scholar