No CrossRef data available.
Article contents
Toeplitz and Hankel operators on Bargmann spaces
Published online by Cambridge University Press: 18 May 2009
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Let μ be the Gaussian measure in ℂn given by dμ(z)=(2π)−n exp(−|z|2/2)dV, where dV is the ordinary Lebesgue measure in ℂn. The Segal-Bargmann space H2(μ) is the space of all entire functions on ℂn that belong to L2(μ)-the usual space of Gaussian square-integrable functions. Let P be the orthogonal projection from L2(μ) onto H2(μ). For a measurable function ϕ on ℂn, the multiplication operator Mϕ on L2(μ) is defined by Mϕh =ϕh. The Toeplitz operator Tϕ is defined on H2(μ)by
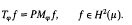
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Glasgow Mathematical Journal Trust 1988
References
1.Berezin, F. A., Covariant and contravariant symbols of operators, Jzw. AN SSSR, 35 (1972), 1134–1167 (Russian).Google Scholar
2.Berger, C. A. and Coburn, L. A., Toeplitz operators and quantum mechanics, J. Functional Analysis 68 (1986), 273–299.CrossRefGoogle Scholar
3.Berger, C. A. and Coburn, L. A., Toeplitz operators on the Segal–Bargmann space, Trans. Amer. Math. Soc. 301 (1987), 813–829.CrossRefGoogle Scholar
4.Gohberg, J. C. and Krein, M. G., Introduction to the theory of non-selfadjoint operators in Hilbert space, (Nauka 1965), (Russian).Google Scholar
5.Halmos, P. R. and Sunder, V. S., Bounded integral operators on L2 spaces, (Springer-Verlag, 1978).CrossRefGoogle Scholar
6.Howe, R., Quantum mechanics and partial differential equations J. Functional Analysis 38 (1980) 188–254.CrossRefGoogle Scholar
7.Janson, S.,Peetre, J. and Rochberg, R., Hankel forms and the Fock space (preprint-1986).CrossRefGoogle Scholar
8.Pokrzywa, A., On continuity of spectra in norms ideals, Linear Algebra and Appl. 69 (1985) 121–130.CrossRefGoogle Scholar
9.Russo, B., On the Hausdorff–Young theorem for integral operators, Pacific. J. Math. 68 (1977), 241–253.CrossRefGoogle Scholar

