No CrossRef data available.
Article contents
Toeplitz operators and algebras of bounded analytic functions on the disk
Published online by Cambridge University Press: 18 May 2009
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Here and throughout, A is a closed subalgebra of H∞ that contains the disk algebra and M(A) denotes the maximal ideal space of A. Because A contains the function fo(z) = z, we can define the fiber Mλ(A) of M(A) for λ ε ∂D (the unit circle) in the usual way; i.e., Mλ(A) = {φ ∈ M(A): fo(φ) = λ}. The Bergman space  of the unit disk D is the L2(D, dx dy)-closure of A. Let
of the unit disk D is the L2(D, dx dy)-closure of A. Let 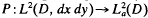 be the orthogonal projection. For f ∈ L∞(D, dx dy), define the multiplication operator Mf: L2(D, dx dy)→ L2, (D, dx dy) by
be the orthogonal projection. For f ∈ L∞(D, dx dy), define the multiplication operator Mf: L2(D, dx dy)→ L2, (D, dx dy) by
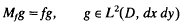
and define the Toeplitz operator 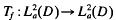 by
by
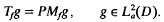
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Glasgow Mathematical Journal Trust 1991
References
REFERENCES
1.Chang, S. Y. and Marshall, D., Some algebras of bounded analytic functions containing the disk algebra, in Banach spaces of analytic functions, Lecture Notes in Math. 604, Springer Verlag, 1977.Google Scholar
2.Coburn, L., Singular integral operators and Toeplitz operators on odd spheres, Indiana Univ. Math. J. 23, (1973), 433–439.CrossRefGoogle Scholar
7.Luecking, D., Inequalities on Bergman spaces, Illinois J. Math. 25 (1981), 1–11.CrossRefGoogle Scholar
8.McDonald, G. and Sundberg, C., Toeplitz operators on the disk, Indiana Univ. Math. J. 28 (1979), 595–611.CrossRefGoogle Scholar
10.Smith, R., Toeplitz operators on abstract Hardy spaces, Glasgow Math. J. 30 (1988), 129–131.CrossRefGoogle Scholar
11.Sundberg, C., Exact sequences for generalized Toeplitz operators, Proc. Amer. Math. Soc. 101 (1987), 634–636.CrossRefGoogle Scholar

