Article contents
Toeplitz operators on abstract Hardy spaces
Published online by Cambridge University Press: 18 May 2009
Extract
In [10], C. Sundberg uses a clever argument involving an idea of Davie and Jewell [13] to prove an isomorphism theorem for a very general class of operators. A related spectral inclusion theorem is an immediate consequence of the proof of this result, as Sundberg points out. He goes on to list several well known examples that are applications of his main result and remarks that the proof of the McDonald–Sundberg theorem (c.f. [9]) can now be considerably simplified. The purpose of this note is to give further evidence of the utility of the criterion established in [10]. Here and throughout X denotes a compact Hausdorff space and A is a function algebra on X. The Shilovboundary of A is the minimal closed subset ∂(A) of X with the property that
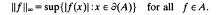 .
.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Glasgow Mathematical Journal Trust 1988
References
- 1
- Cited by

