Topological invariants of germs of real analytic functions

Extract

Let f: (ℝⁿ, 0)→ (ℝ,0) be a germ of a real analytic function. Let L and F(f) denote the link of f and the Milnor fibre of f_c respectively, i. e., L = {x ∈ Sⁿ⁻¹ | f(x) = 0}, 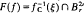, where 0 ≤ ξ ≪ r ≪ 1, 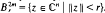. In [2] Szafraniec introduced the notion of an 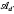-germ as a generalization of a germ defined by a weighted homogeneous polynomial satisfying some condition concerning the relation between its degree and weights (definition 1). He also proved that if f is an 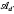-germ (presumably with nonisolated singularity) then the number χ(F(f)/d mod 2 is a topological invariant of f, where χ(F(f)) is the Euler characterististic of F(f), and gave the formula for χ(L)/2 mod 2 (it is a well-known fact that F(L) is an even number). As a simple consequence he got the fact that χ(F(f)mod 2 is a topological invariant for any f, which is a generalization of Wall's result [3] (he considered only germs with an isolated singularity).