No CrossRef data available.
Article contents
Topologies on Boolean algebras defined by ideals and dual ideals
Published online by Cambridge University Press: 18 May 2009
Extract
In the paper [5], Rema used the well-known fact that in a Boolean algebra 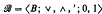 the binary operation d: B × B → B defined by
the binary operation d: B × B → B defined by 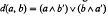 is a “metric“ operation to show that, if D is any dual ideal of ^, then the sets Up = {(x, y): d(x, y) <p}, where p ∈ D, form a base for a uniformity of }, the resulting topological space <B; T[D]> being called an auto-topologized Boolean algebra. Recently, Kent and Atherton [1, 4] exhibited a family of topologies on an arbitrary lattice ℒ defined in terms of ideals and dual ideals. More specifically, if I and D are respectively an ideal and a dual ideal of ℒ, then the T[I:D] topology on ℒ is the topology defined by taking the sets of the form a*⋂b+, where
is a “metric“ operation to show that, if D is any dual ideal of ^, then the sets Up = {(x, y): d(x, y) <p}, where p ∈ D, form a base for a uniformity of }, the resulting topological space <B; T[D]> being called an auto-topologized Boolean algebra. Recently, Kent and Atherton [1, 4] exhibited a family of topologies on an arbitrary lattice ℒ defined in terms of ideals and dual ideals. More specifically, if I and D are respectively an ideal and a dual ideal of ℒ, then the T[I:D] topology on ℒ is the topology defined by taking the sets of the form a*⋂b+, where 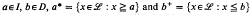 , as sub-base for the open sets. It is these topologies that are studied in this paper.
, as sub-base for the open sets. It is these topologies that are studied in this paper.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Glasgow Mathematical Journal Trust 1973

