Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-15T15:25:39.132Z Has data issue: false hasContentIssue false
  • English
  • Français

Transversally affine foliations

Published online by Cambridge University Press:  18 May 2009

P. M. D. Furness  and
E. Fédida
P. M. D. Furness
Affiliation:
Department of Mathematics, University of Southampton, Southampton, SO9 5NH
E. Fédida
Affiliation:
Institut de Recherche Mathematique Avancee, Université Louis Pasteur, 7, Rue Rene Descartes, 67084 Strasbourg Cedex
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let ℱ be a smooth foliation of codimension p on a smooth manifold Mm. We can define ℱ by an atlas of coordinate charts (U, (x, y)), called leaf charts, where (x, y): U → Rm−p × Rp are coordinate functions for which the leaves of ℱ are given by y1 constant,…,yp constant, in U. Clearly, on the overlap of two such leaf charts (U, (x, y)) and (U′, (x′, y′)) we have a coordinate transformation of the form

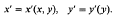
If y′ is always affine in y, i.e.

where 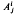and Bi are constants, we shall say that ℱ is a transversally affine foliation. This notion is, in a sense, dual to that of affine foliation, see [2], in which x′ is affine in x and each leaf has an induced flat affine structure.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 17 , Issue 2 , July 1976 , pp. 106 - 111
Copyright
Copyright © Glasgow Mathematical Journal Trust 1976

References

REFERENCES

1.Fédida, E., Feuilletages du plan—feuilletages de Lie, Thesis, University of Strasbourg (1973).Google Scholar
2.Furness, P. M. D., Affine foliations of codimension one, Quart. J. Math. Oxford (2) 25 (1974), 151–161.CrossRefGoogle Scholar
3.Furness, P. M. D. and Arrowsmith, D. K., Locally symmetric spaces, J. London Math. Soc. (2) 10 (1975), 487–499.CrossRefGoogle Scholar
4.Furness, P. M. D. and Robertson, S. A., Parallel framings and foliations on pseudo-riemannian manifolds, J. Differential Geometry 9 (1974), 409–422.Google Scholar
5.Godbillon, C. and Vey, J., Un invariant des feuilletages de codimension 1, C. R. Acad. Sci. Paris Sér. A 273, (1971), 92–95.Google Scholar
6.Haefliger, A., Variétes feuilletées, Ann. Scuola Norm. Sup. Pisa. 16 (1962), 367–397.Google Scholar
7.Hector, G., Groupes de diffeomorphisms et feuilletages analytiques; to appear.Google Scholar
8.Kobayashi, S. and Nomizu, K., Foundations of differential geometry (Interscience, 1963).Google Scholar
9.Moussu, R., Feuilletages sans holonomie d'une variété fermée, C. R. Acad. Set. Paris Sér. A 270 (1970), 1308–1311.Google Scholar
10.Reeb, G., Sur certaines propriétés topologiques des variétes feuilletées, Actualités Sci. Indust. (Hermann, 1952).Google Scholar
11.Tischler, D., On fibering certain foliated manifolds over S 1, Topology 9 (1970), 153–154.CrossRefGoogle Scholar
12.Walker, A. G., Canonical form for a riemannian space with a parallel field of null planes, Quart. J. Math. Oxford (2) 1 (1950), 69–79.CrossRefGoogle Scholar