Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-15T11:27:37.128Z Has data issue: false hasContentIssue false
  • English
  • Français

Union results for thin sets

Published online by Cambridge University Press:  18 May 2009

Kathryn E. Hare
Kathryn E. Hare
Affiliation:
Department of Pure MathematicsUniversity of WaterlooWaterloo, Ontari O N2L 3G1 Canada
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let G be a compact abelian group and let Γ be its (discrete) dual group. Denote by M(G) the space of complex regular Borel measures on G.

Let E be a subset of Γ. Then:

(i) E is called a Rajchman set if, for all μ ∈M(G) 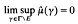implies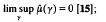

(ii) E is called a set of continuity if given ε > 0 there exists δ > 0 such that if 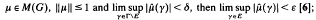and

(iii) E is called a parallelepiped of dimension N if |E| = 2N and there are two-element sets 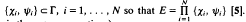. (The multiplication indicated here is the group operation.)

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 32 , Issue 2 , May 1990 , pp. 241 - 254
Copyright
Copyright © Glasgow Mathematical Journal Trust 1990

References

REFERENCES

1.Blei, R., Fractional Cartesian products of sets, Ann. last. Fourier (Grenoble) 29 (1979), 79–105.CrossRefGoogle Scholar
2.De Leeuw, K. and Katznelson, Y., The two sides of a Fourier-Stieltjes transform and almost idempotent measures, Israel J. Math. 8 (1970), 213–229.CrossRefGoogle Scholar
3.Edwards, R. E. and Ross, K. A., p-Sidon sets, J. Fund. Anal. 15 (1974), 404–427.CrossRefGoogle Scholar
4.Erdös, P. and Rényi, A., Additive properties of random sequences of positive integers, Ada Arith. 6 (1960), 83–110.CrossRefGoogle Scholar
5.Fournier, J. and Pigno, L., Analytic and arithmetic properties of thin sets, Pacific J. Math. 105 (1983), 115–141.CrossRefGoogle Scholar
6.Gardner, P. and Pigno, L., The two sides of a Fourier-Stieltjes transform, Arch. Math. (Basel) 32 (1979), 75–78.CrossRefGoogle Scholar
7.Hajela, D., Construction techniques for some thin sets in duals of compact abelian groups, Ann. Inst. Fourier (Grenoble) 36 (1986), 137–166.CrossRefGoogle Scholar
8.Halberstam, H. and Roth, K., Sequences, Volume 1 (Clarendon Press, 1966).Google Scholar
9.Hare, K. E., Arithmetic properties of thin sets, Pacific J. Math. 131 (1988), 143–155.CrossRefGoogle Scholar
10.Host, B. and Parreau, F., Ensembles de Rajchman et ensembles de continuity, C.R. Acad. Sci. Paris Sir. I Math. 288 (1979), 899–902.Google Scholar
11.Host, B. and Parreau, F., Sur les mesures dont la transformed de Fourier Stieltjes ne tend pas vers zero a l'infini, Colloq. Math. 41 (1979), 285–289.CrossRefGoogle Scholar
12.Johnson, G. W. and Woodward, G. S., Onp-Sidon sets, Indiana Univ. Math. J. 24 (1974), 161–167.CrossRefGoogle Scholar
13.Lopez, J. and Ross, K., Sidon sets, Lecture notes in Pure and Applied Mathematics 13 (Marcel Dekker, 1975).Google Scholar
14.Miheev, I., Trigonometric series with gaps, Anal. Math. 9 (1983), 43–55.CrossRefGoogle Scholar
15.Pigno, L., Fourier transforms which vanish at infinity off certain sets, Glasgow Math. J. 19 (1978), 49–56.CrossRefGoogle Scholar
16.Rajchman, A., Une classe de series trigonom6triques qui convergent presque partout vers zéro, Math. Ann. 101 (1929), 686–700.CrossRefGoogle Scholar
17.Rudin, W., Trigonometric series with gaps, J. Math. Mech. 9 (1960), 203–227.Google Scholar