Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-15T13:56:10.103Z Has data issue: false hasContentIssue false
  • English
  • Français

Unique factorization in Cayley arithmetics and cryptology

Published online by Cambridge University Press:  18 May 2009

P. J. C. Lamont
P. J. C. Lamont
Affiliation:
Department of Computer Science, College of Applied Sciences, Western Illinois University, Macomb, Illinois 61455, U.S.A.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 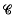be the classical Cayley algebra defined over the reals with basis 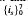where 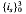gives a quaternion algebra ℋ4 with i0 = 1, i1i2i3 = −1, i1i4 = i5, i2i4 = i6 and i3i4 = i7. The multiplication table of the imaginary basic units follows:

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 33 , Issue 3 , September 1991 , pp. 267 - 273
Copyright
Copyright © Glasgow Mathematical Journal Trust 1991

References

REFERENCES

1.van der Blij, F., History of the octaves, Simon Stevin 34 (1961), 106–125.Google Scholar
2.van der Blij, F. and Springer, T. A., The arithmetics of the octaves and of the group G2, Nederl. Akad. Wetensch. Proc. (=Indag. Math.) 62A (1959), 406–418.CrossRefGoogle Scholar
3.Dickson, L. E., On quaternions and their generalization and the history of the eight square theorem, Annals of Math. (2), 20 (1919), 155–171, 297.CrossRefGoogle Scholar
4.Hurwitz, A., Über die Composition der quadratischen Formen von beliebig vielen Variabeln, Nachr. Gesell. Wiss. Göttingen (1898), 309–316.Google Scholar
5.Lamont, P. J. C., Arithmetics in Cayley's algebra, Proc. Glasgow Math. Assoc. 6 (1963), 99–106.CrossRefGoogle Scholar
6.Lamont, P. J. C., Ideals in Cayley's algebra, Nederl. Akad. Wetensch. Proc. (= Indag. Math.) 66A (1963), 394–400.CrossRefGoogle Scholar
7.Lamont, P. J. C., Approximation theorems for the group G2, Nederl. Akad. Wetensch. Proc. (=Indag. Math.) 67A (1964), 187–192.CrossRefGoogle Scholar
8.Lamont, P. J. C., Factorization and arithmetic functions for orders in composition algebras, Glasgow Math. J. 14 (1973), 86–95.CrossRefGoogle Scholar
9.Lamont, P. J. C., The number of Cayley integers of given norm, Proc. Edinburgh Math. Soc. 25 (1982), 101–103.CrossRefGoogle Scholar
10.Lamont, P. J. C., Computer generated natural inner automorphisms of Cayley's algebra, Glasgow Math. J. 23 (1982), 187–189.CrossRefGoogle Scholar
11.Lamont, P. J. C., The nonexistence of a factorization formula for Cayley numbers, Glasgow Math. J. 24 (1983), 131–132.CrossRefGoogle Scholar
12.Rankin, R. A., On representations of a number as a sum of squares and certain related identities, Proc. Camb. Phil. Soc. 41 (1945), 1–11.CrossRefGoogle Scholar
13.Rankin, R. A., A certain class of multiplicative functions, Duke Math. J. 13 (1946), 281–306.CrossRefGoogle Scholar
14.Taussky, O., Sums of squares, Amer. Math. Monthly 77 (1970), 805–830.CrossRefGoogle Scholar
15.Welsh, D., Codes and Cryptography (Oxford, 1988).Google Scholar