No CrossRef data available.
Published online by Cambridge University Press: 25 February 2013
We prove uniqueness of positive solutions for the boundary value problems
where Ω is a bounded domain in ℝn with smooth boundary ∂Ω, λ is a positive parameter and f:(0,∞) → (0,∞) is sublinear at ∞ and is allowed to be singular at 0.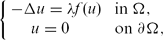 \[
\{\begin{array}{ll} -\Delta u=\lambda f(u)\ \ &\text{in}\Omega, \ \ \ \ \ u=0 &\text{on \partial \Omega,
\]
\[
\{\begin{array}{ll} -\Delta u=\lambda f(u)\ \ &\text{in}\Omega, \ \ \ \ \ u=0 &\text{on \partial \Omega,
\]