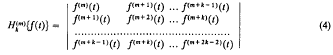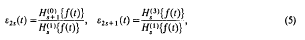Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Wynn, P.
1968.
Upon the definition of an integral as the limit of a continued fraction.
Archive for Rational Mechanics and Analysis,
Vol. 28,
Issue. 2,
p.
83.
Gray, H. L.
Atchison, T. A.
and
McWilliams, G. V.
1971.
Higher OrderG-Transformation.
SIAM Journal on Numerical Analysis,
Vol. 8,
Issue. 2,
p.
365.
Gragg, W. B.
1972.
The Padé Table and Its Relation to Certain Algorithms of Numerical Analysis.
SIAM Review,
Vol. 14,
Issue. 1,
p.
1.
Pye, W. C.
and
Atchison, T. A.
1973.
An Algorithm for the Computation of the Higher OrderG-Transformation.
SIAM Journal on Numerical Analysis,
Vol. 10,
Issue. 1,
p.
1.
Wynn, P.
1973.
Upon some continuous prediction algorithms. II.
Calcolo,
Vol. 9,
Issue. 4,
p.
235.
Levin, David
1980.
On accelerating the convergence of infinite double series and integrals.
Mathematics of Computation,
Vol. 35,
Issue. 152,
p.
1331.
Levin, David
and
Sidi, Avram
1981.
Two New Classes of Nonlinear Transformations for Accelerating the Convergence of Infinite Integrals and Series.
Applied Mathematics and Computation,
Vol. 9,
Issue. 3,
p.
175.
Marziani, M. F.
1983.
A connection between borel and padé summation techniques.
Lettere Al Nuovo Cimento Series 2,
Vol. 37,
Issue. 3,
p.
124.
Nagai, Atsushi
Tokihiro, Tetsuji
and
Satsuma, Junkichi
1998.
The Toda molecule equation and the 𝜖-algorithm.
Mathematics of Computation,
Vol. 67,
Issue. 224,
p.
1565.
Safouhi, Hassan
2000.
The HD and HD̄ Methods for Accelerating the Convergence of Three-Center Nuclear Attraction and Four-Center Two-Electron Coulomb Integrals over B Functions and Their Convergence Properties.
Journal of Computational Physics,
Vol. 165,
Issue. 2,
p.
473.
Brezinski, Claude
2002.
Computational Aspects of Linear Control.
Vol. 1,
Issue. ,
p.
255.
Safouhi, Hassan
and
Berlu, Lilian
2006.
The Fourier transform method and the SD¯ approach for the analytical and numerical treatment of multicenter overlap-like quantum similarity integrals.
Journal of Computational Physics,
Vol. 216,
Issue. 1,
p.
19.
Safouhi, Hassan
and
Bouferguene, Ahmed
2006.
Extrapolation methods for improving convergence of spherical Bessel integrals for the two‐center Coulomb integrals.
International Journal of Quantum Chemistry,
Vol. 106,
Issue. 11,
p.
2318.
Slevinsky, Mikael
and
Safouhi, Hassan
2008.
Numerical treatment of a twisted tail using extrapolation methods.
Numerical Algorithms,
Vol. 48,
Issue. 4,
p.
301.
Safouhi, Hassan
2010.
Bessel, sine and cosine functions and extrapolation methods for computing molecular multi-center integrals.
Numerical Algorithms,
Vol. 54,
Issue. 1,
p.
141.
Brezinski, Claude
and
Redivo–Zaglia, Michela
2019.
The genesis and early developments of Aitken’s process, Shanks’ transformation, the ε–algorithm, and related fixed point methods.
Numerical Algorithms,
Vol. 80,
Issue. 1,
p.
11.
Brezinski, C.
2019.
Reminiscences of Peter Wynn.
Numerical Algorithms,
Vol. 80,
Issue. 1,
p.
5.
Brezinski, Claude
and
Redivo-Zaglia, Michela
2020.
Extrapolation and Rational Approximation.
p.
85.
Brezinski, Claude
Norman, F. Alexander
and
Redivo-Zaglia, Michela
2021.
The Legacy of Peter Wynn.
Mathematics,
Vol. 9,
Issue. 11,
p.
1240.
Slevinsky, Richard M.
and
Safouhi, Hassan
2022.
Compact formulae for three-center nuclear attraction integrals over exponential type functions.
Journal of Mathematical Chemistry,
Vol. 60,
Issue. 7,
p.
1337.