Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Gupta, Anupam
2001.
Improved Bandwidth Approximation for Trees and Chordal Graphs.
Journal of Algorithms,
Vol. 40,
Issue. 1,
p.
24.
Slinko, Arkadii
2002.
On Asymptotic Strategy-Proofness of Classical Social Choice Rules.
Theory and Decision,
Vol. 52,
Issue. 4,
p.
389.
Slinko, Arkadii
2004.
How large should a coalition be to manipulate an election?.
Mathematical Social Sciences,
Vol. 47,
Issue. 3,
p.
289.
Akhtar, Reza
Jiang, Tao
and
Miller, Zevi
2008.
Asymptotic Determination of Edge-Bandwidth of Multidimensional Grids and Hamming Graphs.
SIAM Journal on Discrete Mathematics,
Vol. 22,
Issue. 2,
p.
425.
Noel, Jonathan A.
Scott, Alex
and
Sudakov, Benny
2018.
Supersaturation in posets and applications involving the container method.
Journal of Combinatorial Theory, Series A,
Vol. 154,
Issue. ,
p.
247.
Girão, António
Illingworth, Freddie
Michel, Lukas
Savery, Michael
and
Scott, Alex
2024.
Flashes and Rainbows in Tournaments.
Combinatorica,
Vol. 44,
Issue. 3,
p.
675.

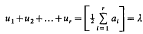
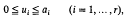
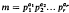 which contain exactly λ prime factors counted according to multiplicity, and is therefore, as is proved in [1], the cardinality of the largest possible set of divisors of
which contain exactly λ prime factors counted according to multiplicity, and is therefore, as is proved in [1], the cardinality of the largest possible set of divisors of 