Hostname: page-component-cb9f654ff-d5ftd Total loading time: 0 Render date: 2025-08-19T17:51:14.837Z Has data issue: false hasContentIssue false
  • English
  • Français

A VARIANT ON THE NOTION OF A DIOPHANTINE s-TUPLE

Published online by Cambridge University Press:  01 January 2009

WILLIAM D. BANKS ,
FLORIAN LUCA  and
LÁSZLÓ SZALAY
WILLIAM D. BANKS*
Affiliation:
Department of MathematicsUniversity of MissouriColumbia, MO 65211USA e-mail: bbanks@math.missouri.edu
FLORIAN LUCA
Affiliation:
Instituto de MatemáticasUniversidad Nacional Autónoma de MéxicoC.P. 58089, Morelia, Michoacán, México e-mail: fluca@matmor.unam.mx
LÁSZLÓ SZALAY
Affiliation:
Institute of Mathematics and StatisticsUniversity of West HungaryH-9400 Sopron, Erzsébet u. 9, Hungary e-mail: laszalay@ktk.nyme.hu
*
†Corresponding author.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We show that there is an infinite set 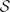of natural numbers with the property that 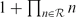is square-free for every finite subset ⊆ .

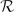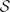Keywords

MSC Numbers: 11B9911N25

Information

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 51 , Issue 1 , January 2009 , pp. 83 - 89
Copyright
Copyright © Glasgow Mathematical Journal Trust 2008

References

REFERENCES

1.Baker, A. and Davenport, H., The equations 3x 2 − 2 = y 2 and 8x 2 − 7 = z 2, Quart. J. Math. Oxford Ser. 20 (2) (1969), 129–137.CrossRefGoogle Scholar
2.Dickson, L. E., A new extension of Dirichlet's theorem on prime numbers, Messenger Math. 33 (1904), 155–161.Google Scholar
3.Dujella, A., There are only finitely many Diophantine quintuples, J. Reine Angew. Math. 566 (2004), 183–214.Google Scholar
4.Luca, F. and Shparlinski, I. E., Approximating positive reals by ratios of kernels of consecutive integers, in Diophantine analysis and related fields, Sem. Math. Sci. 35 (Keio Univ., Yokohama, 2006). 141–148.Google Scholar
5.Tenenbaum, G., Introduction to analytic and probabilistic number theory. Cambridge Studies in Advanced Mathematics, 46 (Cambridge University Press, Cambridge, 1995).Google Scholar
6.Terr, D., Solution of problem H-520, Fibonacci Quart. 36 (1998), 94–95.Google Scholar