Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-15T10:13:56.713Z Has data issue: false hasContentIssue false
  • English
  • Français

A weaker condition for normality

Published online by Cambridge University Press:  18 May 2009

Ian Doust
Ian Doust
Affiliation:
School of Mathematics, University of New South Wales, Kensington, NSW 2033, Australia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

One of the most important results of operator theory is the spectral theorem for normal operators. This states that a normal operator (that is, a Hilbert space operator T such that T*T= TT*), can be represented as an integral with respect to a countably additive spectral measure,

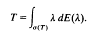
Here E is a measure that associates an orthogonal projection with each Borel subset of ℂ. The countable additivity of this measure means that if x Eℋ can be written as a sum of eigenvectors 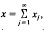then this sum must converge unconditionally.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 36 , Issue 2 , May 1994 , pp. 249 - 253
Copyright
Copyright © Glasgow Mathematical Journal Trust 1994

References

REFERENCES

1.Berkson, E. and Gillespie, T. A., Absolutely continuous functions of two variables and well-bounded operators, J. London Math. Soc. (2) 30 (1984), 305–321.CrossRefGoogle Scholar
2.Doust, I., Well-bounded and scalar-type spectral operators on L4 spaces, J. London Math. Soc. (2) 39 (1989), 525–534.Google Scholar
3.Doust, I., Well-bounded and scalar-type spectral operators on spaces not containing c0, Proc. Amer. Math. Soc. 105 (1989), 367–370.Google Scholar
4.Doust, I., An example in the theory of spectral and well-bounded operators, Miniconference on Operators in Analysis (Sydney, 1989), Proc. Centre Math. Anal. Austral. Nat. Univ. 24 (1990), 83–90.Google Scholar
5.Dowson, H. R., Spectral theory of linear operators, London Mathematical Society Monographs 12 (Academic Press, 1978).Google Scholar
6.Fong, C. K. and Lam, L.. On spectral theory and convexity, Trans. Amer. Math. Soc. 264 (1981), 59–75.CrossRefGoogle Scholar
7.Hardy, G. H., On double Fourier series, Quart. J. Math. 37 (1906), 53–79.Google Scholar
8.Hobson, E. W., The theory of functions of a real variable and the theory of Fourier's series, Vol. 1, third edition (Dover, 1957).Google Scholar
9.McCarthy, C. A., Commuting Boolean algebras of projections II, Proc. Amer. Math. Soc. 15 (1964), 781–787.Google Scholar
10.Ringrose, J. R., On well-bounded operators, J. Austral. Math. Soc. 1 (1959 1960), 334–343.CrossRefGoogle Scholar
11.Smart, D. R., Conditionally convergent spectral expansions, J. Austral. Math. Soc. 1 (1959 1960), 319–333.CrossRefGoogle Scholar