Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Barnes, Bruce A.
1999.
Riesz points and Weyl's theorem.
Integral Equations and Operator Theory,
Vol. 34,
Issue. 2,
p.
187.
Chō, M.
and
Nagano, Y.
1999.
Simple proof of thep-hyponormality of the Aluthge transformation.
Integral Equations and Operator Theory,
Vol. 33,
Issue. 2,
p.
248.
Jeon, In Ho
2001.
Weyl's theorem and quasi-similarity.
Integral Equations and Operator Theory,
Vol. 39,
Issue. 2,
p.
214.
Bong Jung, Il
Ko, Eungil
and
Pearcy, Carl
2001.
Spectral pictures of Aluthge transforms of operators.
Integral Equations and Operator Theory,
Vol. 40,
Issue. 1,
p.
52.
Jeon, In-Ho
Kim, Se-Hee
Ko, Eun-Gil
and
Park, Ji-Eun
2002.
ON POSITIVE-NORMAL OPERATORS.
Bulletin of the Korean Mathematical Society,
Vol. 39,
Issue. 1,
p.
33.
DUGGAL, BHAGWATI P.
and
JEON, IN-HO
2005.
REMARKS ON SPECTRAL PROPERTIES OF p-HYPONORMAL AND LOG-HYPONORMAL OPERATORS.
Bulletin of the Korean Mathematical Society,
Vol. 42,
Issue. 3,
p.
543.
Kim, An-Hyun
and
Kwon, Eun-Young
2006.
SPECTRAL CONTINUITY OF ESSENTIALLY p-HYPONORMAL OPERATORS.
Bulletin of the Korean Mathematical Society,
Vol. 43,
Issue. 2,
p.
389.
Ko, Eungil
2007.
p-Quasihyponormal operators have scalar extensions of order 6.
Journal of Mathematical Analysis and Applications,
Vol. 330,
Issue. 1,
p.
80.
IRENE MARY, J. STELLA
and
PANAYAPPAN, S.
2008.
WEYL'S THEOREM FOR CLASSA(k) OPERATORS.
Glasgow Mathematical Journal,
Vol. 50,
Issue. 1,
p.
39.
Senthilkumar, D.
Naik, P. Maheswari
and
Sivakumar, N.
2012.
GENERALIZED WEYL'S THEOREM FOR ALGEBRAICALLY <TEX>$k$</TEX>-QUASI-PARANORMAL OPERATORS.
Journal of the Chungcheong Mathematical Society ,
Vol. 25,
Issue. 4,
p.
655.
Mecheri, Salah
and
Braha, Naim L.
2020.
Polaroid operators and Weyl type theorems.
Asian-European Journal of Mathematics,
Vol. 13,
Issue. 07,
p.
2050123.
Yi, Jialu
and
Cao, Xiaohong
2025.
A new criteria for two Weyl’s type theorems.
Filomat,
Vol. 39,
Issue. 11,
p.
3537.
Dana, Mansour
Kousari, Fateme
and
Yousefi, Ramesh
2025.
On D-hyponormal operators.
Journal of Inequalities and Applications,
Vol. 2025,
Issue. 1,

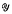 of ℋ, the norm closure of
of ℋ, the norm closure of 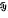 . The Weyl spectrum ω(
. The Weyl spectrum ω(