Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Choo, Koo-Guan
1980.
Whitehead groups of semidirect products of free groups II.
Glasgow Mathematical Journal,
Vol. 21,
Issue. 1,
p.
71.


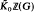 . Let α be an automorphism of
. Let α be an automorphism of 