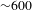1 Introduction
In recent years, petawatt class lasers operating at ultra-high intensities to target have become relatively common in national laboratories and even university environments[Reference Danson, Hillier, Hopps and Neely1]. The pulse fidelity of these lasers is difficult to quantify in terms of focal spot distribution, pulse duration, pulse shape and temporal contrast, leading to problems in understanding the physics of the interactions. At intensities to target of
![]() ${>}10^{21}~\text{W}\cdot \text{cm}^{-2}$
and with solid target interactions it is particularly important to understand the contrast of the pulse, and ideally have a ‘clean’ pulse to begin with. The origins of pre-pulse in a large-scale facility such as Orion are multiple: from satellite pulses within the oscillator, parametric fluorescence in the pre-amplifiers, amplified spontaneous emission (ASE) in the main amplifier chain, etc. By converting the output pulse on Orion to the second harmonic any pre-pulses associated with the main laser pulse are suppressed.
${>}10^{21}~\text{W}\cdot \text{cm}^{-2}$
and with solid target interactions it is particularly important to understand the contrast of the pulse, and ideally have a ‘clean’ pulse to begin with. The origins of pre-pulse in a large-scale facility such as Orion are multiple: from satellite pulses within the oscillator, parametric fluorescence in the pre-amplifiers, amplified spontaneous emission (ASE) in the main amplifier chain, etc. By converting the output pulse on Orion to the second harmonic any pre-pulses associated with the main laser pulse are suppressed.
The Orion laser facility at the Atomic Weapons Establishment (AWE) has been operating since 2013[Reference Hopps, Danson, Duffield, Egan, Elsmere, Girling, Harvey, Hillier, Norman, Parker, Treadwell, Winter and Bett2]. Orion consists of twelve primary beamlines, ten of which are ‘long pulse’ with a controllable pulse duration and temporal profile in the range of 0.1–10 ns. The remaining two beamlines are ‘short pulse’ with a sub-picosecond pulse duration. These two sets of beamlines are used in combination to achieve the conditions necessary for high energy and high density plasma physics experiments.
The short-pulse architecture is based on chirped pulse amplification[Reference Strickland and Mourou3] whereby the pulse is temporally stretched, amplified and finally compressed. A schematic representation of the Orion short-pulse beamlines is shown in Figure 1. The short-pulse beamlines start as a common Ti:sapphire oscillator producing an 80 MHz pulse train of 160 fs pulses, with 3 nJ pulse energy, centred at 1054 nm. The oscillator pulses enter a short-pulse parametric amplifier (SPOPA)[Reference Hillier, Elsmere, Girling, Hopps, Hussey, Parker, Treadwell, Winter and Bett4], which selects a single pulse at 10 Hz, stretches it to 1 ps and amplifies the pulse energy to
![]() $30~\unicode[STIX]{x03BC}\text{J}$
. The SPOPA pulse is split to seed the two separate short-pulse beamlines. Each pulse then enters an Offner triplet stretcher, which stretches the pulse to 6 ns. Next, the pulse is amplified in a three-stage lithium triborate optical parametric amplifier (OPA)[Reference Girling, Parker, Hussey and Hopps5], which increases the pulse energy to 150 mJ while maintaining the bandwidth of the seed pulse. The OPA output enters a double passed pair of phosphate (LHG-8) and silicate (ED-2) glass rod amplifiers, which amplify the pulse to 1 J, and is further amplified in a series of increasing aperture Nd-doped Schott LG770 disk amplifiers. The resulting pulse has an energy of up to 700 J in a 600 mm diameter beam. This is then compressed in time using a pair of 940 mm diameter gold-coated diffraction gratings. The resulting compressed pulse is 500 J with a pulse duration of 500 fs (1 PW). Finally, the pulse is focused onto target using an off-axis parabola. A wavefront sensor (Imagine Optic HASO3) and a 63-element monomorph deformable mirror (DFM) are used to compensate for aberrations present in the beamline. To obtain optimum compression, it is desirable to minimize the wavefront error incident onto the second compressor grating; therefore the DFM is used to minimize the aberrations at this location. The off-axis parabola can then be used to compensate for focus and astigmatism arising from the second grating and any subsequent optics. This is achieved by imaging the focal spot at the target chamber centre (TCC) using a microscope camera. Under near diffraction limited conditions this pulse can then be focused onto target to a spot
$30~\unicode[STIX]{x03BC}\text{J}$
. The SPOPA pulse is split to seed the two separate short-pulse beamlines. Each pulse then enters an Offner triplet stretcher, which stretches the pulse to 6 ns. Next, the pulse is amplified in a three-stage lithium triborate optical parametric amplifier (OPA)[Reference Girling, Parker, Hussey and Hopps5], which increases the pulse energy to 150 mJ while maintaining the bandwidth of the seed pulse. The OPA output enters a double passed pair of phosphate (LHG-8) and silicate (ED-2) glass rod amplifiers, which amplify the pulse to 1 J, and is further amplified in a series of increasing aperture Nd-doped Schott LG770 disk amplifiers. The resulting pulse has an energy of up to 700 J in a 600 mm diameter beam. This is then compressed in time using a pair of 940 mm diameter gold-coated diffraction gratings. The resulting compressed pulse is 500 J with a pulse duration of 500 fs (1 PW). Finally, the pulse is focused onto target using an off-axis parabola. A wavefront sensor (Imagine Optic HASO3) and a 63-element monomorph deformable mirror (DFM) are used to compensate for aberrations present in the beamline. To obtain optimum compression, it is desirable to minimize the wavefront error incident onto the second compressor grating; therefore the DFM is used to minimize the aberrations at this location. The off-axis parabola can then be used to compensate for focus and astigmatism arising from the second grating and any subsequent optics. This is achieved by imaging the focal spot at the target chamber centre (TCC) using a microscope camera. Under near diffraction limited conditions this pulse can then be focused onto target to a spot
![]() ${<}10~\unicode[STIX]{x03BC}\text{m}$
in diameter, resulting in an intensity of
${<}10~\unicode[STIX]{x03BC}\text{m}$
in diameter, resulting in an intensity of
![]() ${>}10^{21}~\text{W}\cdot \text{cm}^{-2}$
.
${>}10^{21}~\text{W}\cdot \text{cm}^{-2}$
.
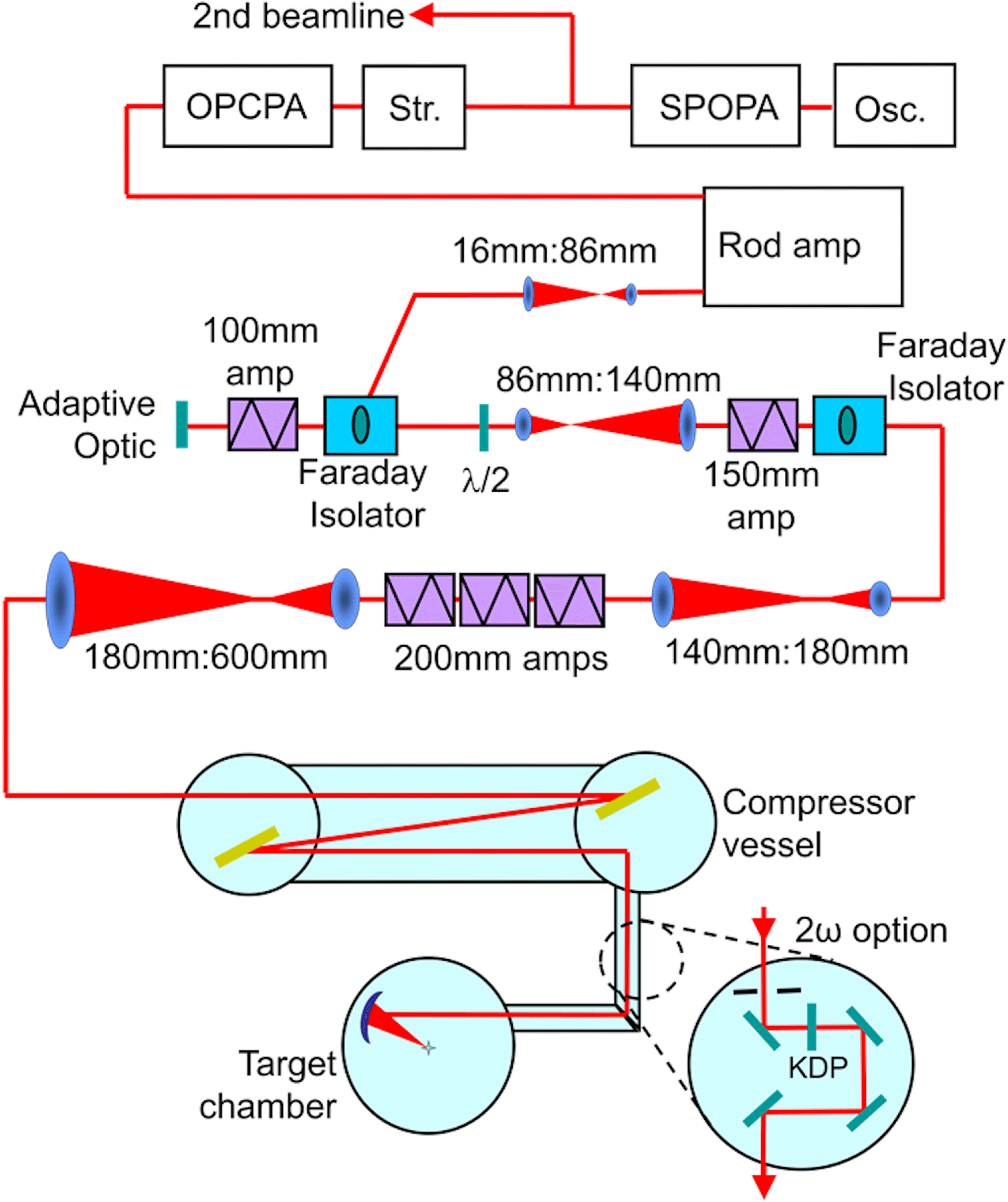
Figure 1. Schematic representation of a short-pulse beamline.
A key capability of the Orion facility is the ability to frequency-double one of the short-pulse beamlines. The frequency doubling achieves two advantageous conditions. First, the wavelength enables a different regime of laser–plasma interactions to be studied. Second, and more importantly, it provides an increase in the temporal contrast of the laser pulse. Previous investigations of type-I frequency doubling of femtosecond and picosecond laser pulses from Nd:glass[Reference Chien, Korn, Coe, Squier and Mourou6–Reference Hillier, Girling, Kopec, Hopps, Nolan and Winter10] and Ti:sapphire[Reference Krylov, Rebane, Kalintsev, Schwoerer and Wild11, Reference Aoyama, Harimoto, Ma, Akahane and Yamakawa12] lasers have been performed at smaller apertures, lower energies and/or lower intensities. Frequency doubling has been demonstrated to improve the contrast ratio (the relative intensity of the ASE pedestal to the main pulse) of the Orion beamline from
![]() $10^{7}$
to
$10^{7}$
to
![]() $10^{14}$
[Reference Hillier, Danson, Duffield, Egan, Elsmere, Girling, Harvey, Hopps, Norman, Parker, Treadwell, Winter and Bett13]. Subsequently, the SPOPA upgrade enabled a further improvement of the contrast ratio to
$10^{14}$
[Reference Hillier, Danson, Duffield, Egan, Elsmere, Girling, Harvey, Hopps, Norman, Parker, Treadwell, Winter and Bett13]. Subsequently, the SPOPA upgrade enabled a further improvement of the contrast ratio to
![]() $10^{18}$
[Reference Hillier, Elsmere, Girling, Hopps, Hussey, Parker, Treadwell, Winter and Bett4].
$10^{18}$
[Reference Hillier, Elsmere, Girling, Hopps, Hussey, Parker, Treadwell, Winter and Bett4].
Frequency doubling on Orion is achieved by passing the amplified compressed pulse through a 3 mm thick potassium dihydrogen phosphate crystal cut for type-I frequency doubling. Unfortunately, it is not currently possible to obtain a 3 mm crystal at the full 600 mm beam diameter with the required transmitted wavefront quality; the largest possible during facility construction was a 325 mm circular aperture. It was necessary therefore to reduce the beam to 300 mm using a segmented absorbing glass apodizer, prior to the conversion crystal. This reduced the maximum pulse energy of the short pulse from 500 J (1 PW) at 1054 nm to 100 J (200 TW) at 527 nm. The experiments carried out in the second harmonic (
![]() $2\unicode[STIX]{x1D714}$
) proved very successful[Reference Hoarty, Allan, James, Brown, Hobbs, Hill, Harris, Morton, Brookes, Shepherd, Dunn, Chen, Von Marley, Beiersdorfer, Brown and Emig14] and drove the desire to explore the options for increasing the available energy.
$2\unicode[STIX]{x1D714}$
) proved very successful[Reference Hoarty, Allan, James, Brown, Hobbs, Hill, Harris, Morton, Brookes, Shepherd, Dunn, Chen, Von Marley, Beiersdorfer, Brown and Emig14] and drove the desire to explore the options for increasing the available energy.
2 Enhanced second-harmonic capability design
The modelled spatial profile of the first-harmonic (
![]() $1\unicode[STIX]{x1D714}$
) light is shown in Figure 2(a); this is a 600 mm diameter beam that is laterally dispersed by compression using a grating pair and also partially apodized by the final turning mirror in the compressor vessel. The modelled transmitted spatial profile of the 300 mm apodized beam used in the original design is shown in Figure 2(b). A calculated transmission of 28% of the
$1\unicode[STIX]{x1D714}$
) light is shown in Figure 2(a); this is a 600 mm diameter beam that is laterally dispersed by compression using a grating pair and also partially apodized by the final turning mirror in the compressor vessel. The modelled transmitted spatial profile of the 300 mm apodized beam used in the original design is shown in Figure 2(b). A calculated transmission of 28% of the
![]() $1\unicode[STIX]{x1D714}$
light allows a baseline for comparison for assessing potential designs. Discussions with crystal manufacturers suggested that a 500 mm circular aperture crystal may be possible; this is shown in Figure 2(c). The 500 mm aperture crystal gives an expected transmission of 71%, an increase of 2.5 times over the original design. A square 320 mm crystal was also evaluated due to ease of manufacture and integration into the current beamline. This gave a modest increase of 1.2 times the energy with a transmission of 34%. Finally, the use of twin smaller tiled crystals was also considered as shown in Figures 2(e) and 2(f). These designs are both stacked vertically as this maximizes the transmission due to the laterally dispersed beam. The use of twin 325 mm circular and 320 mm square crystals gives a transmission of 50% and 60%, respectively (an increase of 1.8 and 2.1 times over the original design).
$1\unicode[STIX]{x1D714}$
light allows a baseline for comparison for assessing potential designs. Discussions with crystal manufacturers suggested that a 500 mm circular aperture crystal may be possible; this is shown in Figure 2(c). The 500 mm aperture crystal gives an expected transmission of 71%, an increase of 2.5 times over the original design. A square 320 mm crystal was also evaluated due to ease of manufacture and integration into the current beamline. This gave a modest increase of 1.2 times the energy with a transmission of 34%. Finally, the use of twin smaller tiled crystals was also considered as shown in Figures 2(e) and 2(f). These designs are both stacked vertically as this maximizes the transmission due to the laterally dispersed beam. The use of twin 325 mm circular and 320 mm square crystals gives a transmission of 50% and 60%, respectively (an increase of 1.8 and 2.1 times over the original design).

Figure 2. Comparison of the modelled spatial profile and expected transmission of the considered conversion crystal designs: (a) unconverted spatial profile, (b) original 325 mm circular, (c) 500 mm circular, (d) 320 mm square, (e) dual 325 mm circular, (f) dual 320 mm square.
Evaluating the options showed that the 500 mm large aperture crystal and the twin 320 mm square crystal schemes gave the greatest improvement to the
![]() $2\unicode[STIX]{x1D714}$
energy. For the large aperture option the 500 mm crystal posed a significant manufacturing risk. In addition to this there were concerns that the larger dichroic mirrors required for this design would not fit within the existing chamber and would be prohibitively expensive to implement. For the twin crystal option the greatest challenge is ensuring that the two emerging beamlets can be spatially and temporally overlapped on target. This would require the use of two separate motorized mirrors, vertically stacked (‘double deck’), each capable of tilt and piston control. Although the mirror mounts would need to be redesigned, it was possible to reuse the existing dichroic mirrors used in the frequency conversion process. Considering the relative risk, complexity and cost it was decided to proceed with the twin square crystal option.
$2\unicode[STIX]{x1D714}$
energy. For the large aperture option the 500 mm crystal posed a significant manufacturing risk. In addition to this there were concerns that the larger dichroic mirrors required for this design would not fit within the existing chamber and would be prohibitively expensive to implement. For the twin crystal option the greatest challenge is ensuring that the two emerging beamlets can be spatially and temporally overlapped on target. This would require the use of two separate motorized mirrors, vertically stacked (‘double deck’), each capable of tilt and piston control. Although the mirror mounts would need to be redesigned, it was possible to reuse the existing dichroic mirrors used in the frequency conversion process. Considering the relative risk, complexity and cost it was decided to proceed with the twin square crystal option.
The final engineering design for the twin beamlet frequency conversion chamber is shown in Figure 3. The incoming 600 mm beam is apodized into two square 300 mm beamlets using absorbing glass. Additional glass at
![]() $45^{\circ }$
at the corners reduces local intensity spikes downstream. To maximize transmission, the vertical separation of the two beamlets is kept to a minimum (45 mm), with the crystal mounts overlapped. The two beamlets are then reflected off a ‘double-deck’ dichroic mirror (MR1 in Figure 3), which is reflective at
$45^{\circ }$
at the corners reduces local intensity spikes downstream. To maximize transmission, the vertical separation of the two beamlets is kept to a minimum (45 mm), with the crystal mounts overlapped. The two beamlets are then reflected off a ‘double-deck’ dichroic mirror (MR1 in Figure 3), which is reflective at
![]() $1\unicode[STIX]{x1D714}$
but transmits at
$1\unicode[STIX]{x1D714}$
but transmits at
![]() $2\unicode[STIX]{x1D714}$
. A 527 nm alignment beam is injected through the back of this mirror and pointed coaxially with the incoming unconverted beam using a motorized insertable diagnostic mirror. The beamlets then pass through the twin conversion crystals, which are independently adjustable in the fast axes to enable angle tuning to realize maximum conversion efficiency. The
$2\unicode[STIX]{x1D714}$
. A 527 nm alignment beam is injected through the back of this mirror and pointed coaxially with the incoming unconverted beam using a motorized insertable diagnostic mirror. The beamlets then pass through the twin conversion crystals, which are independently adjustable in the fast axes to enable angle tuning to realize maximum conversion efficiency. The
![]() $2\unicode[STIX]{x1D714}$
beamlets then reflect off a series of three more ‘double-deck’ dichroic mirrors (MR2-4); these are now reflective at
$2\unicode[STIX]{x1D714}$
beamlets then reflect off a series of three more ‘double-deck’ dichroic mirrors (MR2-4); these are now reflective at
![]() $2\unicode[STIX]{x1D714}$
but transmit at
$2\unicode[STIX]{x1D714}$
but transmit at
![]() $1\unicode[STIX]{x1D714}$
to minimize the unconverted light that reaches the target. The majority of the unconverted light is dumped into the absorbing glass behind MR2. The light leaking through MR3 emerges through the existing chamber port and is used to diagnose the
$1\unicode[STIX]{x1D714}$
to minimize the unconverted light that reaches the target. The majority of the unconverted light is dumped into the absorbing glass behind MR2. The light leaking through MR3 emerges through the existing chamber port and is used to diagnose the
![]() $2\unicode[STIX]{x1D714}$
performance. The diagnostic port was only designed to be large enough to accept the original 300 mm diameter beam and therefore significantly apodize the twin beamlets to the diagnostics.
$2\unicode[STIX]{x1D714}$
performance. The diagnostic port was only designed to be large enough to accept the original 300 mm diameter beam and therefore significantly apodize the twin beamlets to the diagnostics.

Figure 3. Frequency conversion chamber incorporating the twin crystal and ‘double-deck’ vertical dichroic mirrors.
The second mirror mount is motorized to spatially and temporally overlap the two beamlets on target. The required angular resolution of the mounts is approximately
![]() $5~\unicode[STIX]{x03BC}\text{rad}$
. In addition, the path length of the two beamlets must be matched to within a fraction of a wavelength if the beamlets are to combine coherently and act as a single beam when focused. Therefore the mirrors must be translated, without introducing additional tilt, with a resolution of around 100 nm. To assess the performance of the new mirror mount an autocollimator was used to measure the pointing as a function of actuator position, as shown in Figure 4. A hysteresis of the order of
$5~\unicode[STIX]{x03BC}\text{rad}$
. In addition, the path length of the two beamlets must be matched to within a fraction of a wavelength if the beamlets are to combine coherently and act as a single beam when focused. Therefore the mirrors must be translated, without introducing additional tilt, with a resolution of around 100 nm. To assess the performance of the new mirror mount an autocollimator was used to measure the pointing as a function of actuator position, as shown in Figure 4. A hysteresis of the order of
![]() $5~\unicode[STIX]{x03BC}\text{rad}$
was measured; this could be a problem in practice as the individual actuators must act together to produce pure azimuth, elevation and piston motions. By modifying the software within the motion controller, in particular the actuator feedback loop parameters and the backlash compensation pre-sets, it was possible to almost completely remove the hysteresis as shown in Figure 4(b).
$5~\unicode[STIX]{x03BC}\text{rad}$
was measured; this could be a problem in practice as the individual actuators must act together to produce pure azimuth, elevation and piston motions. By modifying the software within the motion controller, in particular the actuator feedback loop parameters and the backlash compensation pre-sets, it was possible to almost completely remove the hysteresis as shown in Figure 4(b).

Figure 4. Measured hysteresis of an actuator driven mirror mount (a) before and (b) after software compensation.
The final focusing optic for the short-pulse beamline is an off-axis parabolic mirror mounted on a motorized hexapod. For
![]() $1\unicode[STIX]{x1D714}$
operation this is an
$1\unicode[STIX]{x1D714}$
operation this is an
![]() $f/3$
720 mm diameter parabolic mirror coated for use at 1054 nm. The original
$f/3$
720 mm diameter parabolic mirror coated for use at 1054 nm. The original
![]() $2\unicode[STIX]{x1D714}$
design utilized an
$2\unicode[STIX]{x1D714}$
design utilized an
![]() $f/6$
360 mm diameter dichroic mirror coated for use at 527 nm; this was mounted onto the same hexapod using an aluminium adaptor ring. For the new twin beamlet design, an
$f/6$
360 mm diameter dichroic mirror coated for use at 527 nm; this was mounted onto the same hexapod using an aluminium adaptor ring. For the new twin beamlet design, an
![]() $f/3$
720 mm (
$f/3$
720 mm (
![]() ${\sim}f/6$
for each beamlet) dichroic parabolic mirror coated for 527 nm operation is used.
${\sim}f/6$
for each beamlet) dichroic parabolic mirror coated for 527 nm operation is used.
3 Enhanced second-harmonic performance
The original frequency conversion components were removed from the vacuum chamber and replaced by the new twin beamlet design. A microscope camera was used to image the focused beams at the TCC. Pulses from the OPA were propagated along the beamline and through the frequency conversion chamber. There is sufficient intensity for the frequency-doubled pulses to be visible when focused by the parabola at the TCC. This camera was then used to angle-tune the frequency conversion crystals for maximum conversion efficiency. The top dichroic mirror on the second ‘double-deck’ mount was then tilted to bring the two beamlets together near focus. A piston scan was then performed using this mirror to scan its path length relative to the lower deck. The pulse coherence length of
![]() ${\sim}0.5$
ps gave an interaction length of approximately
${\sim}0.5$
ps gave an interaction length of approximately
![]() $150~\unicode[STIX]{x03BC}\text{m}$
over which interference between the two beamlets was visible. For this measurement an apodizer was placed in the near-field to sub-aperture each beamlet to mitigate the imperfect focal spot profile and therefore improve the interference fringe clarity, as shown in Figure 5(a). The top mirror was then positioned in the centre of this range, where the fringe contrast was the greatest, so as to synchronize the two beamlets. An imaging camera was also used to measure the near-field pattern of the two beamlets incident on the parabola. Figure 5(b) shows a composite image of the two
$150~\unicode[STIX]{x03BC}\text{m}$
over which interference between the two beamlets was visible. For this measurement an apodizer was placed in the near-field to sub-aperture each beamlet to mitigate the imperfect focal spot profile and therefore improve the interference fringe clarity, as shown in Figure 5(a). The top mirror was then positioned in the centre of this range, where the fringe contrast was the greatest, so as to synchronize the two beamlets. An imaging camera was also used to measure the near-field pattern of the two beamlets incident on the parabola. Figure 5(b) shows a composite image of the two
![]() $2\unicode[STIX]{x1D714}$
beamlets as well as the compressed
$2\unicode[STIX]{x1D714}$
beamlets as well as the compressed
![]() $1\unicode[STIX]{x1D714}$
beam.
$1\unicode[STIX]{x1D714}$
beam.
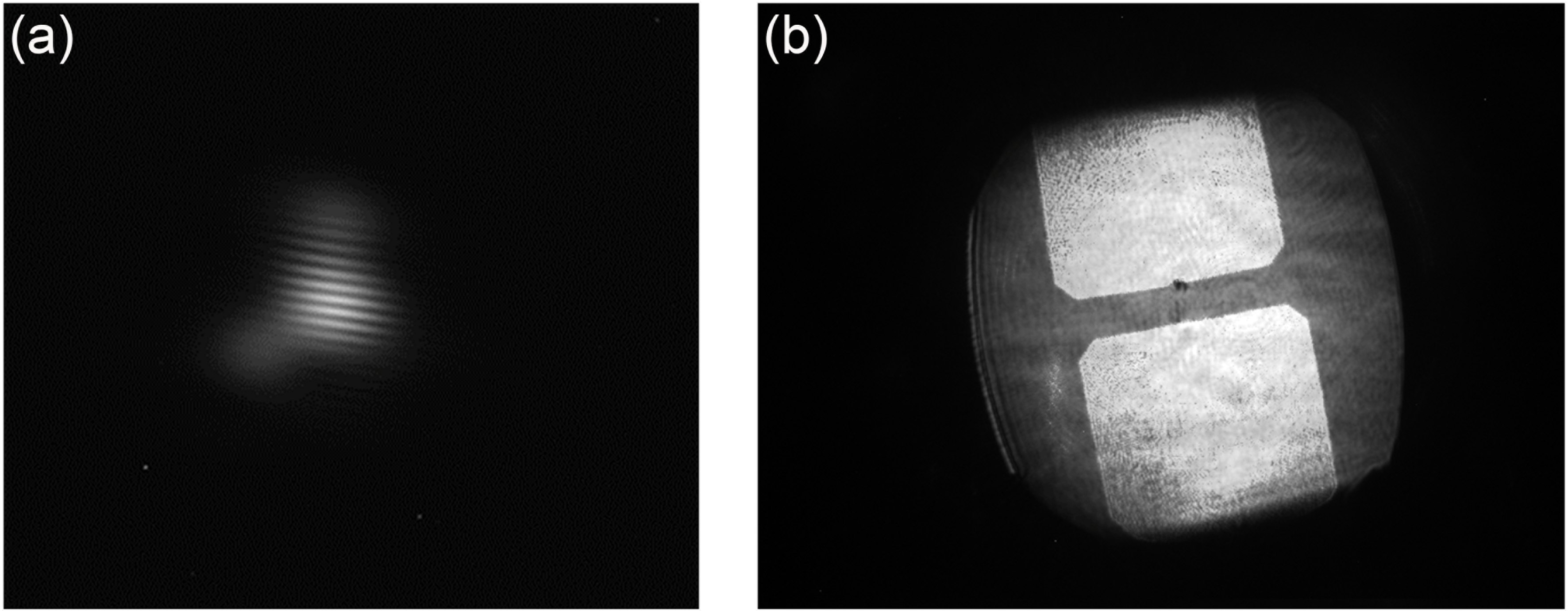
Figure 5. (a) Interference pattern created by temporally overlapping the two sub-aperture
![]() $2\unicode[STIX]{x1D714}$
beamlets. (b) Composite image of the spatial profiles of the compressed
$2\unicode[STIX]{x1D714}$
beamlets. (b) Composite image of the spatial profiles of the compressed
![]() $1\unicode[STIX]{x1D714}$
beam and the two
$1\unicode[STIX]{x1D714}$
beam and the two
![]() $2\unicode[STIX]{x1D714}$
beamlets. The
$2\unicode[STIX]{x1D714}$
beamlets. The
![]() $1\unicode[STIX]{x1D714}$
beam is measured on a diagnostic station after the second compressor grating. The
$1\unicode[STIX]{x1D714}$
beam is measured on a diagnostic station after the second compressor grating. The
![]() $2\unicode[STIX]{x1D714}$
profile was measured using an imaging camera positioned at the TCC.
$2\unicode[STIX]{x1D714}$
profile was measured using an imaging camera positioned at the TCC.

Figure 6. X-ray spot images. (a) At best focus, spot
![]() $\text{size}=30~\unicode[STIX]{x03BC}\text{m}$
. (b) Defocus of
$\text{size}=30~\unicode[STIX]{x03BC}\text{m}$
. (b) Defocus of
![]() $600~\unicode[STIX]{x03BC}\text{m}$
, sub-apertures overlapped, spot
$600~\unicode[STIX]{x03BC}\text{m}$
, sub-apertures overlapped, spot
![]() $\text{size}=90~\unicode[STIX]{x03BC}\text{m}$
.
$\text{size}=90~\unicode[STIX]{x03BC}\text{m}$
.
The microscope camera was then used to optimize the focal spot of the two beamlets using the off-axis parabola as described previously. Unfortunately, the four reused dichroic turning mirrors had developed a significant defocus aberration since their initial installation (total of
![]() $1.2~\unicode[STIX]{x03BC}\text{m}$
). Although this could be adequately compensated for in the case of the single beam, it posed an additional challenge for the dual beamlet design. A solution was to share the affected mirrors between the two beamlets. The individual weakly defocused beamlets could then be optimized through the application of tilt using the final turning mirrors to bring the centres of the apparent defocus wavefront errors together such that they could be largely compensated for by the positioning of the off-axis parabola. The residual aberrations from these mirrors, together with those of the second diffraction grating, are the dominant sources of wavefront error for the focal spots. The remaining optical components, including the new turning mirrors, off-axis parabola and the two frequency conversion crystals, impart a negligible effect. Through optimization of the off-axis parabola position it was possible to achieve a focal spot of
$1.2~\unicode[STIX]{x03BC}\text{m}$
). Although this could be adequately compensated for in the case of the single beam, it posed an additional challenge for the dual beamlet design. A solution was to share the affected mirrors between the two beamlets. The individual weakly defocused beamlets could then be optimized through the application of tilt using the final turning mirrors to bring the centres of the apparent defocus wavefront errors together such that they could be largely compensated for by the positioning of the off-axis parabola. The residual aberrations from these mirrors, together with those of the second diffraction grating, are the dominant sources of wavefront error for the focal spots. The remaining optical components, including the new turning mirrors, off-axis parabola and the two frequency conversion crystals, impart a negligible effect. Through optimization of the off-axis parabola position it was possible to achieve a focal spot of
![]() ${<}15~\unicode[STIX]{x03BC}\text{m}$
, correlating to less than twice the diffraction limit. A scheme to further optimize the focal spots using a wavefront sensor at the TCC is currently under development.
${<}15~\unicode[STIX]{x03BC}\text{m}$
, correlating to less than twice the diffraction limit. A scheme to further optimize the focal spots using a wavefront sensor at the TCC is currently under development.
A series of test shots were then carried out to measure the
![]() $2\unicode[STIX]{x1D714}$
performance. A direct measurement of the pulse energy of the two beamlets was not feasible as the conversion chamber and target chamber are both required to be at vacuum for shot firing operations. A method to calculate the total energy in the two beamlets is used based on a cross calibration using the
$2\unicode[STIX]{x1D714}$
performance. A direct measurement of the pulse energy of the two beamlets was not feasible as the conversion chamber and target chamber are both required to be at vacuum for shot firing operations. A method to calculate the total energy in the two beamlets is used based on a cross calibration using the
![]() $2\unicode[STIX]{x1D714}$
diagnostic station. This diagnostic station measures a sub-aperture of the two beamlets and uses a common calorimeter to measure both beamlets simultaneously. Comparison of this energetic data with the original
$2\unicode[STIX]{x1D714}$
diagnostic station. This diagnostic station measures a sub-aperture of the two beamlets and uses a common calorimeter to measure both beamlets simultaneously. Comparison of this energetic data with the original
![]() $2\unicode[STIX]{x1D714}$
data (where the diagnostic beam was the full aperture of the main
$2\unicode[STIX]{x1D714}$
data (where the diagnostic beam was the full aperture of the main
![]() $2\unicode[STIX]{x1D714}$
beam) allows for the extrapolation of the energy in the new
$2\unicode[STIX]{x1D714}$
beam) allows for the extrapolation of the energy in the new
![]() $2\unicode[STIX]{x1D714}$
configuration. The maximum
$2\unicode[STIX]{x1D714}$
configuration. The maximum
![]() $2\unicode[STIX]{x1D714}$
energy measured on a shot with this technique is 210 J. As the pulse duration of the
$2\unicode[STIX]{x1D714}$
energy measured on a shot with this technique is 210 J. As the pulse duration of the
![]() $1\unicode[STIX]{x1D714}$
beam (prior to frequency conversion) is typically measured to be of the order of 500 fs, this relates to a
$1\unicode[STIX]{x1D714}$
beam (prior to frequency conversion) is typically measured to be of the order of 500 fs, this relates to a
![]() $2\unicode[STIX]{x1D714}$
power of approximately 400 TW.
$2\unicode[STIX]{x1D714}$
power of approximately 400 TW.
This enhanced capability is now being utilized on full energy plasma physics experiments. Figure 6 shows X-ray images taken with a pinhole camera on a shot. The X-ray emitting spot size measured at the best focus is
![]() $30~\unicode[STIX]{x03BC}\text{m}$
. This is larger than the spot measured with the microscope camera (
$30~\unicode[STIX]{x03BC}\text{m}$
. This is larger than the spot measured with the microscope camera (
![]() ${<}15~\unicode[STIX]{x03BC}\text{m}$
), but is consistent with simulations of X-ray spot enlargement due to electron reflux[Reference Hoarty, Sircombe, Beiersdorfer, Brown, Hill, Hobbs, James, Morton, Hill, Jeffery, Harris, Shepherd, Marley, Magee, Emig, Nilsen, Chung, Lee and Rose15], and is comparable to that achieved before the upgrade. Also shown is a defocused spot. When the parabola is defocused, the beamlets begin to separate as the beam transforms into the near-field. This can be prevented by giving the beamlets a relative tilt to overlap the defocused spots. Although this produces high-frequency interference fringes at the laser wavelength, these do not appear in the X-rays produced.
${<}15~\unicode[STIX]{x03BC}\text{m}$
), but is consistent with simulations of X-ray spot enlargement due to electron reflux[Reference Hoarty, Sircombe, Beiersdorfer, Brown, Hill, Hobbs, James, Morton, Hill, Jeffery, Harris, Shepherd, Marley, Magee, Emig, Nilsen, Chung, Lee and Rose15], and is comparable to that achieved before the upgrade. Also shown is a defocused spot. When the parabola is defocused, the beamlets begin to separate as the beam transforms into the near-field. This can be prevented by giving the beamlets a relative tilt to overlap the defocused spots. Although this produces high-frequency interference fringes at the laser wavelength, these do not appear in the X-rays produced.
4 Conclusion
The second-harmonic performance of one of the Orion short-pulse beamlines has successfully been enhanced. The change in design from a single 300 mm circular beam to twin 300 mm square beamlets has resulted in a 2.1 times increase in achievable
![]() $2\unicode[STIX]{x1D714}$
energy. The capability of coherently recombining these two beamlets on target has been demonstrated.
$2\unicode[STIX]{x1D714}$
energy. The capability of coherently recombining these two beamlets on target has been demonstrated.
The upgraded performance has been utilized for plasma physics experiments. The increased
![]() $2\unicode[STIX]{x1D714}$
energy is able to heat through more material, enabling experiments at higher density than previously. Also, the ability to heat larger volumes of material reduces the temperature gradients within a prepared sample of high energy density material, leading to more accurate results. The maximum
$2\unicode[STIX]{x1D714}$
energy is able to heat through more material, enabling experiments at higher density than previously. Also, the ability to heat larger volumes of material reduces the temperature gradients within a prepared sample of high energy density material, leading to more accurate results. The maximum
![]() $2\unicode[STIX]{x1D714}$
pulse energy of 210 J demonstrated in these experiments, with a typical pulse duration of 500 fs, corresponds to a total power deliverable to target of approximately 400 TW.
$2\unicode[STIX]{x1D714}$
pulse energy of 210 J demonstrated in these experiments, with a typical pulse duration of 500 fs, corresponds to a total power deliverable to target of approximately 400 TW.