1. Introduction
This review paper has been written with the assumption that the readers are primarily scientists well aware of both the principles of inertial confinement fusion and of a laser fusion power plant design.
Laser performance has increased greatly since the very beginning in 1960 when the laser was discovered (it was more a discovery than an invention, a solution looking for a problem[Reference Hecht1]). Each year sees new improvements and there are many papers that discuss the future of lasers. Diode-pumped solid-state lasers (DPSSLs) and krypton fluoride (KrF) lasers both have the potential efficiency and repetition rate required for power production[Reference Bodner, Schmitt and Sethian2], and these laser concepts have been identified and studied in detail during the HAPL Program[3].
The real advantage of a laser driver compared with other drivers is its ability to provide a high quality focal spot on a target. It is not easy to design the driver baseline because, first, there are too many different parameters to deal with and, second, heat generation in solid-state media has always been recognized as a limiting feature, because at high repetition rate, the quality of the focal spot depends on the beam wave-front distortion[Reference Emmett, Krupke and Sooy4]. This is not true for KrF lasers because thermal management is not the limiting factor[Reference Bodner, Schmitt and Sethian2]. After more than fifty years of development, it is clear that the solution looking for a problem is finally encountering problems when reaching an average power in the tens of kW range.
Nevertheless, many improvements have been made in solid-state lasers when using ytterbium (Yb) instead of neodymium (Nd)[Reference Krupke5], considering cryogenic cooling[Reference Brown6] and the use of ceramic gain media instead of single crystals[Reference Meier7, Reference Le Garrec, Bourdet and Cardinali8].
Flashlamp-pumped fusion lasers are still in the race; they have a low efficiency (1.5%–2%) but can access high beam quality and high harmonic generation. Nd-doped glass lasers (Nd:glass) are by far the most widely used type of driver in inertial confinement fusion both in existing facilities and in the largest one that is being built: the National Ignition Facility (NIF) in the USA[Reference Moses and Wuest9] and the Laser Mégajoule (LMJ) in France[Reference Ebrardt and Chaput10]. There are several good reasons for the preponderance of this type of laser material but the most important is its availability at large size. The total efficiency of NIF or LMJ can be assessed in the range of 0.5%–1%. 0.66% efficiency has been published for NIF[Reference Caird, Agrawal, Bayramian, Beach, Britten, Chen, Cross, Ebbers, Erlandson, Feit, Freitas, Ghosh, Hæfner, Homœlle, Ladran, Latkowski, Molander, Murray, Rubenchik, Schaffers, Siders, Stappaerts, Sutton, Telford, Trenholme and Barty11].
Since the 1990s, several programmes involving DPSSLs have been launched in the USA, Europe, and Japan. At that time, the goal was already to reach kW average power level and the magic set of parameters was 100 J ns pulses at 10 Hz[12].

Figure 1. Laser pulses for (a) fast ignition and (b) shock ignition. In both cases, the compression pulse is preceded by an adiabatic shaping picket (of 100–200 ps duration) from Ref. [Reference Le Garrec, Atzeni, Batani, Gizzi, Ribeyre, Schurtz, Schiavi, Ertel, Collier, Edwards, Perlado, Honrubia and Rus22].
Then, thanks to the European Strategic Forum Initiative, two programmes were able to emerge: ELI (Extreme Light Infrastructure) and HiPER (the European High Power laser Energy Research facility)[13, 14]. The main objective of ELI is to deliver ultra-short high energy pulses to provide focused intensities attaining more than ![]() $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}10^{22}\ {\rm W\ cm}^{-2}$ for scientific applications, while HiPER is dedicated to demonstrating laser-driven fusion as a future energy source. On the ‘laser’ side, HiPER’s objective is to identify the least expensive and most useful driver but not to preclude any alternative laser design that can make the facility more flexible. Before the final facility design,a major challenge for HiPER will be to enable rep-rated laser operation of around 10 Hz to demonstrate fusion in a burst mode.
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}10^{22}\ {\rm W\ cm}^{-2}$ for scientific applications, while HiPER is dedicated to demonstrating laser-driven fusion as a future energy source. On the ‘laser’ side, HiPER’s objective is to identify the least expensive and most useful driver but not to preclude any alternative laser design that can make the facility more flexible. Before the final facility design,a major challenge for HiPER will be to enable rep-rated laser operation of around 10 Hz to demonstrate fusion in a burst mode.
HiPER is still expecting a start signal while ELI is already involved in some large DPSSL developments[13].
2. Laser design: architecture
The primary HiPER facility will be operated on a high repetition rate basis (typically 10 Hz). Again, this repetition rate is not known precisely because the repetition rate, laser efficiency and target gain are related to the cost of electricity that one would expect from the power plant design; see for example the ‘High Average Power Laser Program’[3] and the ‘Fusion cycle gain and cost of electricity’[Reference Lindl15].
This high repetition rate basis essentially means (in technological terms) that substantial new laser technology development will be required. This stems from the simple fact that the existing ‘single-shot’ technology as used by NIF or LMJ is, in general, not viable for high repetition rate requirements, although certain component technologies or techniques could readily be adapted.
Current ‘high repetition rate’ laser technology based on flashlamps could not be scaled in any feasible or credible manner to the levels of efficiency required by HiPER. DPSSL technology is very promising technologically but relatively immature in its development and certainly prohibitive in its cost at today’s prices when considering the requirements of the HiPER facility. The availability, operation and performance of large scale/aperture components and component technologies at high average power are unknown but essential entities. The level of industrial technological maturity with respect to the laser technology needs of HiPER is still some way off, even if in specific areas the industrial potential is evident. A more recent study[Reference Meier16] taking into account new gain curves predicting high gain at low (![]() $<$2 MJ) laser energy converges towards an optimum repetition rate of around 20–25 Hz.
$<$2 MJ) laser energy converges towards an optimum repetition rate of around 20–25 Hz.
Design of the laser architecture means that we are able to answer the following questions: how many beams and what is the available power per beam? The laser beam will be divided into parts or unit cells. Mechanical and electrical costs per cell scale favourably with amplifier size up to a limit that is determined by the amplifier design[Reference Le Garrec, Bourdet and Cardinali8, Reference Le Garrec, Hernandez-Gomez, Winstone and Collier17].
The latest generation of high energy lasers uses square beams with multi-pass geometries that allow higher density packaging and efficient extraction of stored energy. The laser medium is Nd-doped phosphate glass since it is available in large quantities with clear apertures of up to ![]() $40 \times 40\ {\rm cm}^{2}$. The typical bandwidth of 17 nm (FWHM) allows compression of the pulse down to 0.5 ps pulse width. NIF has operated since 2009 and LMJ is being completed and both baselines have been demonstrated on the Beamlet single laser line[Reference Henesian, Renard, Auerbach, Caird, Ehrlich, Haney, Hunt, Lawson, Manes, Milam, Sacks, Seppala, Smith, Speck, Thompson, van Wonterghem, Wegner, Weiland, Widmayer, Williams and Trenholme18] and LIL, the LMJ’s four-beam-line prototype[Reference Di-Nicola, Leidinger, Bruneau, Le Garrec, Julien, Bordenave, Maleck, Jequier, Journot, Lutz, Thiell, Féral, Graillot and Luttmann19].
$40 \times 40\ {\rm cm}^{2}$. The typical bandwidth of 17 nm (FWHM) allows compression of the pulse down to 0.5 ps pulse width. NIF has operated since 2009 and LMJ is being completed and both baselines have been demonstrated on the Beamlet single laser line[Reference Henesian, Renard, Auerbach, Caird, Ehrlich, Haney, Hunt, Lawson, Manes, Milam, Sacks, Seppala, Smith, Speck, Thompson, van Wonterghem, Wegner, Weiland, Widmayer, Williams and Trenholme18] and LIL, the LMJ’s four-beam-line prototype[Reference Di-Nicola, Leidinger, Bruneau, Le Garrec, Julien, Bordenave, Maleck, Jequier, Journot, Lutz, Thiell, Féral, Graillot and Luttmann19].
On scaling the size of the gain medium, a high gain diode-pumped solid-state amplifier will quickly suffer from amplified spontaneous emission leading to a reasonable transverse size that cannot exceed 12–15 cm[Reference Le Garrec, Bourdet and Cardinali8, Reference Le Garrec, Novaro, Tyldesley, Juarez, Sanz, Perlado, Rus, Collier and Edwards20]. This unit part or unit cell is called a single beam line (or beamlet) and one laser beam is a ‘bundle’ of ‘![]() $n$’ single beam lines.
$n$’ single beam lines.
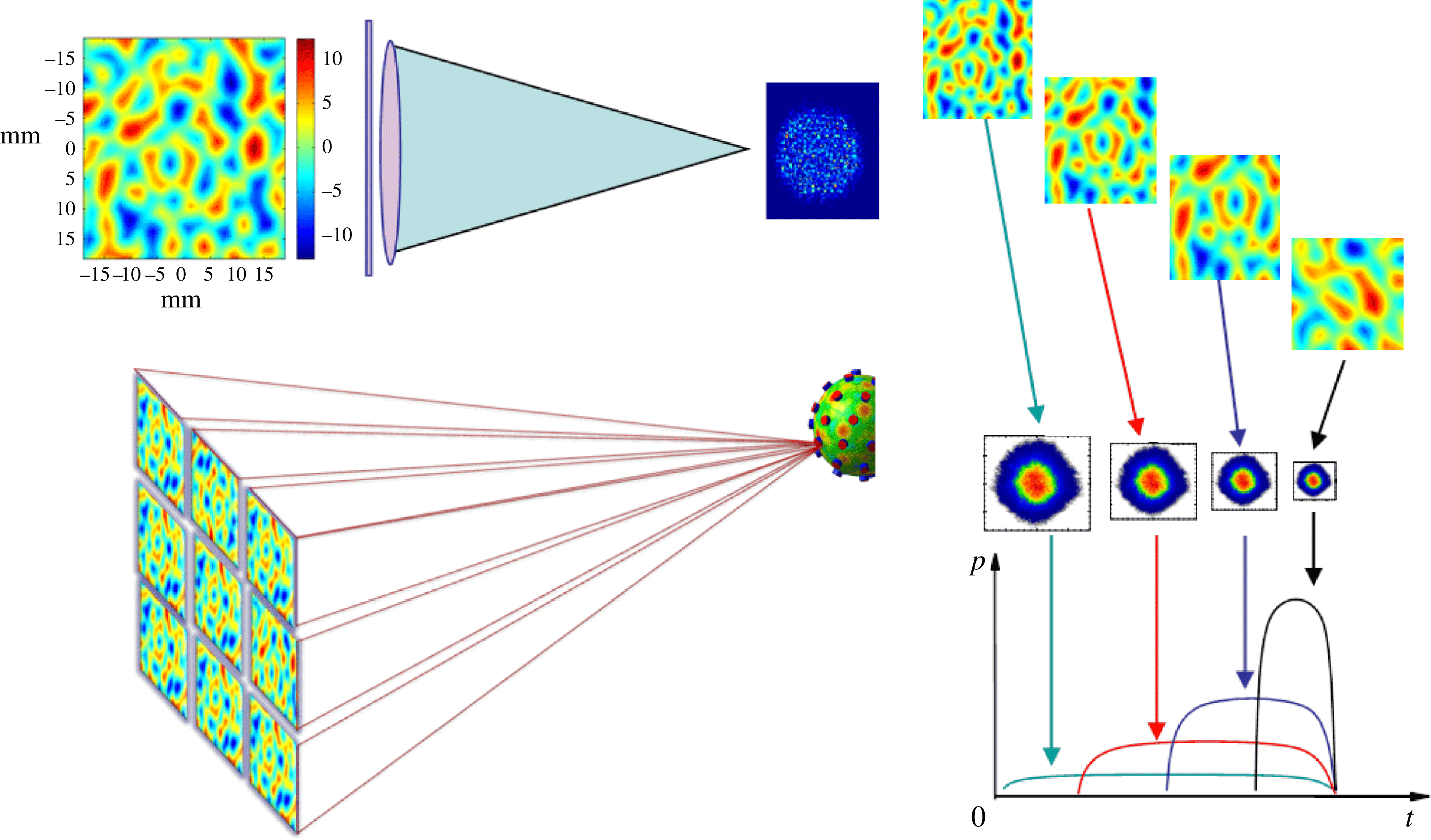
Figure 2. Top left: each beamlet has a phase plate to create a speckle pattern inside the focal spot. Bottom left: many beamlets overlap to smooth the focal spot. Right: introduction of adequate timing between beamlets leads to optical zooming; the spot size is changing during the pulse.
There is a scientific requirement for HiPER to be able to produce temporally shaped optical pulses for successful compression and ignition of the capsule. The compression beams will require a specific shape for driving this compression. The current technology allows pulses to be shaped in time by using optical modulators in conjunction (also called an arbitrary wveform generator, AWG). The temporal resolution is limited by the AWG. A schematic of a typical laser pulse used for compression beams for fast ignition and shock ignition is shown in Figure 1. Both solutions are still under consideration asdiscussed in a recent issue of Nuclear Fusion[Reference Tabak, Norreys, Tikhonchuk and Tanaka21]. In both cases, the compression pulse is preceded by an adiabatic shaping picket (of 100–200 ps duration) from Ref. [Reference Le Garrec, Atzeni, Batani, Gizzi, Ribeyre, Schurtz, Schiavi, Ertel, Collier, Edwards, Perlado, Honrubia and Rus22]. The times of the initial shocks are in the nanosecond regime whilst the final rise of the pulse can be ![]() $\sim $100 ps.
$\sim $100 ps.
When there are multiple beams, it is possible to shape the pulse by adding different pulse shapes. A bundle of beamlets can be seeded from the same front-end. The pulse injected into each bundle to be amplified can be designed to have a pulse shape with several shocks and the shock levels and times can then be adjusted at the front-end by the AWG which provides the different voltages to the optical modulators. The pulse should be designed to carefully send a series of shocks to the capsule with the correct timings to achieve ignition. Some of the crucial parameters of the pulse shape are the power of the first step and the timing of the different steps.
Moreover, our bundle principle allows the building of different complex pulse shapes and different overlapping focal spots because it is based on time-delayed pulse shapes associated with different beamlets and then leading to optical zooming[Reference Canaud and Garaude23, Reference Temporal, Canaud and Le Garrec24] on reducing the focal spot step by step during the pulse (Figure 2). Included in the design as a mandatory requirement is the use of a phase plate to both condition the focal spot and create the necessary stationary speckle pattern. This bundle design has many advantages when considering focal spot conditioning, optical zooming, and pulse shaping; it has been described in detail in[Reference Le Garrec, Atzeni, Batani, Gizzi, Ribeyre, Schurtz, Schiavi, Ertel, Collier, Edwards, Perlado, Honrubia and Rus22–Reference Temporal, Canaud and Le Garrec24]. Both NIF and LMJ have shown that in solid-state lasers, the bandwidth is large enough to withstand phase modulation as a necessary requirement for beam smoothing and stimulated Brilloouin scattering (SBS) suppression. SBS is much less demanding than beam smoothing and the bandwidth is large enough for SBS suppression. This is true for Nd:glass where the emission bandwidth is large enough, but it is a limiting factor in Yb:YAG when saturation occurs. For accessing larger bandwidths, ![]() ${\rm Yb\! :\! CaF}_{2}$ is even better than glass.
${\rm Yb\! :\! CaF}_{2}$ is even better than glass.
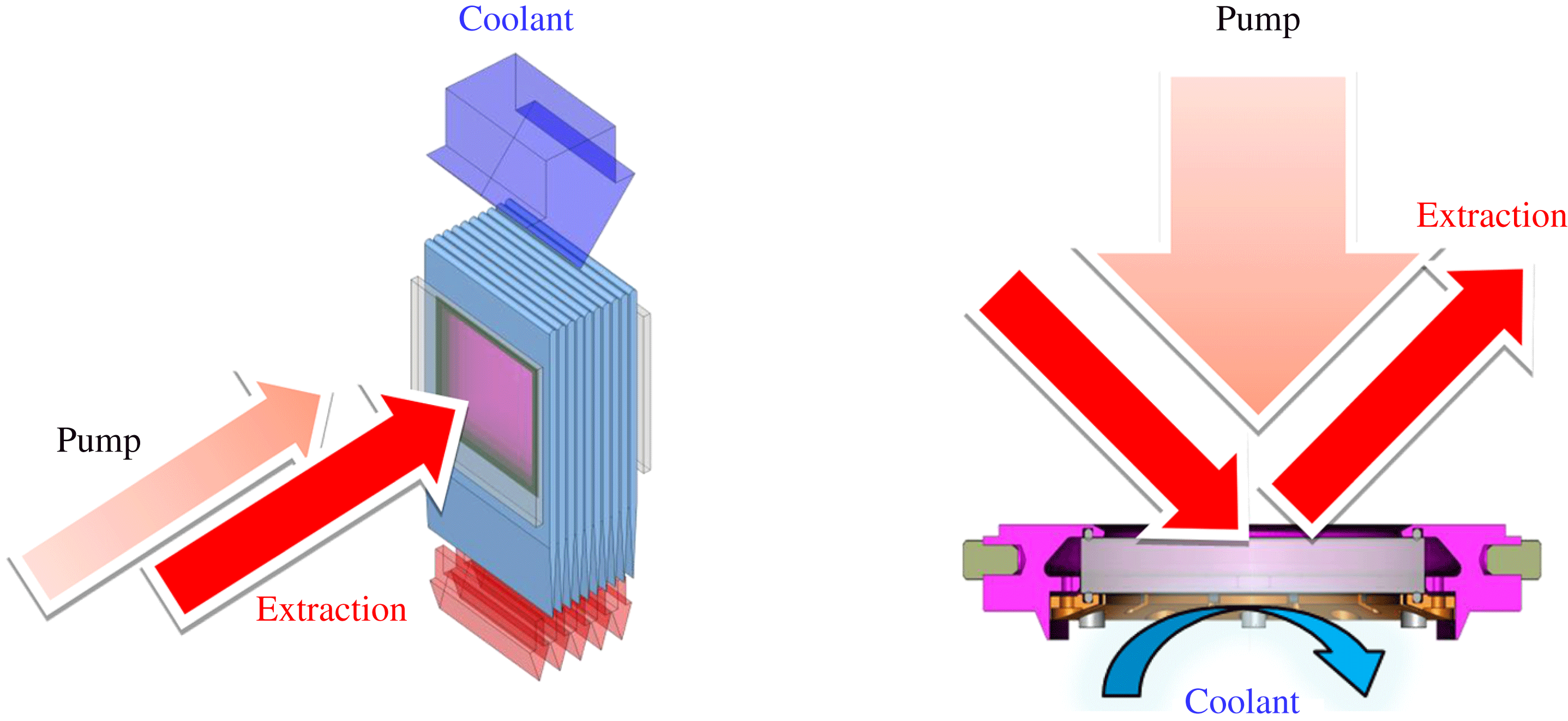
Figure 3. Design of two diode-pumped amplifiers from Ref. [Reference Chanteloup, Albach, Lucianetti, Ertel, Banerjee, Mason, Hernandez-Gomez, Collier, Hein, Wolf, Körner and Le Garrec25]. The left is Mercury-like[Reference Bayramian26] and/or Dipole-like[Reference Banerjee, Ertel, Mason, Phillips, Siebold, Lœser, Hernandez-Gomez and Collier27] and the right is Lucia-like[28].
3. Laser architecture and thermal management of the laser medium
If high average power is achieved, it means that the laser medium is able to sustain a very high thermal load. For most high output power applications, several unique advantages have made Yb the dopant of choice. A comparison between Yb- and Nd-doped lasers shows that there is a real advantage with Yb because the quantum defect is less than 9%, almost 3 times lower than Nd. This can be even better when pumping the ‘zero line’[Reference Le Garrec, Bourdet and Cardinali8].
For a kJ-level amplifier at 10 Hz repetition rate, the average power will be 10 kW. Assuming a typical ![]() $15{\%}\pm 5{\%}$ pump-to-laser efficiency, a 1 kJ amplifier will require from 5 to 10 kJ pump energy. This gives 10,000 to 20,000 diode bars (assuming that 1 bar is 500 W peak power at 1 ms pulse duration) per kJ amplifier. If the pump time is 1 ms, a 10 Hz repetition rate will require a 1% duty cycle of the diode bars. In order to perform this task, four approaches were explored during the HiPER programme. Two were related to using Yb:YAG gain medium, one was with Yb-doped calcium fluoride and the last one looked at Yb-doped glass fibers[Reference Chanteloup, Albach, Lucianetti, Ertel, Banerjee, Mason, Hernandez-Gomez, Collier, Hein, Wolf, Körner and Le Garrec25]. Although no down-selection process has been possible during the HiPER preparatory phase, it is proposed that the main amplifier will be made of a set of at least two amplifiers in a multiple-pass configuration (as used in LMJ or NIF) to reach 1 kJ in a single beam with 12–15 cm diameter. At that point, it becomes obvious that Yb-doped calcium fluoride is more suitable for short pulse generation in a non-saturated amplifier as the saturation fluence is far too high (
$15{\%}\pm 5{\%}$ pump-to-laser efficiency, a 1 kJ amplifier will require from 5 to 10 kJ pump energy. This gives 10,000 to 20,000 diode bars (assuming that 1 bar is 500 W peak power at 1 ms pulse duration) per kJ amplifier. If the pump time is 1 ms, a 10 Hz repetition rate will require a 1% duty cycle of the diode bars. In order to perform this task, four approaches were explored during the HiPER programme. Two were related to using Yb:YAG gain medium, one was with Yb-doped calcium fluoride and the last one looked at Yb-doped glass fibers[Reference Chanteloup, Albach, Lucianetti, Ertel, Banerjee, Mason, Hernandez-Gomez, Collier, Hein, Wolf, Körner and Le Garrec25]. Although no down-selection process has been possible during the HiPER preparatory phase, it is proposed that the main amplifier will be made of a set of at least two amplifiers in a multiple-pass configuration (as used in LMJ or NIF) to reach 1 kJ in a single beam with 12–15 cm diameter. At that point, it becomes obvious that Yb-doped calcium fluoride is more suitable for short pulse generation in a non-saturated amplifier as the saturation fluence is far too high (![]() $25\ {\rm J\ cm}^{-2}$ at room temperature), because the maximum fluence at the amplifier output must be lower than the laser damage fluence of the weakest optical component of the amplifier. As an example, let us consider
$25\ {\rm J\ cm}^{-2}$ at room temperature), because the maximum fluence at the amplifier output must be lower than the laser damage fluence of the weakest optical component of the amplifier. As an example, let us consider ![]() $10\ {\rm J\ cm}^{-2}$ damage fluence (which is quite easily accessible at
$10\ {\rm J\ cm}^{-2}$ damage fluence (which is quite easily accessible at ![]() $1\ \mu {\rm m}$ wavelength but would not be possible at the third harmonic) and a beam whose near-field modulation depth equals 1.5; this means that the average fluence in the beam should not exceed
$1\ \mu {\rm m}$ wavelength but would not be possible at the third harmonic) and a beam whose near-field modulation depth equals 1.5; this means that the average fluence in the beam should not exceed ![]() $6.7\ {\rm J\ cm}^{-2}$ and that 1 kJ energy can be extracted for a
$6.7\ {\rm J\ cm}^{-2}$ and that 1 kJ energy can be extracted for a ![]() $150\ {\rm cm}^{2}$ aperture.
$150\ {\rm cm}^{2}$ aperture.
One of the possible solutions for thermal management of the gain medium is for the gain medium to be split into many thin slabs, allowing efficient cooling through a gas cooling technique like the one that has been tested during the Mercury Program[Reference Bayramian26]. Moreover, amplifiers can be run at low temperature in order to increase both the laser efficiency and the thermal conductivity of the laser medium[Reference Brown6, Reference Le Garrec, Bourdet and Cardinali8]. Merging both leads to even better results like in the Dipole Programme[Reference Banerjee, Ertel, Mason, Phillips, Siebold, Lœser, Hernandez-Gomez and Collier27]. Another solution that is still being studied for the Lucia Program[28] is the well-known ‘mirror’ configuration that is close to the thin-disc design (Figure 3)[Reference Stewen, Contag, Larionov, Giesen and Hugel29].
4. Diode-pumped solid-state lasers (DPSSLs)
Some researchers still favour KrF laser technology[Reference Bodner, Schmitt and Sethian2], mainly because this type of laser can operate at UV wavelength while most DPSSLs operate at around ![]() $1\ \mu {\rm m}$ and therefore need frequency conversion. Almost everything has been said about DPSSLs, the different ways of pumping[Reference Grechin and Nikolaev30] and the level of performance[Reference Bowman31]. This also includes cryogenic cooling[Reference Rand, Cheng and Woolf32] and the development of ceramic materials[Reference Sanghera, Kim, Villalobos, Shaw, Baker, Frantz, Sadowski and Aggarwal33]. Cryogenic cooling is not new (the second solid-state laser ever demonstrated was cryogenically cooled uranium-doped calcium fluoride[Reference Sorokin and Stevenson34]) and it was re-introduced roughly 15 years ago[Reference Brown6, Reference Numazawa, Arai, Hu and Noda35]. CW and rep-rated laser are close to the multi-kW level[Reference Rand, Cheng and Woolf32] and some huge laser systems for military purposes have already reached 100 kW[36], as reported in Ref. [Reference Sanghera, Kim, Villalobos, Shaw, Baker, Frantz, Sadowski and Aggarwal33].
$1\ \mu {\rm m}$ and therefore need frequency conversion. Almost everything has been said about DPSSLs, the different ways of pumping[Reference Grechin and Nikolaev30] and the level of performance[Reference Bowman31]. This also includes cryogenic cooling[Reference Rand, Cheng and Woolf32] and the development of ceramic materials[Reference Sanghera, Kim, Villalobos, Shaw, Baker, Frantz, Sadowski and Aggarwal33]. Cryogenic cooling is not new (the second solid-state laser ever demonstrated was cryogenically cooled uranium-doped calcium fluoride[Reference Sorokin and Stevenson34]) and it was re-introduced roughly 15 years ago[Reference Brown6, Reference Numazawa, Arai, Hu and Noda35]. CW and rep-rated laser are close to the multi-kW level[Reference Rand, Cheng and Woolf32] and some huge laser systems for military purposes have already reached 100 kW[36], as reported in Ref. [Reference Sanghera, Kim, Villalobos, Shaw, Baker, Frantz, Sadowski and Aggarwal33].
The Solid-State Heat Capacity Laser was the first DPSSL to provide 67 kW in 2006 using five ceramic 10 cm aperture Nd:YAG slabs[Reference Yamamoto, Parker, Allen, Allmon, Alviso, Barty, Bhachu, Boley, Burnham, Combs, Cutter, Fochs, Gonzales, Hurd, LaFortune, Manning, McClelland, Merrill, Molina, Parks, Pax, Posey, Rotter, Roy, Rubenchik, Soules and Webb37]. This average output power was obtained in a ![]() $1/2$ second burst mode, 500 ms pulse width, at 200 Hz rep-rate. Neither the efficiency nor the beam quality were known at 67 kW. Then, in 2009 Northrop Grumman Corp. (NGC) demonstrated 100 kW output power[36]; this company utilizes ‘laser amplifier chains’, each producing approximately 15 kW of power in a high quality beam. Seven laser chains were combined to produce a single beam of 105.5 kW. The seven-chain laser demonstrator ran for more than 5 min and achieved an electro-optical efficiency of 19.3%, reaching full power in less than 0.6 s, all with a beam quality of better than 3.0 (from the Joint High Power Solid-State Laser (JHPSSL) Program[36]).
$1/2$ second burst mode, 500 ms pulse width, at 200 Hz rep-rate. Neither the efficiency nor the beam quality were known at 67 kW. Then, in 2009 Northrop Grumman Corp. (NGC) demonstrated 100 kW output power[36]; this company utilizes ‘laser amplifier chains’, each producing approximately 15 kW of power in a high quality beam. Seven laser chains were combined to produce a single beam of 105.5 kW. The seven-chain laser demonstrator ran for more than 5 min and achieved an electro-optical efficiency of 19.3%, reaching full power in less than 0.6 s, all with a beam quality of better than 3.0 (from the Joint High Power Solid-State Laser (JHPSSL) Program[36]).
Textron reported almost the same performance in 2010 with six modules each of over 16 kW[Reference Mandl and Klimek38]. Some data are available on the beam quality for the three-module experiments: between 2.4 ![]() $\times $ DL at 15 kW and 3.3
$\times $ DL at 15 kW and 3.3 ![]() $\times $ DL at 30 kW (
$\times $ DL at 30 kW (![]() $\times $ DL
$\times $ DL ![]() $=$ times diffraction limit).
$=$ times diffraction limit).
As already pointed out in Ref. [Reference Le Garrec39], there are very efficient DPSSLs, but when looking at the beam quality (or ![]() ${\rm M}^{2}$), only a few systems can be considered as really efficient. The only highly efficient systems with highest beam quality (i.e.,
${\rm M}^{2}$), only a few systems can be considered as really efficient. The only highly efficient systems with highest beam quality (i.e., ![]() ${\rm M}^{2}$ close to 1) are CW lasers at cryogenic temperature[Reference Brasseur, Abeeluck, Awtry, Meng, Shortoff, Miller, Hampton, Cuchiara and Newmann40–Reference Furuse, Kawanaka, Saiki, Imasaki, Fujita, Ishii, Takeshita and Miyanaga42].
${\rm M}^{2}$ close to 1) are CW lasers at cryogenic temperature[Reference Brasseur, Abeeluck, Awtry, Meng, Shortoff, Miller, Hampton, Cuchiara and Newmann40–Reference Furuse, Kawanaka, Saiki, Imasaki, Fujita, Ishii, Takeshita and Miyanaga42].
Apart from multi-kW-level lasers for military applications, Mercury has had the best results: 55 J at 10 Hz rep-rate at 1047 nm for 8.5 h (peak at 62 J)[Reference Bayramian26, Reference Le Garrec39].
This is because Quasi-CW (QCW) diode bars have a typical 1% duty cycle which makes them suitable for pumping Yb at 10 Hz (excited-state lifetime is typically 1 ms in garnet). The use of CW diodes means either CW operation or a few kHz repetition rate (this is true for both Nd- and Yb-doped solid-state hosts).
There are several programmes involving diode-pumped Yb lasers at the kW level[12], but none of them are able to reach the expected kW level (100 J at 10 Hz). Mercury[Reference Bayramian26] has had the best results: 55 J at 10 Hz rep-rate at 1047 nm for 8.5 h (peak at 62 J); 32 J at 10 Hz rep-rate at 523 nm in YCOB with a 5.5 cm aperture. At 1047 nm, the enclosed energy at 80% is four times diffraction limited.
The DPSSL programmes decided to organize a seminar as early as 2003, gathering Mercury[43], Polaris[Reference Hornung, Keppler, Bödefeld, Kessler, Liebetrau, Körner, Hellwing, Schorcht, Jäckel, Sävert, Polz, Arunachalam, Hein and Kaluza44], Halna[Reference Kawashima, Kanabe, Matsumoto, Yasuhara, Sekine, Kurita, Yamanaka, Furukawa, Miyamoto, Kanzaki, Kan, Miyanaga, Nakatsuka, Izawa, Nakai and Yamanaka45], Lucia[28], and Dipole[Reference Banerjee, Ertel, Mason, Phillips, Siebold, Lœser, Hernandez-Gomez and Collier27, 46]. European programmes are supported by Laserlab[47] and are linked to ELI[13] and HiPER[14]. Nevertheless, and although there are engineering solutions to improve the thermal management of the gain medium[Reference Arzakantsyan, Ananyan, Gevorgyan and Chanteloup48] and the efficiency of the cooling, the maximum output energy record is still the one achieved by Mercury[Reference Bayramian26]. The current trend for improving efficiency is to be able to combine several advantages while introducing engineering solutions: cryogenic cooling must be addressed to increase the overall efficiency, keeping in mind the efficiency of the cooling cycle. A factor of 3 has been shown to be possible[Reference Le Garrec, Bourdet and Cardinali8]. Increase of the stored energy is also part of the solution because large gain media are becoming available thanks to ceramic developments. Nevertheless, when dealing with apertures of around 20 cm, well-known classical glass material can provide excellent results when it is associated with new amplifier designs, as has been published recently with Nd-doped phosphate glass[Reference Caird, Agrawal, Bayramian, Beach, Britten, Chen, Cross, Ebbers, Erlandson, Feit, Freitas, Ghosh, Haefner, Homœlle, Ladran and Latkowski49, Reference Erlandson, Aceves, Bayramian, Bullington, Beach, Boley, Caird, Deri, Dunne, Flowers, Henesian, Manes, Moses, Rana, Schaffers, Spaeth, Stolz and Telford50]. At this stage, the best solution for demonstrating that it is possible to combine these efforts is to build a prototype.
Some may argue that the expected DPSSL efficiency is lower than expected and is not suitable for a power plant design. As pointed out in Ref. [Reference Le Garrec39], DPSSLs near the kW level have a moderate efficiency (![]() $\ll $10%), or when they are over 10% efficiency, then the beam quality is low (
$\ll $10%), or when they are over 10% efficiency, then the beam quality is low (![]() ${\rm M}^{2}{>}10$) and not suitable for either propagation or frequency conversion. According to the fusion cycle gain model[Reference Lindl15], one can choose a set of parameters such that the high thermonuclear gain can compensate for low driver efficiency: the lower the driver efficiency, the higher the thermonuclear gain. For commercial viability, the laser efficiency should be close to 7%, although some recent work claims that higher values (15%) should be accessible[Reference Erlandson, Aceves, Bayramian, Bullington, Beach, Boley, Caird, Deri, Dunne, Flowers, Henesian, Manes, Moses, Rana, Schaffers, Spaeth, Stolz and Telford50].
${\rm M}^{2}{>}10$) and not suitable for either propagation or frequency conversion. According to the fusion cycle gain model[Reference Lindl15], one can choose a set of parameters such that the high thermonuclear gain can compensate for low driver efficiency: the lower the driver efficiency, the higher the thermonuclear gain. For commercial viability, the laser efficiency should be close to 7%, although some recent work claims that higher values (15%) should be accessible[Reference Erlandson, Aceves, Bayramian, Bullington, Beach, Boley, Caird, Deri, Dunne, Flowers, Henesian, Manes, Moses, Rana, Schaffers, Spaeth, Stolz and Telford50].
The last critical parameter for DPSSLs is the cost of laser diodes because only quasi-continuous mode operation (QCW) at low duty cycle (1%) is possible for this type of medium repetition rate (10–20 Hz). This excludes the possibility of using CW diodes for which the market is larger. Some early studies[Reference Orth, Payne and Krupke51] were confident that the cost will decrease quickly to a few cents per peak watt. The cost of QCW laser diodes is decreasing but we have not yet been able to reach the expected level for two reasons: first, because the market of QCW laser diodes is restricted to a small market of scientific and military lasers and, second, because the cost of packaging laser diode arrays as stacks is still much greater than the cost of the semiconductor itself. It will be possible to access mass production for stacked QCW diode arrays at low cost if the market becomes large enough that laser diode manufacturers move from manual processing to automated manufacture.
5. All-fiber architecture
A new amplifying concept designed to produce high energy in either short or long pulses using coherent or incoherent addition of a few millions of fibers was proposed in 2007 at the IFSA conference[Reference Mourou, Labaune, Hulin and Galvanauskas52].
Yb-doped fibers offer high output powers tunable over a broad range of wavelengths, from around 975 to 1200 nm. Yb also has a relatively small quantum defect: because the pump wavelength (typically 915–975 nm) is close to the lasing wavelength, very little energy is lost to heating. Furthermore, unlike other lanthanide ions, Yb has only one excited state, is not subject to complications arising from excited-state absorption (ESA), and is relatively immune to self-quenching processes. Consequently, designers can incorporate high concentrations of Yb ions while maintaining excellent conversion efficiencies (typically greater than 75%). For this reason, the industry has focused on the development of Yb-doped fibers.
Whatever the fiber design is, it must not limit the total achievable output power and in pulsed laser devices the average power, peak power and pulse energy.
One of the major advances in fiber technology in recent years has been the advent of large-mode-area (LMA) fibers, and the potential for these fibers to deliver diffraction-limited beam quality with mode-field areas greater than 10 times that for standard telecom type fibers. A single-fiber laser can deliver an output power of over 1 kW, and 10 kW in CW mode is available. Beam combining has shown that 4 kW is possible with an almost diffraction-limited beam[Reference Yu, Augst, Redmond, Goldizen, Murphy, Sanchez and Fan53].
Scaling is possible because fibers have even more advantages than bulk solid-state lasers[Reference Dawson, Messerly, Beach, Shverdin, Stappaerts, Sridharan, Pax, Heebner, Siders and Barty54, Reference Smith, Do, Hadley and Farrow55], but one has to be careful because in pulse mode:
∙ the repetition rate must be quite high (
 $\gg $1 kHz and more likely 10–100 kHz) to deplete the gain;
$\gg $1 kHz and more likely 10–100 kHz) to deplete the gain;∙ the energy per pulse is in the mJ range.
There are engineering solutions to decrease the repetition rate and increase the pulse energy, like cavity stacking and cavity dumping, but this is only possible at high repetition rate (time delay line) and moderate cavity finesse[Reference Potoma, Evans, Xie, Jones and Ye56, Reference Vidne, Rosenbluh and Hansch57]. Therefore, the application should use the best that the technology can provide[Reference Mourou, Brocklesby, Tajima and Limpert58].
Nevertheless, the best results are at the 10 kW level: beam combining at 8.2 kW with ![]() ${\rm M}^{2} = 4.3$[Reference Wirth, Schmidt, Tsybin, Schreiber, Eberhardt, Limpert, Tünnermann, Ludewigt, Gowin, Have and Jung59] and 10 kW from commercially available multimode fiber[60].
${\rm M}^{2} = 4.3$[Reference Wirth, Schmidt, Tsybin, Schreiber, Eberhardt, Limpert, Tünnermann, Ludewigt, Gowin, Have and Jung59] and 10 kW from commercially available multimode fiber[60].
These major high average power achievements are shown in Figure 4.
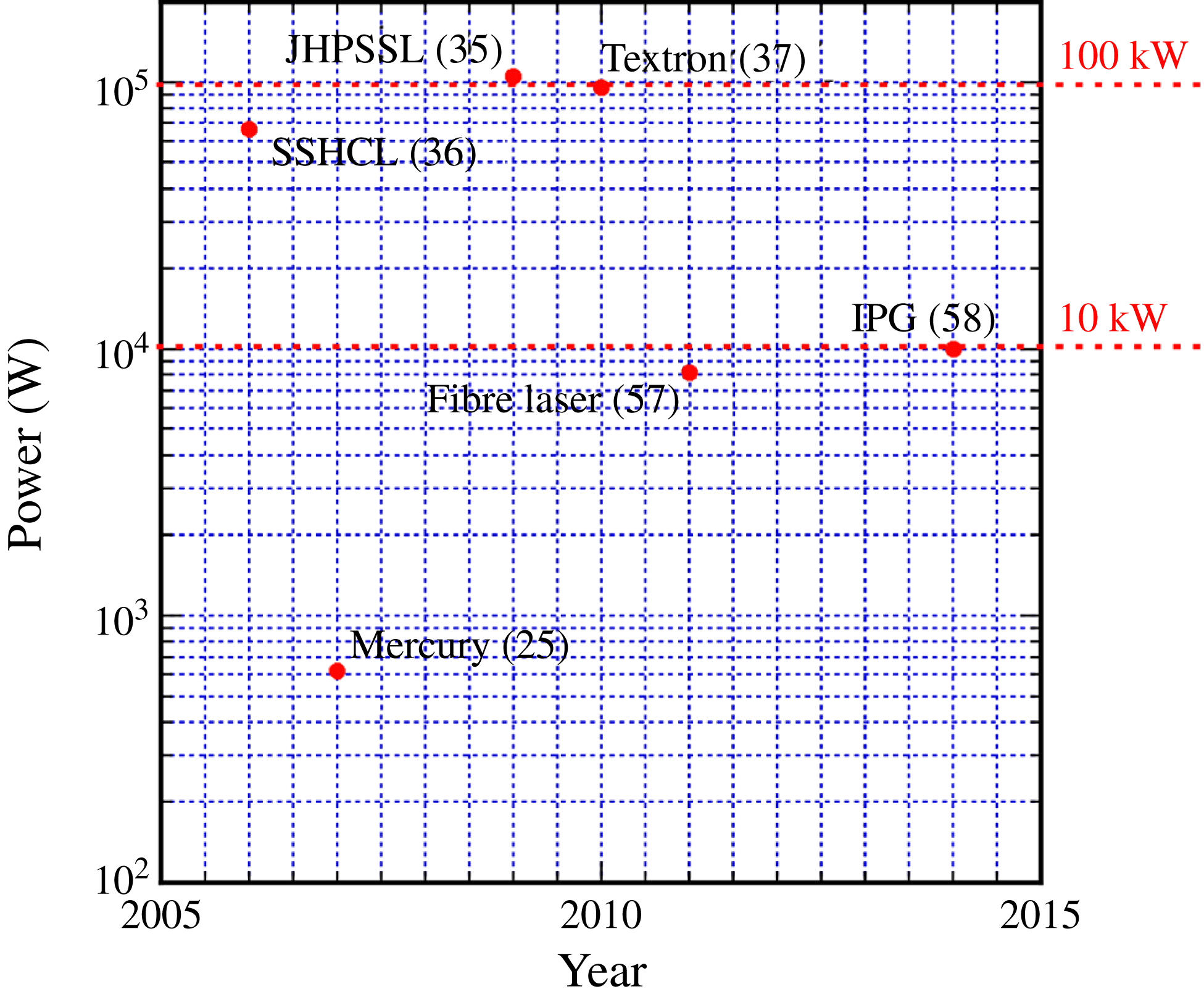
Figure 4. Evolution of laser output power versus year for some DPSSLs: Mercury[Reference Bayramian26], SSHCL[Reference Yamamoto, Parker, Allen, Allmon, Alviso, Barty, Bhachu, Boley, Burnham, Combs, Cutter, Fochs, Gonzales, Hurd, LaFortune, Manning, McClelland, Merrill, Molina, Parks, Pax, Posey, Rotter, Roy, Rubenchik, Soules and Webb37], Textron[Reference Mandl and Klimek38], JHPSSL[36] and also four combined fiber lasers[Reference Wirth, Schmidt, Tsybin, Schreiber, Eberhardt, Limpert, Tünnermann, Ludewigt, Gowin, Have and Jung59]. Also shown is one commercially available multimode fiber laser system[60].
6. Conclusion
DPSSLs may have the potential efficiency and repetition rate required for power production. The architecture design shows that the 1 kJ range is accessible per beam unit cell, leading to 10 kW average power, which is compliant with the best ever achieved results for military purposes.
Thermal management is an engineering problem to be solved and many improvements have been made in solid-state lasers by using Yb instead of Nd, considering cryogenic cooling and the use of ceramic gain media instead of single crystals. Nevertheless, there is a full list of engineering solutions to be implemented: pulse shaping, beam shaping, beam smoothing, adaptive optics and even large single crystals which are becoming available with free apertures of over 100 mm.
Beam combining is progressing very quickly when pushed by specific applications: one example is the fast development of diode-pumped alkali lasers for airborne applications[Reference Krupke61, Reference Gao, Chen, Xie, Li, Zhang, Yang, Guo and Guo62].
Moreover, flashlamp-pumped solid-state lasers are still in the race when dealing with kJ-range outputs at moderate repetition rates[Reference Ditmire63] for pumping Ti:sapphire amplifier[28] and for developing mixed-glass technology[Reference Ditmire63, Reference Gaul, Martinez, Blakeney, Jochmann, Ringuette, Hammond, Borger, Escamilla, Douglas, Henderson, Dyer, Erlandson, Cross, Caird, Ebbers and Ditmire64] for 10 PW lasers.
Acknowledgements
The author gratefully acknowledges the support of the Funding Agencies in undertaking this work (EC FP7 project number 211737): EC, European Commission, MŠMT, Ministry of Education, Youth and Sports of the Czech Republic, and STFC, Science and Technology Facility Council of the United Kingdom.





