1 Introduction
In the recent years, a diode-pumped alkali laser (DPAL) has been extensively studied due to the potential for its excellent physical features[Reference Wang, Kasamatsu, Zheng, Miyajima, Fukuoka, Matsuoka, Niigaki, Kubomura, Hiruma and Kan1–Reference Zhdanov and Knize3]. The oscillator of a DPAL usually contains an enclosed glass cell, in which the vapor of neutral alkali (K, Rb, Cs) and several kinds of buffer gases (helium and hydrocarbon with small molecular weight) are sealed with a certain pressure[Reference Krupke, Beach, Kanz and Payne4–Reference Zhang, Wang, Cai, Xue, Han, Wang and Liao6]. In 2006, Payne et al. proposed a patent describing a new kind of DPAL in which a hollow-core photonic-crystal fiber (HC-PCF) is used as the vapor container[Reference Payne, Beach, Dawson and Krupke7]. Unlike a normal DPAL, such an integrated design is thought to have higher stability. And the optical coupling efficiency of this system can be improved significantly comparing with the traditional configuration. Slepkov et al. also demonstrated the possibility of introducing alkali vapor into a standard hollow-core fiber with sufficient gas density[Reference Slepkov, Bhagwat, Venkataraman, Londero and Gaeta8]. Recently, Sintov et al. calculated the physical features of a rubidium vapor-based fiber laser using a simple mathematical model, in which the HC-PCF-DPAL was treated as a three-level laser system[Reference Sintov, Malka and Zalevsky9].
Generally, alkalis are the most easily ionized atomic species, especially for rubidium and cesium. Figure 1 illustrates the energy level diagram for Cs atoms. The electrons in cesium atoms are pumped from the
![]() $6^{2}S_{1/2}$
level to the
$6^{2}S_{1/2}$
level to the
![]() $6^{2}P_{3/2}$
level corresponding to the
$6^{2}P_{3/2}$
level corresponding to the
![]() $D_{2}$
line (852.3 nm). After a rapid relaxation in the fine structure with the aid of some alkanes with small hydrocarbon molecules, electrons fall back to the ground state with stimulated emission corresponding to the
$D_{2}$
line (852.3 nm). After a rapid relaxation in the fine structure with the aid of some alkanes with small hydrocarbon molecules, electrons fall back to the ground state with stimulated emission corresponding to the
![]() $D_{1}$
line (894.6 nm). Under the condition of high-powered pump, the electrons will be excited to the higher levels (
$D_{1}$
line (894.6 nm). Under the condition of high-powered pump, the electrons will be excited to the higher levels (
![]() $6^{2}D_{5/2,3/2}$
and
$6^{2}D_{5/2,3/2}$
and
![]() $8^{2}S_{1/2}$
) by energy pooling collisions. Further, ionization processes including photo-ionization and Penning ionization will occur on the
$8^{2}S_{1/2}$
) by energy pooling collisions. Further, ionization processes including photo-ionization and Penning ionization will occur on the
![]() $6^{2}D_{5/2,3/2}$
and
$6^{2}D_{5/2,3/2}$
and
![]() $8^{2}S_{1/2}$
levels resulting in decrease of the density of neutral atoms.
$8^{2}S_{1/2}$
levels resulting in decrease of the density of neutral atoms.

Figure 1. Energy level diagram for a cesium atom.
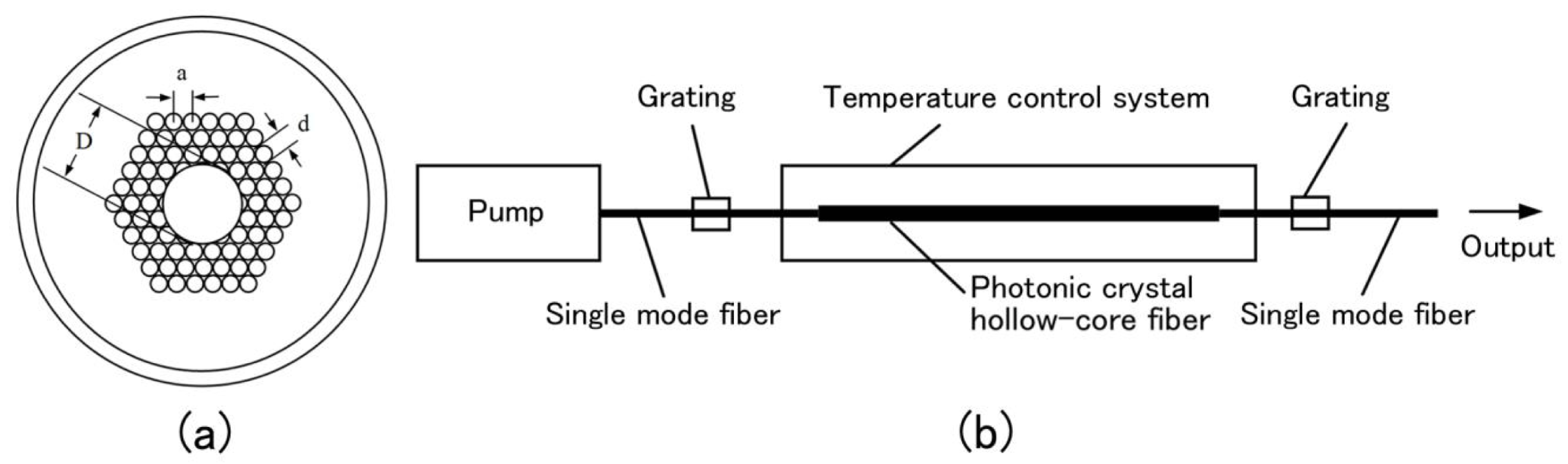
Figure 2. (a) Transverse view of an HC-PCF and (b) the schematic diagram of the diode-pumped cesium vapor HC-PCF laser system.
To deeply study the kinetics of an HC-PCF-DPAL, we construct a quasi-five-level model with the cesium vapor as a gain medium in this report. The deleterious processes of energy pooling and ionization are taken into account in the theoretical model. The absorbed power, output power, and optical-to-optical efficiency versus the pump power have been evaluated. In addition, the influences of energy pooling, Penning ionization and Photo-ionization on the output features of a DPAL are also evaluated. To the best of our knowledge, there have not been any similar reports about a diode-pumped cesium vapor HC-PCF laser.
2 Theoretical analyses
Figure 2(a) shows the transverse view of an HC-PCF, which consists of a center hollow core with the diameter
![]() $D$
and several rings circular hole (honeycomb lattice) with the diameter
$D$
and several rings circular hole (honeycomb lattice) with the diameter
![]() $d$
and the hole-to-hole spacing
$d$
and the hole-to-hole spacing
![]() $a$
. By properly choosing the geometric parameter values, a wide bandgap guiding can be realized[Reference Wang, Wheeler, Couny, Roberts and Benabid10]. The schematic diagram of this laser system is shown in Figure 2(b). Cesium vapor and buffer gases are introduced into the center hole of an HC-PCF, which is connected with two single mode fibers (SMFs).
$a$
. By properly choosing the geometric parameter values, a wide bandgap guiding can be realized[Reference Wang, Wheeler, Couny, Roberts and Benabid10]. The schematic diagram of this laser system is shown in Figure 2(b). Cesium vapor and buffer gases are introduced into the center hole of an HC-PCF, which is connected with two single mode fibers (SMFs).
By taking the processes of energy pooling, photo-ionization, Penning ionization, and recombination into account, the three-level rate equations used in our previous simulation are extended to quasi-five-level rate equations. We designate the number densities of the
![]() $6^{2}S_{1/2}$
,
$6^{2}S_{1/2}$
,
![]() $6^{2}P_{1/2}$
,
$6^{2}P_{1/2}$
,
![]() $6^{2}P_{3/2}$
,
$6^{2}P_{3/2}$
,
![]() $6^{2}D_{5/2,3/2}$
and
$6^{2}D_{5/2,3/2}$
and
![]() $8^{2}S_{1/2}$
, and ionized levels to be
$8^{2}S_{1/2}$
, and ionized levels to be
![]() $n_{1}$
,
$n_{1}$
,
![]() $n_{2}$
,
$n_{2}$
,
![]() $n_{3}$
,
$n_{3}$
,
![]() $n_{4}$
and
$n_{4}$
and
![]() $n_{5}$
, respectively. Therefore, the total number density
$n_{5}$
, respectively. Therefore, the total number density
![]() $n_{0}$
can be expressed as
$n_{0}$
can be expressed as
![]() $n_{0}=n_{1}+n_{2}+n_{3}+$
$n_{0}=n_{1}+n_{2}+n_{3}+$
![]() $n_{4}+n_{5}$
. The appropriate rate equations can be expressed as follows[Reference An, Wang, Han, Cai, Zhou, Zhang, Xue, Wang, Gao and Jiang11]:
$n_{4}+n_{5}$
. The appropriate rate equations can be expressed as follows[Reference An, Wang, Han, Cai, Zhou, Zhang, Xue, Wang, Gao and Jiang11]:
 $$\begin{eqnarray}\displaystyle \frac{\text{d}n_{1}}{\text{d}t} & = & \displaystyle -\unicode[STIX]{x1D6E4}_{P}+\unicode[STIX]{x1D6E4}_{L}+\frac{n_{2}}{\unicode[STIX]{x1D70F}_{D_{1}}}+\frac{n_{3}}{\unicode[STIX]{x1D70F}_{D_{2}}}+\frac{n_{4}}{\unicode[STIX]{x1D70F}_{4}}\nonumber\\ \displaystyle & & \displaystyle +\,k_{EP2}(n_{2})^{2}+k_{EP3}(n_{3})^{2}\nonumber\\ \displaystyle & & \displaystyle +\,k_{PI}n_{4}(n_{2}+n_{3}),\nonumber\\ \displaystyle \frac{\text{d}n_{2}}{\text{d}t} & = & \displaystyle -\unicode[STIX]{x1D6E4}_{L}+\unicode[STIX]{x1D6FE}_{32}(T_{w})\left\{\vphantom{\left[2\exp \left(-\frac{\unicode[STIX]{x1D6E5}E}{k_{B}T_{w}}\right)-1\right]}[n_{3}-n_{2}]\right.\nonumber\\ \displaystyle & & \displaystyle \left.-\,\left[2\exp \left(-\frac{\unicode[STIX]{x1D6E5}E}{k_{B}T_{w}}\right)-1\right]n_{2}\right\}-\frac{n_{2}}{\unicode[STIX]{x1D70F}_{D_{1}}}\nonumber\\ \displaystyle & & \displaystyle -\,2k_{EP2}(n_{2})^{2}-k_{PI}n_{2}n_{4},\nonumber\\ \displaystyle \frac{\text{d}n_{3}}{\text{d}t} & = & \displaystyle \unicode[STIX]{x1D6E4}_{P}-\unicode[STIX]{x1D6FE}_{32}(T_{w})\left\{\vphantom{\left[2\exp \left(-\frac{\unicode[STIX]{x1D6E5}E}{k_{B}T_{w}}\right)-1\right]}[n_{3}-n_{2}]\right.\nonumber\\ \displaystyle & & \displaystyle \left.-\,\left[2\exp \left(-\frac{\unicode[STIX]{x1D6E5}E}{k_{B}T_{w}}\right)-1\right]n_{2}\right\}-\frac{n_{3}}{\unicode[STIX]{x1D70F}_{D_{2}}}\nonumber\\ \displaystyle & & \displaystyle -\,2k_{EP3}(n_{3})^{2}-k_{PI}n_{3}n_{4},\nonumber\\ \displaystyle \frac{\text{d}n_{4}}{\text{d}t} & = & \displaystyle k_{EP2}\cdot (n_{2})^{2}+k_{EP3}\cdot (n_{3})^{2}-\frac{n_{4}}{\unicode[STIX]{x1D70F}_{4}}\nonumber\\ \displaystyle & & \displaystyle -\,k_{PI}n_{4}(n_{2}+n_{3})-\unicode[STIX]{x1D6E4}_{\text{photo-ionization}}\nonumber\\ \displaystyle & & \displaystyle +\,k_{\text{recombination}}(n_{5})^{3},\nonumber\\ \displaystyle \frac{\text{d}n_{5}}{\text{d}t} & = & \displaystyle k_{PI}n_{4}(n_{2}+n_{3})+\unicode[STIX]{x1D6E4}_{\text{photo-ionization}}\nonumber\\ \displaystyle & & \displaystyle -\,k_{\text{recombination}}(n_{5})^{3},\nonumber\\ \displaystyle \unicode[STIX]{x1D6E4}_{\text{photo-ionization}} & = & \displaystyle n_{4}\unicode[STIX]{x1D70E}_{\text{photo-ionization}}\left(\frac{I_{l}}{hv_{l}}+\frac{I_{P}}{hv_{p}}\right),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\text{d}n_{1}}{\text{d}t} & = & \displaystyle -\unicode[STIX]{x1D6E4}_{P}+\unicode[STIX]{x1D6E4}_{L}+\frac{n_{2}}{\unicode[STIX]{x1D70F}_{D_{1}}}+\frac{n_{3}}{\unicode[STIX]{x1D70F}_{D_{2}}}+\frac{n_{4}}{\unicode[STIX]{x1D70F}_{4}}\nonumber\\ \displaystyle & & \displaystyle +\,k_{EP2}(n_{2})^{2}+k_{EP3}(n_{3})^{2}\nonumber\\ \displaystyle & & \displaystyle +\,k_{PI}n_{4}(n_{2}+n_{3}),\nonumber\\ \displaystyle \frac{\text{d}n_{2}}{\text{d}t} & = & \displaystyle -\unicode[STIX]{x1D6E4}_{L}+\unicode[STIX]{x1D6FE}_{32}(T_{w})\left\{\vphantom{\left[2\exp \left(-\frac{\unicode[STIX]{x1D6E5}E}{k_{B}T_{w}}\right)-1\right]}[n_{3}-n_{2}]\right.\nonumber\\ \displaystyle & & \displaystyle \left.-\,\left[2\exp \left(-\frac{\unicode[STIX]{x1D6E5}E}{k_{B}T_{w}}\right)-1\right]n_{2}\right\}-\frac{n_{2}}{\unicode[STIX]{x1D70F}_{D_{1}}}\nonumber\\ \displaystyle & & \displaystyle -\,2k_{EP2}(n_{2})^{2}-k_{PI}n_{2}n_{4},\nonumber\\ \displaystyle \frac{\text{d}n_{3}}{\text{d}t} & = & \displaystyle \unicode[STIX]{x1D6E4}_{P}-\unicode[STIX]{x1D6FE}_{32}(T_{w})\left\{\vphantom{\left[2\exp \left(-\frac{\unicode[STIX]{x1D6E5}E}{k_{B}T_{w}}\right)-1\right]}[n_{3}-n_{2}]\right.\nonumber\\ \displaystyle & & \displaystyle \left.-\,\left[2\exp \left(-\frac{\unicode[STIX]{x1D6E5}E}{k_{B}T_{w}}\right)-1\right]n_{2}\right\}-\frac{n_{3}}{\unicode[STIX]{x1D70F}_{D_{2}}}\nonumber\\ \displaystyle & & \displaystyle -\,2k_{EP3}(n_{3})^{2}-k_{PI}n_{3}n_{4},\nonumber\\ \displaystyle \frac{\text{d}n_{4}}{\text{d}t} & = & \displaystyle k_{EP2}\cdot (n_{2})^{2}+k_{EP3}\cdot (n_{3})^{2}-\frac{n_{4}}{\unicode[STIX]{x1D70F}_{4}}\nonumber\\ \displaystyle & & \displaystyle -\,k_{PI}n_{4}(n_{2}+n_{3})-\unicode[STIX]{x1D6E4}_{\text{photo-ionization}}\nonumber\\ \displaystyle & & \displaystyle +\,k_{\text{recombination}}(n_{5})^{3},\nonumber\\ \displaystyle \frac{\text{d}n_{5}}{\text{d}t} & = & \displaystyle k_{PI}n_{4}(n_{2}+n_{3})+\unicode[STIX]{x1D6E4}_{\text{photo-ionization}}\nonumber\\ \displaystyle & & \displaystyle -\,k_{\text{recombination}}(n_{5})^{3},\nonumber\\ \displaystyle \unicode[STIX]{x1D6E4}_{\text{photo-ionization}} & = & \displaystyle n_{4}\unicode[STIX]{x1D70E}_{\text{photo-ionization}}\left(\frac{I_{l}}{hv_{l}}+\frac{I_{P}}{hv_{p}}\right),\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D6E4}_{P}$
is the stimulated absorption transition rate caused by pump photons,
$\unicode[STIX]{x1D6E4}_{P}$
is the stimulated absorption transition rate caused by pump photons,
![]() $\unicode[STIX]{x1D6E4}_{L}$
is the transition rate of laser emission,
$\unicode[STIX]{x1D6E4}_{L}$
is the transition rate of laser emission,
![]() $\unicode[STIX]{x1D6E4}_{\text{photo-ionization}}$
is the transition rate of photo-ionization,
$\unicode[STIX]{x1D6E4}_{\text{photo-ionization}}$
is the transition rate of photo-ionization,
![]() $\unicode[STIX]{x1D6FE}_{32}(T_{w})$
is the fine-structure relaxation rate,
$\unicode[STIX]{x1D6FE}_{32}(T_{w})$
is the fine-structure relaxation rate,
![]() $\unicode[STIX]{x1D6E5}E$
is the energy gap between the
$\unicode[STIX]{x1D6E5}E$
is the energy gap between the
![]() $^{2}P_{3/2}$
and
$^{2}P_{3/2}$
and
![]() $^{2}P_{1/2}$
levels with the value of
$^{2}P_{1/2}$
levels with the value of
![]() $554~\text{cm}^{-1}$
,
$554~\text{cm}^{-1}$
,
![]() $k_{B}$
is the Boltzmann constant,
$k_{B}$
is the Boltzmann constant,
![]() $\unicode[STIX]{x1D70F}_{D1}$
is the
$\unicode[STIX]{x1D70F}_{D1}$
is the
![]() $D_{1}$
(
$D_{1}$
(
![]() $6^{2}P_{1/2}\rightarrow 6^{2}S_{1/2}$
) radiative lifetime,
$6^{2}P_{1/2}\rightarrow 6^{2}S_{1/2}$
) radiative lifetime,
![]() $\unicode[STIX]{x1D70F}_{D2}$
is the
$\unicode[STIX]{x1D70F}_{D2}$
is the
![]() $D_{2}$
(
$D_{2}$
(
![]() $6^{2}S_{1/2}\rightarrow 6^{2}P_{3/2}$
) radiative lifetime,
$6^{2}S_{1/2}\rightarrow 6^{2}P_{3/2}$
) radiative lifetime,
![]() $\unicode[STIX]{x1D70E}_{\text{photo-ionization}}$
is the photo-ionization transverse section,
$\unicode[STIX]{x1D70E}_{\text{photo-ionization}}$
is the photo-ionization transverse section,
![]() $k_{EP2}(n_{2})^{2}$
denotes the transition rate of electrons from the
$k_{EP2}(n_{2})^{2}$
denotes the transition rate of electrons from the
![]() $6^{2}P_{1/2}$
to the
$6^{2}P_{1/2}$
to the
![]() $6^{2}D_{5/2,3/2}$
and
$6^{2}D_{5/2,3/2}$
and
![]() $8^{2}S_{1/2}$
levels,
$8^{2}S_{1/2}$
levels,
![]() $k_{EP3}(n_{3})^{2}$
denotes the transition rate from the
$k_{EP3}(n_{3})^{2}$
denotes the transition rate from the
![]() $6^{2}P_{3/2}$
level to the
$6^{2}P_{3/2}$
level to the
![]() $6^{2}D_{5/2,3/2}$
and
$6^{2}D_{5/2,3/2}$
and
![]() $8^{2}S_{1/2}$
levels,
$8^{2}S_{1/2}$
levels,
![]() $k_{PI}$
is the Penning ionization rate coefficients,
$k_{PI}$
is the Penning ionization rate coefficients,
![]() $k_{\text{recombination}}$
is the recombination rate constant,
$k_{\text{recombination}}$
is the recombination rate constant,
![]() $I_{P}$
and
$I_{P}$
and
![]() $I_{l}$
are the pump and laser intensities given by Ref. [Reference Steck12] and
$I_{l}$
are the pump and laser intensities given by Ref. [Reference Steck12] and
![]() $\unicode[STIX]{x1D70F}_{4}$
is the lifetime of
$\unicode[STIX]{x1D70F}_{4}$
is the lifetime of
![]() $6^{2}D_{5/2,3/2}$
and
$6^{2}D_{5/2,3/2}$
and
![]() $8^{2}S_{1/2}$
levels[Reference Knize, Zhdanov and Shaffer13], respectively. Note that we assume the lifetimes of
$8^{2}S_{1/2}$
levels[Reference Knize, Zhdanov and Shaffer13], respectively. Note that we assume the lifetimes of
![]() $6^{2}D_{5/2,3/2}$
and
$6^{2}D_{5/2,3/2}$
and
![]() $8^{2}S_{1/2}$
levels are of the same value to simplify the calculation. A summary of critical parameters of this model are listed in Table 1. Note that the transmission loss of the hollow-core fiber is set to 0.82 in the theoretical calculation.
$8^{2}S_{1/2}$
levels are of the same value to simplify the calculation. A summary of critical parameters of this model are listed in Table 1. Note that the transmission loss of the hollow-core fiber is set to 0.82 in the theoretical calculation.
Table 1. Summary of critical parameters in our model.

3 Results and discussions
To systematically investigate the influence of deleterious processes on the physical features of a DPAL, we list five cases in Table 2. Case 1 denotes a simple three-level system investigated in the absence of excitation to the upper states
![]() $6^{2}D_{5/2,3/2}$
and
$6^{2}D_{5/2,3/2}$
and
![]() $8^{2}S_{1/2}$
and their ionization. Case 2 represents the state with considering the process of energy pooling. Case 3 describes the processes of energy pooling and Penning ionization. Case 4 illustrates the occurrence when energy pooling and photo-ionization are considered. Case 5 reflects the circumstance including all of these three processes.
$8^{2}S_{1/2}$
and their ionization. Case 2 represents the state with considering the process of energy pooling. Case 3 describes the processes of energy pooling and Penning ionization. Case 4 illustrates the occurrence when energy pooling and photo-ionization are considered. Case 5 reflects the circumstance including all of these three processes.
Table 2. Different cases investigated in the model.

In Figure 3, the laser power is given as a function of the pump power. It can be seen that all the quantities of the curves monotonically increase with the pump level when the pump power is less than 50 W. When the pump power exceeds 50 W, the output powers of Cases 1–5 reach a plateau since the pump absorption already achieves the saturated status in an HC-PCF cell. In addition, different curves in Figure 3 show the contribution of different processes to the output power. Comparing the curve of Case 1 with that of Case 2, there is almost no difference between them, which indicates that the process of energy pooling has little influence on the output power. For the curves of Cases 3 and 4, the output decreases are 1.92% and 13.90% with the pump power of 100 W, respectively. The reason of this is the decrease of the number density of neutral alkali atoms caused by the process of ionization. Further, when considering both processes of Penning ionization and photo-ionization in the model (Case 5), the curve decreases by 13.92% with the pump power of 100 W. This result suggests that photo-ionization provide greater influence than Penning ionization.

Figure 3. Output power versus pump power in different cases.
Figure 4 shows the absorbed power, output power, and optical-to-optical efficiency as functions of the pump power when the temperature is set to
![]() $110\,^{\circ }\text{C}$
. As shown in Figure 4, the maximal optical-to-optical efficiency can be obtained at pump power of 50 W in both Cases 1 and 5. In the range of 50–100 W for pump power, the optical-to-optical efficiency decreases with increase of the pump power due to the saturation of output power. Further, the maximal optical-to-optical efficiency of Case 5 (64.87%) is lower than that of Case 1 (71.72%) because of the effect of deleterious processes.
$110\,^{\circ }\text{C}$
. As shown in Figure 4, the maximal optical-to-optical efficiency can be obtained at pump power of 50 W in both Cases 1 and 5. In the range of 50–100 W for pump power, the optical-to-optical efficiency decreases with increase of the pump power due to the saturation of output power. Further, the maximal optical-to-optical efficiency of Case 5 (64.87%) is lower than that of Case 1 (71.72%) because of the effect of deleterious processes.

Figure 4. Absorbed power, output power, and optical-to-optical efficiency versus pump power in (a) Case 1 and (b) Case 5.
Unlike other types of lasers, the density of a gas-state gain medium inside the hollow fiber is extremely sensitive to the ambient temperature[Reference Sulham, Perram, Wilkinson and Hostutler18]. In Figure 5, the absorbed power, output power, and population density are given as functions of the fiber temperature. The fiber length and pump power are set to 2 m and 100 W, respectively. It can be seen that the population density increases with the temperature in Figure 5. However, saturation occurs at the temperature higher than
![]() $120\,^{\circ }\text{C}$
for the curves corresponding to both the absorbed power and the output power. It means that the absorbed power or the output power cannot be greatly improved when the temperature is higher than
$120\,^{\circ }\text{C}$
for the curves corresponding to both the absorbed power and the output power. It means that the absorbed power or the output power cannot be greatly improved when the temperature is higher than
![]() $120\,^{\circ }\text{C}$
although the total population density is exponentially increased inside the hollow fiber. To further increase the output power above
$120\,^{\circ }\text{C}$
although the total population density is exponentially increased inside the hollow fiber. To further increase the output power above
![]() $120\,^{\circ }\text{C}$
, the pump power should be enhanced.
$120\,^{\circ }\text{C}$
, the pump power should be enhanced.

Figure 5. Absorbed power, output power, and population density (
![]() $n_{0}$
) versus temperature of Case 1.
$n_{0}$
) versus temperature of Case 1.
4 Summary
In this study, we develop a mathematical model to calculate the static-state DPALs using an HC-PCF as the vapor cell. The effect of deleterious processes including energy pooling, Penning ionization, and photo-ionization on the output features of a DPAL are theoretically investigated. We also study how the temperature influences the output power and alkali population. The results reveal that the output power will decrease because of the deleterious processes, and such a phenomenon becomes serious with the even higher pump power. It has also been found that the density of the alkali vapor inside the fiber cell is extremely sensitive to the ambient temperature. In other words, the temperature is a critical factor in this new kind of laser system.









