Effects of side subsurface defects induced by CNC machine on the gain spatial distribution in neodymium phosphate glass

Abstract

The processing method applied to the side surface is different from the method applied to the light pass surface in neodymium phosphate glass (Nd:glass), and thus subsurface defects remain after processing. The subsurface defects in the side surface influence the gain uniformity of Nd:glass, which is a key factor to evaluate the performance of amplifiers. The scattering characteristics of side subsurface defects were simulated by finite difference time domain (FDTD) Solutions software. The scattering powers of the glass fabricated by a computer numerical control (CNC) machine without cladding were tested at different incident angles. The trend of the curve was similar to the simulated result, while the smallest point was different with the complex true morphology. The simulation showed that the equivalent residual reflectivity of the cladding glass can be more than 0.1% when the number of defects in a single gridding is greater than 50.

1 Introduction

A disk amplifier pumped by flash lamps is the primary main amplifier in lasers at the mega joule (MJ) level. Beamlet^[1], the National Ignition Facility (NIF)^[2] developed by Livermore in America, the LMJ^[3] building at French Atomic Energy Commission, SG II^[4] and SG III^[5] in China are the typical MJ lasers, in which disk amplifiers are employed to magnify energy. The main gain medium in disk amplifiers is neodymium phosphate glass (Nd:glass)^[6], whose energy conversion efficiency determines the gain of the amplifier directly. When clear aperture is increased, the amplified spontaneous emission (ASE) and parasitic oscillation (PO) decrease the gain uniformity of Nd:glass intensely^[7]. In order to suppress the ASE and PO, cladding is used on the side of the glass^{[8, 9]}. There are many ways to realize cladding, for example, sealing cladding^[10], liquid cladding^[11], polymer edge cladding^[12], thin film coatings^[13], and so on. The research on cladding has focused on the structures of cladding, while the influences of the defects induced by the process of glass on the properties of cladding have been less well studied.

The Nd:glass manufactured by continuous melting is made to a specific size after cutting, grinding and polishing. During the process, forces act on the surface of the optical element and introduce scratches and micro cracks which are called subsurface defects. This paper mainly discusses the defects near the interface of the gain medium in amplifiers where damage rarely occurs, and thus the term ‘subsurface defect’ is used instead of ‘subsurface damage’. The subsurface defects reduce the laser-induced damage threshold (LIDT), and affect the mechanical and scattering properties. To decrease the subsurface defects in optical glass, step-by-step classic processing is applied to process the light pass surface of Nd:glass^[14], and the cracks left in the glass have micron or submicron dimensions^[15]. The side of the glass is processed by a computer numerical control (CNC) machine because of its large length–width ratio, and subsurface defects remain near the surface^[16]. The greater the size of the glass , the more rigorous the process of the side surface is. The side subsurface defects scatter some of the ASE flux back into the glass, which then consumes more of the inversion population and influences the gain. It is imperative to consider subsurface defects when simulating the gain distribution. Polarized light was used by Marcus et al. ^[17] to measure the scattered light from subsurface defect at different scattering angles. An integrating sphere was employed by Zhang et al. ^[18] to test the transmission properties of a silicon layer and a 2D scattering sphere was used to evaluate the scattering from subsurface defects. While the results of these experiments are the scattered light obtained from outside of the glass, all scattered light introduced by the subsurface defect is necessary. The Rayleigh scattering or Mie scattering model can be used to solve for scattering intensity of particle^[19]. However, the morphology of subsurface defects is irregularity, and thus a particle scattering model is not suitable. The finite difference time domain method (FDTD) solve for the electric field distribution with a defect, and has been used to obtain the light intensity enhancement factor (LIEF) to explore the nature of laser-induced damage^[20–23]. The morphology of the subsurface defect can be set randomly using FDTD, and thus FDTD Solutions was employed to analyze the scattering intensity induced by side subsurface defects at different incident angles. The scattering power of glass processed by a CNC machine was measured. The equivalent residual reflectivity is proposed to evaluate the influence of the subsurface defects on the gain of Nd:glass.

2 Structures of Nd:glass with cladding

The polymer edge cladding proposed by Campbell^[12] in 1986 is universally used in the cladding of Nd:glass because it is easy to produce in quantity. A cladding glass with Cu$^{2+}$ ions adheres to the side of Nd:glass with a polymer such as epoxy. The structure of Nd:glass with cladding is shown in Figure 1.

Figure 1. Structure of Nd:glass with cladding.

The refractive indexes of Nd:glass, the glue and the cladding glass satisfy the index matching condition, for example 1.528, 1.534, 1.536, respectively. The cladding glass is used to suppress the reflection of ASE and absorb ASE when it enters the cladding glass at random incident angles. The residual reflectivity of the cladding glass is the main index to assess the quality of cladding.

3 Geometric modeling of the defects after processing

The defects in the glass after grinding and polishing are mainly of two types depending on the generation mechanisms^[24]. One is brittle fracture, and the other is plastic deformation. Plastic deformation occurs when the stress is small, so the plastic scratch has the features of abrasive particles. The crack becomes a brittle crack with the increase in stress. The typical defect after polishing is a plastic scratch, whose depth is smaller than width. Some brittle fractures also remain after the polishing process. The main defects discussed in this paper are plastic scratches using 2D FDTD simulation, because polishing is usually the last step in the processing of glass.

The typical plastic scratch morphology^[25] is shown in Figure 2.

Figure 2. Morphology of plastic scratch.

Here, $w$ and $d$ are the width and depth of the defect, respectively. The scattering intensity induced by the defect changes with the polarization of the incident light, the morphology of the defects and the rear or front of the surface. The scattered ASE amounts the situation that the light starts in the glass and propagates in the glass then reaches the defects near the surface of the glass.

A simulation result is more accurate with smaller simulation region gridding, meanwhile more time is needed. There are two conditions for setting the gridding:

1. (1) courant stability condition

   (1)$$\begin{eqnarray}{\it\nu}\times {\rm\Delta}t\leqslant \frac{1}{\sqrt{\left(\frac{1}{{\rm\Delta}x}\right)^{2}+\left(\frac{1}{{\rm\Delta}y}\right)^{2}}},\end{eqnarray}$$

2. (2) numerical dispersion

   (2)$$\begin{eqnarray}{\rm\Delta}_{\max }<{\it\lambda}_{\min }/10.\end{eqnarray}$$

The parameter ${\it\nu}$ is the transmission speed in the medium, ${\rm\Delta}t$ is the time interval, ${\rm\Delta}x,{\rm\Delta}y$ is the space interval, ${\rm\Delta}_{\max }$ is the greatest space interval selected in the simulation and ${\it\lambda}_{\min }$ is the smallest wavelength of incident light. In the simulation, ${\it\lambda}_{\min }$ was 1053 nm.

4 Defect scattering induced by the CNC machine

4.1 Simulation

The size and morphology of the defects after polishing depends on the polishing abrasives, the load, and so on. The greater size of the defect, the larger amount of light scattered. The plastic scratch induced by the CNC machine according to Refs. [26–28] was modeled to calculate the scattering of defect. The simulated defect is shown in Figure 3, where ${\it\theta}$ represents the incident angles of the input light.

Figure 3. Morphology of the plastic scratch.

The FDTD region was $100~{\rm\mu}\text{m}\times 18~{\rm\mu}\text{m}$. The space intervals in $x$ and $y$ direction were both $0.02~{\rm\mu}\text{m}$. The calculated time was 1000 fs. The setting of the parameters satisfied the courant stability condition and the numerical dispersion. The refractive indexes of the Nd:glass and the cladding are 1.528 and 1.536.

The scattering ratio $R_{\text{sca}}$ which is the normalized scattering intensity at different incident angles ${\it\theta}$ is shown in Figure 4.

Figure 4. Changes in normalized scattering intensity at different incident angles.

The scattering ratio range were [0.0241, 0.3283] and [0.0223, 0.3342] for $s$- and $p$-polarized waves, respectively. The scattering changed with incident angles but was symmetrical for the simulated symmetrical structure. The greatest scattering ratio occurred near $20^{\circ }$ and $160^{\circ }$, while the smallest scattering ratio occurred near $90^{\circ }$. The scattering from the subsurface defect can be explained using the interference of light. A plane wave is assumed to pass through the medium. When the light meets the defect, the light can be reflected or refracted depending on the incident angle. When the light reflected form the interface of the defects, the incident light and the light reflected from the interface between the cladding and the Nd:glass meet, an interference occurs and the electric field is changed with some enhancement and some decrease^[21]. Compared with the primary field, the electric field has a different distribution which is the sum of the incident field and the scattering field.

4.2 Experiment

The scattering caused by subsurface defects is multiple scattering whose polarization can change at the input surface^[17]. The polarization of scattering induced by roughness is unchangeable at the input surface and the scattering intensity is much smaller compared with subsurface defects when the incident light is $p$-polarized^[17]. The polarization method was used to measure the scattering powers caused by subsurface defects at different incident angles. The structure without cladding was used for ease of measure, whose trend is similar to the situation with cladding but the values are mildly different in simulation.

Two glasses with a diameter of 50 mm and thickness of 10 mm were prepared: Samples A and B. Sample A was processed by step-by-step classic processing; while one side of the Sample B was processed by the CNC machine, the other side was processed by step-by-step classic processing.

The schematic of the experiment is shown in Figure 5. The input light was $s$-polarized with a wavelength of 1053 nm.

Figure 5. Schematic diagram of the experimental setup.

In Figure 5, $f_{1}$ is a lens whose function is to make the incident light parallel, and the functions of lenses $f_{2}$ and $f_{3}$ are focusing the light into the detectors. Two polarization splitting prisms (PBSs), a half wavelength plate and a diaphragm are needed in the experiment setup. The sample is put onto the center of a 3D control platform. Knocking the axle wire of the sample, the position of the output light was unchanged by moving the input point.

The two detectors recorded the output powers of the $s$- and $p$-polarized waves. The incident light was $p$-polarized after passing through the half wavelength plate, and thus, when the scattering at the subsurface defect occurred, the $s$-polarized power could be recorded.

The light passed through Samples A and B at different incident angles ${\it\theta}$ successively. The scattering power $P_{\text{sca}}$ obtained was the difference between the two sets of data measured with Samples A and B. The measured curve is shown in Figure 6.

Figure 6. Scattering powers of glass at different incident angles.

Figure 7. (a) Average small signal gain coefficients and (b) gain uniformity of complete absorption and with residual reflection in cladding.

The scattering power of glass showed a trend similar to that of the simulation result. The smallest value occurred at different incident angles because the morphology of subsurface defects in the real glass was more complex than that in the simulated one, the tested point might have contained some brittle fractures, and so on.

5 Side subsurface defects effects the gain of Nd:glass

The side of Nd:glass used in the disk amplifier is generally processed by a CNC machine, and thus, the defect modeled was assumed to be within the side of the glass. Some light that can reach and be absorbed by the cladding glass is scattered by the defects. Then, the scattered light traverses the gain medium again to consume the inversion population. The polarization state of ASE flux traveling in the medium is random, so the ASE assumed to be half $s$-polarized and half $p$-polarized. According to Section 4.1, the scattering ratio was [0.0232, 0.3305]. The calculated region was $100~{\rm\mu}\text{m}\times 13.9~{\rm\mu}\text{m}$ except for the $2~{\rm\mu}\text{m}$ cladding glass, $2~{\rm\mu}\text{m}$ air and $0.1~{\rm\mu}\text{m}$ light source. Using Monte Carlo, a procedure was accomplished to calculate the gain spatial distribution of Nd:glass with cladding^[29]. The small signal gain coefficient and gain uniformity with different residual reflectivity are shown in Figure 7, where $f$ is the residual reflectivity of cladding glass.

The abscissas are the logarithm of the residual reflectivity which are 0.01%, 0.05%, 0.1%, 1% and 5%. When the residual reflectivity of the cladding glass is bigger than 0.1%, the small signal gain coefficient $g_{\text{ave}}$ and the gain uniformity decrease rapidly. The gain uniformity is the ratio of the maximum gain coefficient and the average gain coefficient, and thus the gain uniformity is better when the ratio is small.

The size of the gain medium and the single gridding were $68.2~\text{cm}\times 36.3~\text{cm}\times 4.5~\text{cm}$ and $1.364~\text{cm}\times 0.726~\text{cm}\times 0.18~\text{cm}$^[29], respectively. The scattering in a 2D single gridding is shown in Figure 8.

Figure 8. Map of the single gridding region with subsurface defect.

The scattering ratio range in a 2D single gridding was $[0.1313\times 10^{-3}\%,0.1871\times 10^{-2}\%]$. The distribution of subsurface defects was assumed to be uniform after processing the entire optical surface. The residual reflectivity of the cladding glass without defects was assumed to be 0.05%, and thus the equivalent residual reflectivity with a defect was [0.0501%, 0.0519%]. One subsurface defect in a single gridding had less influence on the performance of the gain in the glass.

The subsurface defects induced in the Nd:glass after processing were more than one in a single gridding. Assuming that $n$ subsurface defects exist in a single gridding, the equivalent residual reflectivity was $[(0.05+0.1313\times 10^{-3}\times n)\%,(0.05+0.1871\times 10^{-2}\times n)\%]$, in which effects between subsurface defects are ignored. The equivalent residual reflectivity varying with $n$ is shown in Figure 9.

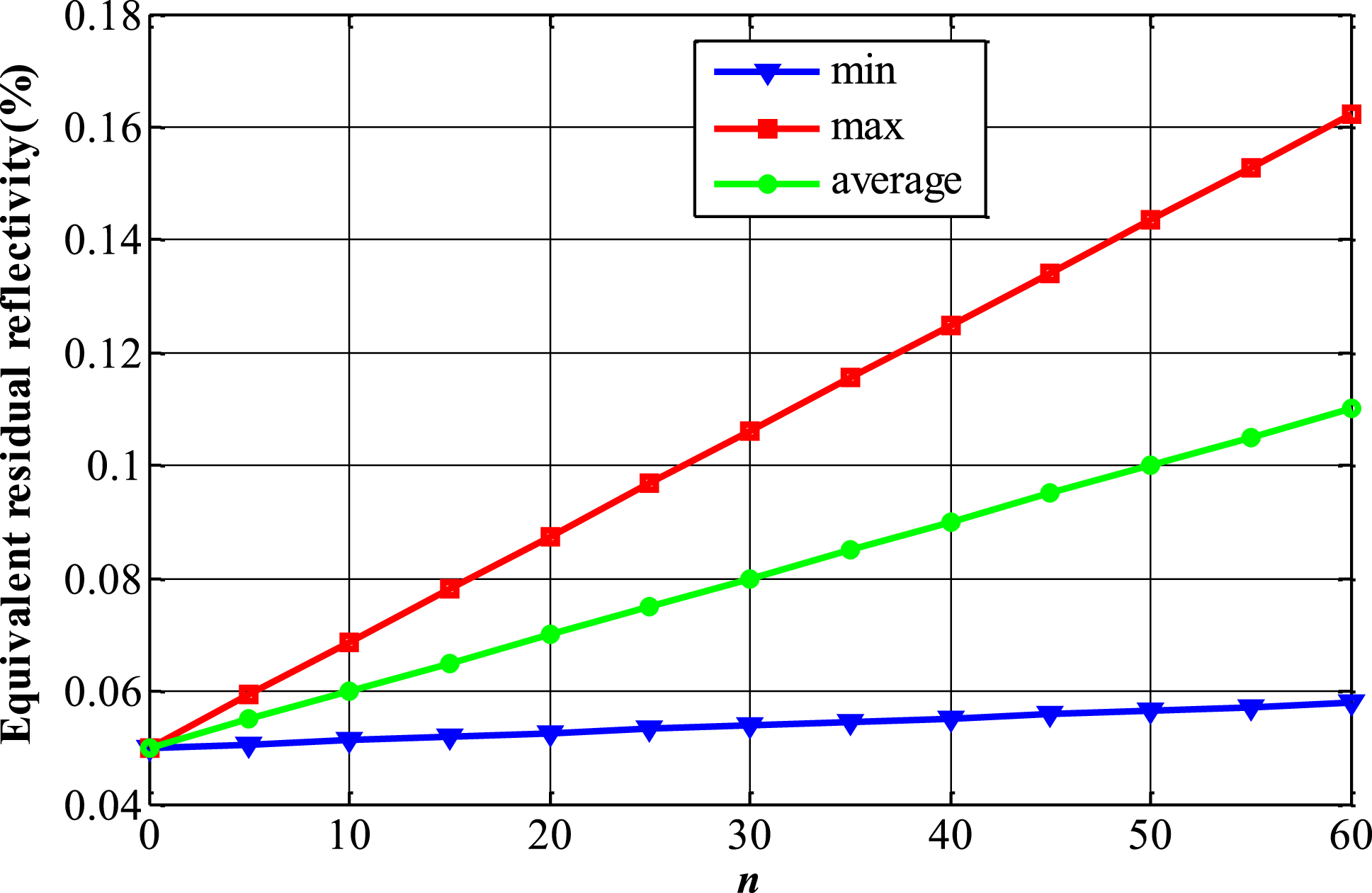
Figure 9. Equivalent residual reflectivity with the change of $n$.

The curves ‘max’ and ‘min’ indicate the greatest and smallest equivalent residual reflectivity for the different $n$. The curve ‘average’ is the average value of the greatest and smallest value for the same $n$. The average equivalent residual reflectivity was used to assess the effect of subsurface defects. For the simulated defect, the average equivalent residual reflectivity was up to 0.1% with 50 scratches in a single gridding. The subsurface defect in the clear aperture produced by step-by-step classical processing was small, which can be calculated using the same method.

6 Conclusions

The scattering characteristics of the side subsurface defects after CNC machine at different incident angles were simulated by FDTD Solutions. The scattering powers at different incident angles were measured by polarization method, which showed a similar trend with the simulated results while the minimum values varied with the real morphology of the tested defect. The results showed that the scattering from side subsurface defects can make the residual reflectivity be more than 0.1% when the number of defects is greater than 50 in a single gridding, which can decrease the gain and gain uniformity obviously. The method for decreasing the influences of subsurface defects in the side of Nd:glass involves two aspects. One is applying more advanced processing methods, such as magneto rheological finishing (MRF), while the other is disposing the processed optical elements, such as hydrofluoric acid, which can eliminate or decrease the subsurface defects and will be studied in future works.