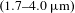1 Introduction
The development of mid-infrared (IR) ultrafast pulsed lasers of high intensity, short pulse duration and tunable carrier wavelength at  $2.0{-}5.0~\unicode[STIX]{x03BC}\text{m}$ is of great interest for a diverse range of applications from high harmonic generation[Reference Popmintchev, Chen, Popmintchev, Arpin, Brown, Alisauskas, Andriukaitis, Balciunas, Mücke, Pugzlys, Baltuska, Shim, Schrauth, Gaeta, Hernandez-Garcia, Plaja, Becker, Jaron-Becker, Murnane and Kapteyn1, Reference Ghimire and Reis2] and laser wakefield acceleration[Reference Kim, Pae, Cha, Kim, Yu, Sung, Lee, Jeong and Lee3, Reference Woodbury, Feder, Shumakova, Gollner, Schwartz, Miao, Salehi, Korolov, Pugžlys, Baltuška and Milchberg4] to spectroscopic investigation[Reference Keilmann, Gohle and Holzwarth5, Reference Cha, Sung, Sim, Park, Heo, Jo and Choi6]. Owing to the lack of proper gain media, nonlinear down-conversion is a common method to generate the intensive mid-IR pulsed laser, which is inaccessible by a mode-locked laser. Particularly, with the advantages of ultra-broadband amplification and wavelength tunability, the broadband optical parametric amplification (OPA) or difference frequency generation (DFG) between two traditional near-IR pulsed lasers has been widely exploited[Reference Zhao, Zhong, Yuan, Xie, Wang, Ma and Qian7–Reference Ishii, Xia, Kanai and Itatani9]. However, there are essential obstacles in the pursuit of greater pulse energy and shorter pulse duration. On one hand, in standard femtosecond OPA/DFG systems, the pump and signal pulses are both Fourier-transform-limited (TL)[Reference Cerullo and Silvestri10]. Restricted by the ubiquitous group-velocity mismatch (GVM) of the interacting waves and the damage threshold of the nonlinear media, only confined crystal length and pump intensity are acceptable, which will inevitably lead to an inefficient energy transfer process. On the other hand, the mid-IR pulsed laser primarily originates from the nonlinear down-conversion between two temporally synchronized pulsed lasers; as a result, its bandwidth may also be inferior to those of the driving lasers[Reference Andriukaitis, Balčiūnas, Ališauskas, Pugžlys, Baltuška, Popmintchev, Chen, Murnane and Kapteyn11, Reference Pupeza, Sánchez, Zhang, Lilienfein, Seidel, Karpowicz, Paasch-Colberg, Znakovskaya, Pescher, Schweinberger, Pervak, Fill, Pronin, Wei, Krausz, Apolonski and Biegert12].
$2.0{-}5.0~\unicode[STIX]{x03BC}\text{m}$ is of great interest for a diverse range of applications from high harmonic generation[Reference Popmintchev, Chen, Popmintchev, Arpin, Brown, Alisauskas, Andriukaitis, Balciunas, Mücke, Pugzlys, Baltuska, Shim, Schrauth, Gaeta, Hernandez-Garcia, Plaja, Becker, Jaron-Becker, Murnane and Kapteyn1, Reference Ghimire and Reis2] and laser wakefield acceleration[Reference Kim, Pae, Cha, Kim, Yu, Sung, Lee, Jeong and Lee3, Reference Woodbury, Feder, Shumakova, Gollner, Schwartz, Miao, Salehi, Korolov, Pugžlys, Baltuška and Milchberg4] to spectroscopic investigation[Reference Keilmann, Gohle and Holzwarth5, Reference Cha, Sung, Sim, Park, Heo, Jo and Choi6]. Owing to the lack of proper gain media, nonlinear down-conversion is a common method to generate the intensive mid-IR pulsed laser, which is inaccessible by a mode-locked laser. Particularly, with the advantages of ultra-broadband amplification and wavelength tunability, the broadband optical parametric amplification (OPA) or difference frequency generation (DFG) between two traditional near-IR pulsed lasers has been widely exploited[Reference Zhao, Zhong, Yuan, Xie, Wang, Ma and Qian7–Reference Ishii, Xia, Kanai and Itatani9]. However, there are essential obstacles in the pursuit of greater pulse energy and shorter pulse duration. On one hand, in standard femtosecond OPA/DFG systems, the pump and signal pulses are both Fourier-transform-limited (TL)[Reference Cerullo and Silvestri10]. Restricted by the ubiquitous group-velocity mismatch (GVM) of the interacting waves and the damage threshold of the nonlinear media, only confined crystal length and pump intensity are acceptable, which will inevitably lead to an inefficient energy transfer process. On the other hand, the mid-IR pulsed laser primarily originates from the nonlinear down-conversion between two temporally synchronized pulsed lasers; as a result, its bandwidth may also be inferior to those of the driving lasers[Reference Andriukaitis, Balčiūnas, Ališauskas, Pugžlys, Baltuška, Popmintchev, Chen, Murnane and Kapteyn11, Reference Pupeza, Sánchez, Zhang, Lilienfein, Seidel, Karpowicz, Paasch-Colberg, Znakovskaya, Pescher, Schweinberger, Pervak, Fill, Pronin, Wei, Krausz, Apolonski and Biegert12].
Previously, Zhang et al. reported an OPA scheme termed dual-chirped optical parametric amplification (DC-OPA)[Reference Zhang, Takahashi, Mücke, Lu and Midorikawa13, Reference Fua, Xue, Midorikawa and Takahashi14], where both the pump and signal waves are temporally stretched. The prolonged laser pulses may relieve the influence of pulse slipping owing to the nonuniform group velocities. In addition, the broadband spectrum of the pump wave may even be utilized to fulfill the broadband phase-matching (PM) amplification. Compared to its chirp-free counterpart, it provides an additional degree of freedom to regulate the spectrum of the generated idler wave[Reference Fu, Takahashi, Zhang, Lu and Midorikawa15]. Specifically, when the chirp signs of the pump and the signal waves are opposite, a remarkably broadened idler wave may be generated. Similar nonlinear techniques were successfully applied for the broadband second-harmonic generation and frequency tripling, or the generation of narrow-bandwidth picosecond pulses[Reference Raoult, Boscheron, Husson, Rouyer, Sauteret and Migus16–Reference Luo, Qian, Yuan and Zhu18]. However, broadband PM is always the prerequisite for efficient energy boosting and circumvention of the GVM-associated gain-narrowing effect. Evidently, to satisfy the broadband PM condition, the instantaneous wave vectors should be properly arranged into pairs to constantly meet the PM conditions[Reference Fu, Takahashi, Zhang, Lu and Midorikawa15, Reference Li, Liang, Dai, Yang, Zhong and Fan19].
In this study, specific to an oppositely dual-chirped DFG scheme, we derive the precondition to realize broadband frequency conversion. Then, to select the proper nonlinear crystals for various parametric processes, we systematically analyze the group-velocity relationship and the gain spectra of different nonlinear crystals at different wavelengths. Thereinto, the periodically poled lithium niobate (PPLN) crystal that satisfies an inactive Type-II (eo-o) quasi-phase-matching (QPM) condition exhibits the required negative correlation coefficient of the group velocity and the expected broadband gain characteristics across an ultra-broad idler spectral region  $(1.7{-}4.0~\unicode[STIX]{x03BC}\text{m})$.
$(1.7{-}4.0~\unicode[STIX]{x03BC}\text{m})$.
Excellent experimental works have been reported on the generation of few-cycle mid-IR pulses. Resorting to a traditional noncollinear PM geometry or a well-designed aperiodic QPM crystal, broadband mid-IR pulsed lasers are directly generated as the idler of a difference frequency generator[Reference Mayer, Phillips, Gallmann and Keller20, Reference Mero and Petrov21]. However, a subsequent angular dispersion correction is generally necessary for the noncollinear DFG design, and an aperiodic QPM crystal is not convenient for realizing the idler wavelength tunability for the latter method. As presented, an oppositely dual-chirped DFG is capable of generating a spectrum-broadened idler seeding in combination with the broadband PM circumstances. It also allows for using a longer crystal and a lower intensity to achieve efficient energy transfer, which is beneficial to limit the negative  $\unicode[STIX]{x1D712}^{3}$ effects. On this basis, we propose and numerically verify a promising DFG configuration to construct a tunable mid-IR spectrum broader based on the broadband phase-matched oppositely dual-chirped DFG scheme.
$\unicode[STIX]{x1D712}^{3}$ effects. On this basis, we propose and numerically verify a promising DFG configuration to construct a tunable mid-IR spectrum broader based on the broadband phase-matched oppositely dual-chirped DFG scheme.
2 Broadband phase-matching condition
In a standard ultrafast OPA/DFG system, the pump and signal pulses are both nearly transform-limited. Nevertheless, prolonged pulse duration is advantageous to relaxing the ubiquitous pulse slipping, reducing the input power density to avoid unwanted disturbing phenomena and potentially providing the PM environment across a broad spectrum.

Figure 1. (a) Instantaneous angular frequencies  $(\unicode[STIX]{x1D714}_{p}(t),\unicode[STIX]{x1D714}_{s}(t))$ and the bandwidth of each interacting wave (
$(\unicode[STIX]{x1D714}_{p}(t),\unicode[STIX]{x1D714}_{s}(t))$ and the bandwidth of each interacting wave ( $\unicode[STIX]{x0394}\unicode[STIX]{x1D714}_{p}$,
$\unicode[STIX]{x0394}\unicode[STIX]{x1D714}_{p}$,  $\unicode[STIX]{x0394}\unicode[STIX]{x1D714}_{s}$,
$\unicode[STIX]{x0394}\unicode[STIX]{x1D714}_{s}$,  $\unicode[STIX]{x0394}\unicode[STIX]{x1D714}_{i}$) of the oppositely dual-chirped DFG scheme; (b) sketch of the ideal broadband PM condition.
$\unicode[STIX]{x0394}\unicode[STIX]{x1D714}_{i}$) of the oppositely dual-chirped DFG scheme; (b) sketch of the ideal broadband PM condition.
A simple qualitative picture of such a parametric process is given in Figure 1(a). Each frequency component of the pump and the signal waves is linearly distributed in the temporal domain. The instantaneous frequency can be respectively expressed as  $\unicode[STIX]{x1D714}_{p}(t)=\unicode[STIX]{x1D714}_{0p}+\unicode[STIX]{x1D6FC}_{p}t$ and
$\unicode[STIX]{x1D714}_{p}(t)=\unicode[STIX]{x1D714}_{0p}+\unicode[STIX]{x1D6FC}_{p}t$ and  $\unicode[STIX]{x1D714}_{s}(t)=\unicode[STIX]{x1D714}_{0s}+\unicode[STIX]{x1D6FC}_{s}t$, where
$\unicode[STIX]{x1D714}_{s}(t)=\unicode[STIX]{x1D714}_{0s}+\unicode[STIX]{x1D6FC}_{s}t$, where  $\unicode[STIX]{x1D714}_{0}$ and
$\unicode[STIX]{x1D714}_{0}$ and  $\unicode[STIX]{x1D6FC}$ represent the central frequency and the linear chirp coefficient. The parameters
$\unicode[STIX]{x1D6FC}$ represent the central frequency and the linear chirp coefficient. The parameters  $p$,
$p$,  $s$ and
$s$ and  $i$ indicate the pump, the signal and the idler wave, respectively. Then, the generated difference frequency (i.e., the idler wave) can be subsequently given by
$i$ indicate the pump, the signal and the idler wave, respectively. Then, the generated difference frequency (i.e., the idler wave) can be subsequently given by  $\unicode[STIX]{x1D714}_{i}(t)=\unicode[STIX]{x1D714}_{p}(t)-\unicode[STIX]{x1D714}_{s}(t)=\unicode[STIX]{x1D714}_{0i}+\unicode[STIX]{x1D6FC}_{i}t=\unicode[STIX]{x1D714}_{0i}+(\unicode[STIX]{x1D6FC}_{p}-\unicode[STIX]{x1D6FC}_{s})t$. In case the signs of
$\unicode[STIX]{x1D714}_{i}(t)=\unicode[STIX]{x1D714}_{p}(t)-\unicode[STIX]{x1D714}_{s}(t)=\unicode[STIX]{x1D714}_{0i}+\unicode[STIX]{x1D6FC}_{i}t=\unicode[STIX]{x1D714}_{0i}+(\unicode[STIX]{x1D6FC}_{p}-\unicode[STIX]{x1D6FC}_{s})t$. In case the signs of  $\unicode[STIX]{x1D6FC}_{p}$ and
$\unicode[STIX]{x1D6FC}_{p}$ and  $\unicode[STIX]{x1D6FC}_{s}$ are opposite, the generated idler wave may be significantly broadened, with an approximately doubled spectral bandwidth as the summation of the pump and the signal waves. However, phase mismatch is a common limitation to efficient broadband frequency conversion. For the presented chirp-assisted DFG process, a more demanding PM bandwidth is required to cover the potentially much broader idler spectrum. It is desirable that each instantaneous wave-vector pair can be perfectly phase-matched similarly to the central frequency pair, as shown in Figure 1(b).
$\unicode[STIX]{x1D6FC}_{s}$ are opposite, the generated idler wave may be significantly broadened, with an approximately doubled spectral bandwidth as the summation of the pump and the signal waves. However, phase mismatch is a common limitation to efficient broadband frequency conversion. For the presented chirp-assisted DFG process, a more demanding PM bandwidth is required to cover the potentially much broader idler spectrum. It is desirable that each instantaneous wave-vector pair can be perfectly phase-matched similarly to the central frequency pair, as shown in Figure 1(b).
Assuming that the pulsed lasers have been sufficiently stretched and the pulse envelope slipping is negligible, individual temporal slices (i.e., individual spectral components) of the pump and the signal waves are arranged in pairs. The instantaneous wave-vector mismatch of  $\unicode[STIX]{x0394}k(t)$ can be defined as
$\unicode[STIX]{x0394}k(t)$ can be defined as
 $$\begin{eqnarray}\unicode[STIX]{x0394}k(t)=k_{p}(\unicode[STIX]{x1D714}_{p}(t))-k_{s}(\unicode[STIX]{x1D714}_{s}(t))-k_{i}(\unicode[STIX]{x1D714}_{i}(t)),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x0394}k(t)=k_{p}(\unicode[STIX]{x1D714}_{p}(t))-k_{s}(\unicode[STIX]{x1D714}_{s}(t))-k_{i}(\unicode[STIX]{x1D714}_{i}(t)),\end{eqnarray}$$ where  $k(\unicode[STIX]{x1D714}_{p}(t))$,
$k(\unicode[STIX]{x1D714}_{p}(t))$,  $k(\unicode[STIX]{x1D714}_{s}(t))$ and
$k(\unicode[STIX]{x1D714}_{s}(t))$ and  $k(\unicode[STIX]{x1D714}_{i}(t))$ represent the instantaneous wave vector of the pump, the signal and the idler waves, respectively. Expanding each
$k(\unicode[STIX]{x1D714}_{i}(t))$ represent the instantaneous wave vector of the pump, the signal and the idler waves, respectively. Expanding each  $k(\unicode[STIX]{x1D714}(t))$ in a Taylor series, Equation (1) can be rewritten as an approximation[Reference Witte and Eikema22]:
$k(\unicode[STIX]{x1D714}(t))$ in a Taylor series, Equation (1) can be rewritten as an approximation[Reference Witte and Eikema22]:
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x0394}k(t) & = & \displaystyle \unicode[STIX]{x0394}k_{0}+\frac{\unicode[STIX]{x2202}k_{p}(\unicode[STIX]{x1D714}_{p}(t))}{\unicode[STIX]{x2202}\unicode[STIX]{x1D714}_{p}}\unicode[STIX]{x0394}\unicode[STIX]{x1D714}_{p}-\frac{\unicode[STIX]{x2202}k_{s}(\unicode[STIX]{x1D714}_{s}(t))}{\unicode[STIX]{x2202}\unicode[STIX]{x1D714}_{s}}\unicode[STIX]{x0394}\unicode[STIX]{x1D714}_{s}\nonumber\\ \displaystyle & & \displaystyle -\,\frac{\unicode[STIX]{x2202}k_{i}(\unicode[STIX]{x1D714}_{i}(t))}{\unicode[STIX]{x2202}\unicode[STIX]{x1D714}_{i}}\unicode[STIX]{x0394}\unicode[STIX]{x1D714}_{i}+\cdots \nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x0394}k_{0}+\left(\frac{1}{\unicode[STIX]{x1D710}_{p}}-\frac{1}{\unicode[STIX]{x1D710}_{i}}\right)\unicode[STIX]{x0394}\unicode[STIX]{x1D714}_{p}\nonumber\\ \displaystyle & & \displaystyle -\,\left(\frac{1}{\unicode[STIX]{x1D710}_{s}}-\frac{1}{\unicode[STIX]{x1D710}_{i}}\right)\unicode[STIX]{x0394}\unicode[STIX]{x1D714}_{s}+\ddot{o} (\unicode[STIX]{x0394}\unicode[STIX]{x1D714}_{p},\unicode[STIX]{x0394}\unicode[STIX]{x1D714}_{s}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x0394}k(t) & = & \displaystyle \unicode[STIX]{x0394}k_{0}+\frac{\unicode[STIX]{x2202}k_{p}(\unicode[STIX]{x1D714}_{p}(t))}{\unicode[STIX]{x2202}\unicode[STIX]{x1D714}_{p}}\unicode[STIX]{x0394}\unicode[STIX]{x1D714}_{p}-\frac{\unicode[STIX]{x2202}k_{s}(\unicode[STIX]{x1D714}_{s}(t))}{\unicode[STIX]{x2202}\unicode[STIX]{x1D714}_{s}}\unicode[STIX]{x0394}\unicode[STIX]{x1D714}_{s}\nonumber\\ \displaystyle & & \displaystyle -\,\frac{\unicode[STIX]{x2202}k_{i}(\unicode[STIX]{x1D714}_{i}(t))}{\unicode[STIX]{x2202}\unicode[STIX]{x1D714}_{i}}\unicode[STIX]{x0394}\unicode[STIX]{x1D714}_{i}+\cdots \nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x0394}k_{0}+\left(\frac{1}{\unicode[STIX]{x1D710}_{p}}-\frac{1}{\unicode[STIX]{x1D710}_{i}}\right)\unicode[STIX]{x0394}\unicode[STIX]{x1D714}_{p}\nonumber\\ \displaystyle & & \displaystyle -\,\left(\frac{1}{\unicode[STIX]{x1D710}_{s}}-\frac{1}{\unicode[STIX]{x1D710}_{i}}\right)\unicode[STIX]{x0394}\unicode[STIX]{x1D714}_{s}+\ddot{o} (\unicode[STIX]{x0394}\unicode[STIX]{x1D714}_{p},\unicode[STIX]{x0394}\unicode[STIX]{x1D714}_{s}),\end{eqnarray}$$ where  $\unicode[STIX]{x1D710}=\unicode[STIX]{x2202}\unicode[STIX]{x1D714}/\unicode[STIX]{x2202}k(\unicode[STIX]{x1D714}(t))$ denotes the group velocity,
$\unicode[STIX]{x1D710}=\unicode[STIX]{x2202}\unicode[STIX]{x1D714}/\unicode[STIX]{x2202}k(\unicode[STIX]{x1D714}(t))$ denotes the group velocity,  $\unicode[STIX]{x0394}\unicode[STIX]{x1D714}=\unicode[STIX]{x1D6FC}t$ refers to the instantaneous offset angular frequency and
$\unicode[STIX]{x0394}\unicode[STIX]{x1D714}=\unicode[STIX]{x1D6FC}t$ refers to the instantaneous offset angular frequency and  $\ddot{o}$ represents the higher-order dispersion terms. The perfect PM condition is normally satisfied at the central frequencies
$\ddot{o}$ represents the higher-order dispersion terms. The perfect PM condition is normally satisfied at the central frequencies  $(\unicode[STIX]{x0394}k_{0}=0)$. Then, to realize a broadband PM environment, the wave-vector mismatch
$(\unicode[STIX]{x0394}k_{0}=0)$. Then, to realize a broadband PM environment, the wave-vector mismatch  $\unicode[STIX]{x0394}k$ may be canceled to the first order, only if the frequency shifts
$\unicode[STIX]{x0394}k$ may be canceled to the first order, only if the frequency shifts  $\unicode[STIX]{x0394}\unicode[STIX]{x1D714}_{p}$ and
$\unicode[STIX]{x0394}\unicode[STIX]{x1D714}_{p}$ and  $\unicode[STIX]{x0394}\unicode[STIX]{x1D714}_{s}$ are properly arranged as
$\unicode[STIX]{x0394}\unicode[STIX]{x1D714}_{s}$ are properly arranged as
 $$\begin{eqnarray}\frac{\unicode[STIX]{x0394}\unicode[STIX]{x1D714}_{s}}{\unicode[STIX]{x0394}\unicode[STIX]{x1D714}_{p}}=\frac{\unicode[STIX]{x1D6FC}_{s}}{\unicode[STIX]{x1D6FC}_{p}}=\frac{\displaystyle \frac{1}{\unicode[STIX]{x1D710}_{p}}-\frac{1}{\unicode[STIX]{x1D710}_{i}}}{\displaystyle \frac{1}{\unicode[STIX]{x1D710}_{s}}-\frac{1}{\unicode[STIX]{x1D710}_{i}}}=\unicode[STIX]{x1D70E},\end{eqnarray}$$
$$\begin{eqnarray}\frac{\unicode[STIX]{x0394}\unicode[STIX]{x1D714}_{s}}{\unicode[STIX]{x0394}\unicode[STIX]{x1D714}_{p}}=\frac{\unicode[STIX]{x1D6FC}_{s}}{\unicode[STIX]{x1D6FC}_{p}}=\frac{\displaystyle \frac{1}{\unicode[STIX]{x1D710}_{p}}-\frac{1}{\unicode[STIX]{x1D710}_{i}}}{\displaystyle \frac{1}{\unicode[STIX]{x1D710}_{s}}-\frac{1}{\unicode[STIX]{x1D710}_{i}}}=\unicode[STIX]{x1D70E},\end{eqnarray}$$ where  $(1/\unicode[STIX]{x1D710}_{p}-1/\unicode[STIX]{x1D710}_{i})/(1/\unicode[STIX]{x1D710}_{s}-1/\unicode[STIX]{x1D710}_{i})$ is termed the correlation coefficient of the group velocity and annotated as
$(1/\unicode[STIX]{x1D710}_{p}-1/\unicode[STIX]{x1D710}_{i})/(1/\unicode[STIX]{x1D710}_{s}-1/\unicode[STIX]{x1D710}_{i})$ is termed the correlation coefficient of the group velocity and annotated as  $\unicode[STIX]{x1D70E}$ for simplicity. For any given parametric process, we can always realize the near-ideal broadband frequency conversion by regulating the ratio of
$\unicode[STIX]{x1D70E}$ for simplicity. For any given parametric process, we can always realize the near-ideal broadband frequency conversion by regulating the ratio of  $\unicode[STIX]{x1D6FC}_{s}/\unicode[STIX]{x1D6FC}_{p}$ to the
$\unicode[STIX]{x1D6FC}_{s}/\unicode[STIX]{x1D6FC}_{p}$ to the  $\unicode[STIX]{x1D70E}$-determined value. However, to make the best of the broadband spectra of the driving pulses and obtain an initial spectrum-broadened idler pulse, opposite linear chirps (
$\unicode[STIX]{x1D70E}$-determined value. However, to make the best of the broadband spectra of the driving pulses and obtain an initial spectrum-broadened idler pulse, opposite linear chirps ( $\unicode[STIX]{x1D6FC}_{s}$,
$\unicode[STIX]{x1D6FC}_{s}$,  $\unicode[STIX]{x1D6FC}_{p}$) are essentially required. Then, for a given oppositely dual-chirped parametric process, we can only resort to the nonlinear crystals with a negative
$\unicode[STIX]{x1D6FC}_{p}$) are essentially required. Then, for a given oppositely dual-chirped parametric process, we can only resort to the nonlinear crystals with a negative  $\unicode[STIX]{x1D70E}$, considering the requirements of the spectrum-broadened idler generation and the subsequent broadband amplification. Efficient idler broadening can be thus achieved provided that the chirp parameters are correctly chosen
$\unicode[STIX]{x1D70E}$, considering the requirements of the spectrum-broadened idler generation and the subsequent broadband amplification. Efficient idler broadening can be thus achieved provided that the chirp parameters are correctly chosen  $(\unicode[STIX]{x1D6FC}_{s}/\unicode[STIX]{x1D6FC}_{p}=\unicode[STIX]{x1D70E})$.
$(\unicode[STIX]{x1D6FC}_{s}/\unicode[STIX]{x1D6FC}_{p}=\unicode[STIX]{x1D70E})$.
3 Selection of the nonlinear crystal
Generally, the group velocity and the resulting correlation coefficient of  $\unicode[STIX]{x1D70E}$ depend on the dispersion characteristics of the nonlinear material, and normally they are not controllable parameters in a phase-matched nonlinear medium. To take full advantage of this dual-chirped DFG scheme, it is necessary to employ suitable nonlinear crystal materials for different parametric processes. Assuming a well-developed
$\unicode[STIX]{x1D70E}$ depend on the dispersion characteristics of the nonlinear material, and normally they are not controllable parameters in a phase-matched nonlinear medium. To take full advantage of this dual-chirped DFG scheme, it is necessary to employ suitable nonlinear crystal materials for different parametric processes. Assuming a well-developed  ${\sim}790~\text{nm}$ Ti:sapphire ultrafast pulsed laser is employed as the pump laser, based on the published Sellmeier equations[Reference Gayer, Sacks, Galun and Arie23–Reference Vanherzeele, Bierlein and Zumsteg26], we systematically analyze the group-velocity relationship in various commonly used nonlinear crystals under different PM conditions. All possible OPA processes have been considered across an ultra-broad idler spectral region from
${\sim}790~\text{nm}$ Ti:sapphire ultrafast pulsed laser is employed as the pump laser, based on the published Sellmeier equations[Reference Gayer, Sacks, Galun and Arie23–Reference Vanherzeele, Bierlein and Zumsteg26], we systematically analyze the group-velocity relationship in various commonly used nonlinear crystals under different PM conditions. All possible OPA processes have been considered across an ultra-broad idler spectral region from  $1.6~\unicode[STIX]{x03BC}\text{m}$ to
$1.6~\unicode[STIX]{x03BC}\text{m}$ to  $6.5~\unicode[STIX]{x03BC}\text{m}$, and the resulting wavelength-dependent
$6.5~\unicode[STIX]{x03BC}\text{m}$, and the resulting wavelength-dependent  $\unicode[STIX]{x1D70E}$ is shown in Figure 2.
$\unicode[STIX]{x1D70E}$ is shown in Figure 2.
On one hand, a negative  $\unicode[STIX]{x1D70E}$ is the premise to realize efficient idler broadening of an oppositely dual-chirped parametric process. On the other hand, the absolute value of
$\unicode[STIX]{x1D70E}$ is the premise to realize efficient idler broadening of an oppositely dual-chirped parametric process. On the other hand, the absolute value of  $\unicode[STIX]{x1D70E}$ determines the optimum linear chirps
$\unicode[STIX]{x1D70E}$ determines the optimum linear chirps  $(\unicode[STIX]{x1D6FC}_{s}/\unicode[STIX]{x1D6FC}_{p})$ to satisfy the broadband amplification and, subsequently, the signal-to-pump ratio of the spectral components involved in the nonlinear processes. Evidently, the optimum idler broadening will be achieved when
$(\unicode[STIX]{x1D6FC}_{s}/\unicode[STIX]{x1D6FC}_{p})$ to satisfy the broadband amplification and, subsequently, the signal-to-pump ratio of the spectral components involved in the nonlinear processes. Evidently, the optimum idler broadening will be achieved when  $|\unicode[STIX]{x0394}\unicode[STIX]{x1D714}_{p}|$ and
$|\unicode[STIX]{x0394}\unicode[STIX]{x1D714}_{p}|$ and  $|\unicode[STIX]{x0394}\unicode[STIX]{x1D714}_{s}|$ are equivalent, and a group-velocity correlation coefficient of
$|\unicode[STIX]{x0394}\unicode[STIX]{x1D714}_{s}|$ are equivalent, and a group-velocity correlation coefficient of  ${\sim}-1$ is thus required.
${\sim}-1$ is thus required.

Figure 2. The wavelength-dependent  $(1/\unicode[STIX]{x1D710}_{p}-1/\unicode[STIX]{x1D710}_{i})/(1/\unicode[STIX]{x1D710}_{s}-1/\unicode[STIX]{x1D710}_{i})$ in various commonly used nonlinear crystals under different PM conditions. A well-developed
$(1/\unicode[STIX]{x1D710}_{p}-1/\unicode[STIX]{x1D710}_{i})/(1/\unicode[STIX]{x1D710}_{s}-1/\unicode[STIX]{x1D710}_{i})$ in various commonly used nonlinear crystals under different PM conditions. A well-developed  ${\sim}790~\text{nm}$ Ti:sapphire ultrafast pulsed laser is employed as the pump laser. The special cases where the generated idler wave is absorbable by the employed nonlinear crystal are also included (dashed lines), in consideration of its other potential applications[Reference Ma, Wang, Yuan, Xie, Xiong, Tu, Tu, Shi, Zheng and Qian27, Reference Leidinger, Fieberg, Waasem, Kühnemann, Buse and Breunig28]. The shadowed area indicates the desired values of
${\sim}790~\text{nm}$ Ti:sapphire ultrafast pulsed laser is employed as the pump laser. The special cases where the generated idler wave is absorbable by the employed nonlinear crystal are also included (dashed lines), in consideration of its other potential applications[Reference Ma, Wang, Yuan, Xie, Xiong, Tu, Tu, Shi, Zheng and Qian27, Reference Leidinger, Fieberg, Waasem, Kühnemann, Buse and Breunig28]. The shadowed area indicates the desired values of  $\unicode[STIX]{x1D70E}$, which may realize the optimum idler broadening.
$\unicode[STIX]{x1D70E}$, which may realize the optimum idler broadening.
As shown in Figure 2, although most of the bulk material crystals are capable of providing the desired negative  $\unicode[STIX]{x1D70E}$ at particular wavelengths, the available wavelengths are extremely limited, resulting in the steep
$\unicode[STIX]{x1D70E}$ at particular wavelengths, the available wavelengths are extremely limited, resulting in the steep  $\unicode[STIX]{x1D70E}$-curves in the negative area. Even when all of the mentioned nonlinear crystals are integrated, the broadband PM condition can still be realized only in discrete narrow bands for the oppositely dual-chirped DFG design. This result is consistent with the previous conclusion that opposite chirp signs normally provide more rigorous PM conditions[Reference Fu, Takahashi and Midorikawa29, Reference Yin, Li, Ren, Wang, Chew and Chang30]. To promote the application of such a DFG scheme, it is essential to explore the nonlinear materials possessing the required dispersion characteristics in a broader spectral range. Besides birefringence-based bulk crystals, PPLN is another potential candidate because of its large conversion efficiency and possibility for engineering[Reference Bigler, Pupeikis, Hrisafov, Gallmann, Phillips and Keller31–Reference Neese, Phillips, Gallmann, Fejer and Keller33]. Normally, to make use of the largest nonlinear coefficient of
$\unicode[STIX]{x1D70E}$-curves in the negative area. Even when all of the mentioned nonlinear crystals are integrated, the broadband PM condition can still be realized only in discrete narrow bands for the oppositely dual-chirped DFG design. This result is consistent with the previous conclusion that opposite chirp signs normally provide more rigorous PM conditions[Reference Fu, Takahashi and Midorikawa29, Reference Yin, Li, Ren, Wang, Chew and Chang30]. To promote the application of such a DFG scheme, it is essential to explore the nonlinear materials possessing the required dispersion characteristics in a broader spectral range. Besides birefringence-based bulk crystals, PPLN is another potential candidate because of its large conversion efficiency and possibility for engineering[Reference Bigler, Pupeikis, Hrisafov, Gallmann, Phillips and Keller31–Reference Neese, Phillips, Gallmann, Fejer and Keller33]. Normally, to make use of the largest nonlinear coefficient of  $d_{33}$, a Type-0 QPM condition (ee-e) should be satisfied. However, the inactive Type-I (oo-e) or Type-II (eo-o) QPM conditions may also have an advantage in certain broadband nonlinear processes[Reference Yu, Ro, Cha, Kurimura and Taira34, Reference Zhong, Zhang, Li and Fan35]. Compared to other material counterparts, the Type-II PPLN not only exhibits a stable group-velocity relationship across an extremely broad spectral range (1000–1600 nm), but
$d_{33}$, a Type-0 QPM condition (ee-e) should be satisfied. However, the inactive Type-I (oo-e) or Type-II (eo-o) QPM conditions may also have an advantage in certain broadband nonlinear processes[Reference Yu, Ro, Cha, Kurimura and Taira34, Reference Zhong, Zhang, Li and Fan35]. Compared to other material counterparts, the Type-II PPLN not only exhibits a stable group-velocity relationship across an extremely broad spectral range (1000–1600 nm), but  $\unicode[STIX]{x1D70E}$ also stays within relatively ideal boundary values
$\unicode[STIX]{x1D70E}$ also stays within relatively ideal boundary values  $(-1.5<\unicode[STIX]{x1D70E}<-0.5)$.
$(-1.5<\unicode[STIX]{x1D70E}<-0.5)$.
Intrinsically, oppositely dual-chirped DFG is capable of generating the conspicuously broader mid-IR pulsed seeding than the driving pulsed lasers, which is the premise of generating the high-intensity pulsed laser. However, only if the broadband PM condition is satisfied can the subsequent effective energy transfer be realized. Provided that an appropriate nonlinear crystal material is selected and the pump and signal waves are properly pre-chirped, broadband frequency conversion is achievable over an extremely broad spectral range.
Table 1. Nonlinear optical parameters for the 5% doped MgO:PPLN and the YCOB crystal at  $24.5\,^{\circ }\text{C}$ (
$24.5\,^{\circ }\text{C}$ ( $\unicode[STIX]{x1D706}_{p}=790~\text{nm}$,
$\unicode[STIX]{x1D706}_{p}=790~\text{nm}$,  $\unicode[STIX]{x1D706}_{s}=1030~\text{nm}$,
$\unicode[STIX]{x1D706}_{s}=1030~\text{nm}$,  $\unicode[STIX]{x1D706}_{i}=3.4~\unicode[STIX]{x03BC}\text{m}$).
$\unicode[STIX]{x1D706}_{i}=3.4~\unicode[STIX]{x03BC}\text{m}$).

4 Gain characteristics of the Type-II PPLN crystal
According to the crystal-selection strategy presented in the previous section, the Type-II PPLN crystal shows an attractive application to generate high-intensity pulsed laser at  $2.0{-}4.0~\unicode[STIX]{x03BC}\text{m}$. In what follows, we discussed in detail a typical mid-IR parametric process to exploit the gain-spectrum characteristics of such a broadband phase-matched oppositely dual-chirped difference frequency generator.
$2.0{-}4.0~\unicode[STIX]{x03BC}\text{m}$. In what follows, we discussed in detail a typical mid-IR parametric process to exploit the gain-spectrum characteristics of such a broadband phase-matched oppositely dual-chirped difference frequency generator.
We take a conventional 790 nm Ti:sapphire pulsed laser as the pump laser, for which  $I(t)=I_{0}\cdot \exp [-2(t/\unicode[STIX]{x1D70F}_{0})^{2}]$.
$I(t)=I_{0}\cdot \exp [-2(t/\unicode[STIX]{x1D70F}_{0})^{2}]$.  $I_{0}=nc\unicode[STIX]{x1D700}_{0}E_{0}^{2}/2$ represents the peak intensity, and
$I_{0}=nc\unicode[STIX]{x1D700}_{0}E_{0}^{2}/2$ represents the peak intensity, and  $\unicode[STIX]{x1D70F}_{0}$ is the pulse duration in half-width at
$\unicode[STIX]{x1D70F}_{0}$ is the pulse duration in half-width at  $1/e^{2}$ maximum of the radial intensity distribution. The white-light continuum generated by part of the pump laser serves as the signal. In our simulations, an initial
$1/e^{2}$ maximum of the radial intensity distribution. The white-light continuum generated by part of the pump laser serves as the signal. In our simulations, an initial  ${\sim}120~\text{fs}$ (FWHM) Gaussian pump laser at 790 nm (i.e.,
${\sim}120~\text{fs}$ (FWHM) Gaussian pump laser at 790 nm (i.e.,  $\unicode[STIX]{x1D70F}_{0}=100~\text{fs}$) is temporally stretched to
$\unicode[STIX]{x1D70F}_{0}=100~\text{fs}$) is temporally stretched to  ${\sim}60~\text{ps}$ for 500 times, corresponding to a linear chirp coefficient
${\sim}60~\text{ps}$ for 500 times, corresponding to a linear chirp coefficient  $\unicode[STIX]{x1D6FC}_{p}$ of
$\unicode[STIX]{x1D6FC}_{p}$ of  ${\sim}0.06~\text{THz}/\text{ps}$. The linear chirp of the signal
${\sim}0.06~\text{THz}/\text{ps}$. The linear chirp of the signal  $(\unicode[STIX]{x1D6FC}_{s})$ can be adjusted to obtain different
$(\unicode[STIX]{x1D6FC}_{s})$ can be adjusted to obtain different  $\unicode[STIX]{x1D6FC}_{s}/\unicode[STIX]{x1D6FC}_{p}$ and various instantaneous frequency pairs. The signal laser centers at 1030 nm, having a flat-top and sufficiently broad spectral profile. This assumption may reduce the influence of the pulse shape on the efficiency and, therefore, on the generated idler spectrum. Accordingly, the mid-IR chirped pulsed laser at
$\unicode[STIX]{x1D6FC}_{s}/\unicode[STIX]{x1D6FC}_{p}$ and various instantaneous frequency pairs. The signal laser centers at 1030 nm, having a flat-top and sufficiently broad spectral profile. This assumption may reduce the influence of the pulse shape on the efficiency and, therefore, on the generated idler spectrum. Accordingly, the mid-IR chirped pulsed laser at  ${\sim}3.4~\unicode[STIX]{x03BC}\text{m}$ can be generated.
${\sim}3.4~\unicode[STIX]{x03BC}\text{m}$ can be generated.

Figure 3. (a), (b) The calculated conversion efficiency and idler spectral bandwidth versus the ratio of  $\unicode[STIX]{x1D6FC}_{s}/\unicode[STIX]{x1D6FC}_{p}$ in a weak-conversion situation
$\unicode[STIX]{x1D6FC}_{s}/\unicode[STIX]{x1D6FC}_{p}$ in a weak-conversion situation  $(L=5~\text{mm})$. (c), (d) The gain in the spectrum is introduced to evaluate the performance of such a difference frequency generator as the spectrum broader.
$(L=5~\text{mm})$. (c), (d) The gain in the spectrum is introduced to evaluate the performance of such a difference frequency generator as the spectrum broader.
The conversion efficiency and the idler spectral bandwidth versus the ratio of  $\unicode[STIX]{x1D6FC}_{s}/\unicode[STIX]{x1D6FC}_{p}$ in a weak-conversion situation are presented in Figure 3(a). The simulated parametric processes are numerically implemented based on the well-developed nonlinear coupled-wave equations under a plane wave approximation[Reference Li, Zhong, Yang, Wang and Fan36]. A 5-mm Type-II PPLN is chosen as the nonlinear medium and the initial signal intensity is fixed at 1% of the pump intensity. The other essential crystal parameters, calculated based on the published Sellmeier equations, are listed in Table 1[Reference Gayer, Sacks, Galun and Arie23, Reference Segonds, Boulanger, Fève, Ménaert, Zaccaro, Aka and Pelenc24]. In our simulations, dispersion terms of the GVM and the group-velocity dispersion (GVD) were both considered.
$\unicode[STIX]{x1D6FC}_{s}/\unicode[STIX]{x1D6FC}_{p}$ in a weak-conversion situation are presented in Figure 3(a). The simulated parametric processes are numerically implemented based on the well-developed nonlinear coupled-wave equations under a plane wave approximation[Reference Li, Zhong, Yang, Wang and Fan36]. A 5-mm Type-II PPLN is chosen as the nonlinear medium and the initial signal intensity is fixed at 1% of the pump intensity. The other essential crystal parameters, calculated based on the published Sellmeier equations, are listed in Table 1[Reference Gayer, Sacks, Galun and Arie23, Reference Segonds, Boulanger, Fève, Ménaert, Zaccaro, Aka and Pelenc24]. In our simulations, dispersion terms of the GVM and the group-velocity dispersion (GVD) were both considered.
Both the obtained idler spectrum and the conversion efficiency exhibit similar trends as a function of the ratio of  $\unicode[STIX]{x1D6FC}_{s}/\unicode[STIX]{x1D6FC}_{p}$ and achieve the maximum when the
$\unicode[STIX]{x1D6FC}_{s}/\unicode[STIX]{x1D6FC}_{p}$ and achieve the maximum when the  $\unicode[STIX]{x1D6FC}_{s}/\unicode[STIX]{x1D6FC}_{p}$ is
$\unicode[STIX]{x1D6FC}_{s}/\unicode[STIX]{x1D6FC}_{p}$ is  $-0.75$ (
$-0.75$ ( ${\sim}190~\text{nm}$) and
${\sim}190~\text{nm}$) and  $-0.65$ (
$-0.65$ ( ${\sim}2.9\%$), respectively. As shown in Figure 2, the
${\sim}2.9\%$), respectively. As shown in Figure 2, the  $\unicode[STIX]{x1D70E}$ of the Type-II PPLN crystal is
$\unicode[STIX]{x1D70E}$ of the Type-II PPLN crystal is  ${\sim}-0.65$ for such a DFG process. Therefore, the ideal broadband PM and the maximum conversion efficiency should be realized when
${\sim}-0.65$ for such a DFG process. Therefore, the ideal broadband PM and the maximum conversion efficiency should be realized when  $\unicode[STIX]{x1D6FC}_{s}/\unicode[STIX]{x1D6FC}_{p}$ is
$\unicode[STIX]{x1D6FC}_{s}/\unicode[STIX]{x1D6FC}_{p}$ is  ${\sim}-0.65$, which is in good agreement with the simulation results. By comparison, the development of the idler spectrum acts slightly differently. It should be noted that there are two primary elements determining the bandwidth of the obtained idler wave, the initial idler spectrum and the bandwidth of the parametric process. Since the 790-nm-chirped pump wave is constant, an increase in
${\sim}-0.65$, which is in good agreement with the simulation results. By comparison, the development of the idler spectrum acts slightly differently. It should be noted that there are two primary elements determining the bandwidth of the obtained idler wave, the initial idler spectrum and the bandwidth of the parametric process. Since the 790-nm-chirped pump wave is constant, an increase in  $|\unicode[STIX]{x1D6FC}_{s}/\unicode[STIX]{x1D6FC}_{p}|$ will cause more spectral components of the signal wave to participate in the nonlinear process, resulting in a broader idler seeding. Simultaneously, the ratio of
$|\unicode[STIX]{x1D6FC}_{s}/\unicode[STIX]{x1D6FC}_{p}|$ will cause more spectral components of the signal wave to participate in the nonlinear process, resulting in a broader idler seeding. Simultaneously, the ratio of  $\unicode[STIX]{x1D6FC}_{s}/\unicode[STIX]{x1D6FC}_{p}$ may also approximate the optimum
$\unicode[STIX]{x1D6FC}_{s}/\unicode[STIX]{x1D6FC}_{p}$ may also approximate the optimum  $\unicode[STIX]{x1D70E}$. Consequently, the bandwidth of the amplified idler wave experiences a prominent monotonical increase at first until
$\unicode[STIX]{x1D70E}$. Consequently, the bandwidth of the amplified idler wave experiences a prominent monotonical increase at first until  $\unicode[STIX]{x1D6FC}_{s}/\unicode[STIX]{x1D6FC}_{p}=-0.65$. Then, gain narrowing appears along with a decrease in the conversion efficiency. Although it may also restrict the obtained idler spectrum, the spectral bandwidth may still get an inertial enhancement thanks to a broader idler seeding when the influence of gain narrowing contributes less. However, the more significant gain-narrowing effect will eventually overcome the positive factor, resulting in a decreasing idler bandwidth with an increase in
$\unicode[STIX]{x1D6FC}_{s}/\unicode[STIX]{x1D6FC}_{p}=-0.65$. Then, gain narrowing appears along with a decrease in the conversion efficiency. Although it may also restrict the obtained idler spectrum, the spectral bandwidth may still get an inertial enhancement thanks to a broader idler seeding when the influence of gain narrowing contributes less. However, the more significant gain-narrowing effect will eventually overcome the positive factor, resulting in a decreasing idler bandwidth with an increase in  $|\unicode[STIX]{x1D6FC}_{s}/\unicode[STIX]{x1D6FC}_{p}|$.
$|\unicode[STIX]{x1D6FC}_{s}/\unicode[STIX]{x1D6FC}_{p}|$.
Further, we chose another nonlinear crystal with a positive group-velocity coefficient  $\unicode[STIX]{x1D70E}$ to illustrate the decisive impact of broadband PM on the oppositely dual-chirped DFG scheme. As shown in Figure 2, an yttrium calcium oxyborate (YCOB) crystal that satisfies a Type-I PM condition in the
$\unicode[STIX]{x1D70E}$ to illustrate the decisive impact of broadband PM on the oppositely dual-chirped DFG scheme. As shown in Figure 2, an yttrium calcium oxyborate (YCOB) crystal that satisfies a Type-I PM condition in the  $xz$ plane offers a positive
$xz$ plane offers a positive  $\unicode[STIX]{x1D70E}$ of
$\unicode[STIX]{x1D70E}$ of  ${\sim}1.3$ for the same parametric process. The
${\sim}1.3$ for the same parametric process. The  $\unicode[STIX]{x1D6FC}_{s}/\unicode[STIX]{x1D6FC}_{p}$-dependent conversion efficiency and idler spectral bandwidth are comparatively presented in Figure 3(b). Similarly, the crystal length is set to 5 mm, and the pump intensity is fixed at
$\unicode[STIX]{x1D6FC}_{s}/\unicode[STIX]{x1D6FC}_{p}$-dependent conversion efficiency and idler spectral bandwidth are comparatively presented in Figure 3(b). Similarly, the crystal length is set to 5 mm, and the pump intensity is fixed at  ${\sim}3.3~\text{GW}/\text{cm}^{2}$ to sustain a comparable nonlinear length
${\sim}3.3~\text{GW}/\text{cm}^{2}$ to sustain a comparable nonlinear length  $L_{nl}$, which measures the parametric gain and determines the available conversion efficiency in a perfect PM situation[Reference Petrov and Noack37]. Unlike the Type-II PPLN crystal, YCOB is incapable of satisfying the broadband PM condition when the pump and the signal waves are oppositely expanded. As a result, the conversion efficiency can only monotonously decrease with an increase in
$L_{nl}$, which measures the parametric gain and determines the available conversion efficiency in a perfect PM situation[Reference Petrov and Noack37]. Unlike the Type-II PPLN crystal, YCOB is incapable of satisfying the broadband PM condition when the pump and the signal waves are oppositely expanded. As a result, the conversion efficiency can only monotonously decrease with an increase in  $|\unicode[STIX]{x1D6FC}_{s}/\unicode[STIX]{x1D6FC}_{p}|$. The idler spectrum, meanwhile, may keep moderately broadening owing to more spectral components (signal) participating in this parameter process.
$|\unicode[STIX]{x1D6FC}_{s}/\unicode[STIX]{x1D6FC}_{p}|$. The idler spectrum, meanwhile, may keep moderately broadening owing to more spectral components (signal) participating in this parameter process.
In conclusion, the oppositely dual-chirped DFG scheme may provide the simultaneous achievement of higher conversion efficiency, broadened idler spectrum and potentially shorter pulse duration after compression if the broadband PM condition is satisfied.
5 Tunable mid-IR spectrum broader
When the constant chirped pump wave is utilized, a broader signal wave is advantageous to the generation of a broader idler wave. To evaluate the performance of such a difference frequency generator as the spectrum broader, we introduce the gain in spectrum, defined as the ratio between the bandwidth of the obtained idler wave  $(\unicode[STIX]{x0394}\unicode[STIX]{x1D714}_{i})$ and the greater between the initialized pump
$(\unicode[STIX]{x0394}\unicode[STIX]{x1D714}_{i})$ and the greater between the initialized pump  $(\unicode[STIX]{x0394}\unicode[STIX]{x1D714}_{p0})$ and signal waves
$(\unicode[STIX]{x0394}\unicode[STIX]{x1D714}_{p0})$ and signal waves  $(\unicode[STIX]{x0394}\unicode[STIX]{x1D714}_{s0}=\unicode[STIX]{x1D6FC}_{s}/\unicode[STIX]{x1D6FC}_{p}\cdot \unicode[STIX]{x0394}\unicode[STIX]{x1D714}_{p0})$[Reference Osvay and Ross38]. As shown in Figure 3(c), for the Type-II PPLN crystal, the spectrum gain reaches a maximum of
$(\unicode[STIX]{x0394}\unicode[STIX]{x1D714}_{s0}=\unicode[STIX]{x1D6FC}_{s}/\unicode[STIX]{x1D6FC}_{p}\cdot \unicode[STIX]{x0394}\unicode[STIX]{x1D714}_{p0})$[Reference Osvay and Ross38]. As shown in Figure 3(c), for the Type-II PPLN crystal, the spectrum gain reaches a maximum of  ${\sim}1.4$ in a near optimum broadband PM situation
${\sim}1.4$ in a near optimum broadband PM situation  $(\unicode[STIX]{x1D6FC}_{s}/\unicode[STIX]{x1D6FC}_{p}=-0.75)$. Although another type of spectrum narrowing is present owing to the nonuniform Gaussian envelope of the pump wave, an effective spectrum broadening can still be achieved. In theory, the ideal value should be
$(\unicode[STIX]{x1D6FC}_{s}/\unicode[STIX]{x1D6FC}_{p}=-0.75)$. Although another type of spectrum narrowing is present owing to the nonuniform Gaussian envelope of the pump wave, an effective spectrum broadening can still be achieved. In theory, the ideal value should be  ${\sim}1.75$ when both spectrum-narrowing effects are absent; i.e.,
${\sim}1.75$ when both spectrum-narrowing effects are absent; i.e.,  $(\unicode[STIX]{x0394}\unicode[STIX]{x1D714}_{p0}+\unicode[STIX]{x0394}\unicode[STIX]{x1D714}_{s0})/\text{Max}(\unicode[STIX]{x0394}\unicode[STIX]{x1D714}_{p0},\unicode[STIX]{x0394}\unicode[STIX]{x1D714}_{s0})$. Contrarily, the maximum spectrum gain of the YCOB crystal is only
$(\unicode[STIX]{x0394}\unicode[STIX]{x1D714}_{p0}+\unicode[STIX]{x0394}\unicode[STIX]{x1D714}_{s0})/\text{Max}(\unicode[STIX]{x0394}\unicode[STIX]{x1D714}_{p0},\unicode[STIX]{x0394}\unicode[STIX]{x1D714}_{s0})$. Contrarily, the maximum spectrum gain of the YCOB crystal is only  ${\sim}0.3$.
${\sim}0.3$.
Note that  $\unicode[STIX]{x0394}\unicode[STIX]{x1D714}_{i}$ may approximately scale with the incident spectral bandwidths when the optimum broadband PM condition is satisfied, and the gain in the spectrum will be nearly independent on the length of the crystal. However, for the non-optimized parametric processes, the achievable
$\unicode[STIX]{x0394}\unicode[STIX]{x1D714}_{i}$ may approximately scale with the incident spectral bandwidths when the optimum broadband PM condition is satisfied, and the gain in the spectrum will be nearly independent on the length of the crystal. However, for the non-optimized parametric processes, the achievable  $\unicode[STIX]{x0394}\unicode[STIX]{x1D714}_{i}$ may also depend on the gain-narrowing effect and the crystal length, and the optimum spectrum gain can be obtained only using an infinitely thin crystal (shown in Figures 3(c) and 3(d)).
$\unicode[STIX]{x0394}\unicode[STIX]{x1D714}_{i}$ may also depend on the gain-narrowing effect and the crystal length, and the optimum spectrum gain can be obtained only using an infinitely thin crystal (shown in Figures 3(c) and 3(d)).
As a conclusion, the broadband phase-matched oppositely dual-chirped DFG shows an extraordinary ability to make the most of the pump energy and spectral components of the interacting pump and signal waves achieve efficient idler broadening. However, the initial linear chirps  $(\unicode[STIX]{x1D6FC}_{s}/\unicode[STIX]{x1D6FC}_{p})$ have to be specifically optimized for various given parametric processes and nonlinear media.
$(\unicode[STIX]{x1D6FC}_{s}/\unicode[STIX]{x1D6FC}_{p})$ have to be specifically optimized for various given parametric processes and nonlinear media.

Figure 4. Schematic of a tunable mid-IR spectrum broader based on the oppositely dual-chirped DFG scheme. BS, beam splitter; DM, dichroic mirror; DL, delay line;  $\text{L}_{1}$ and
$\text{L}_{1}$ and  $\text{L}_{2}$, lenses; C, sapphire plate.
$\text{L}_{2}$, lenses; C, sapphire plate.
As shown in Figure 2, when a conventional Ti:sapphire pump laser at 790 nm is employed, the Type-II PPLN crystal is capable of providing the required negative  $\unicode[STIX]{x1D70E}$ across an extremely broad spectral range from
$\unicode[STIX]{x1D70E}$ across an extremely broad spectral range from  ${\sim}1000~\text{nm}$ to
${\sim}1000~\text{nm}$ to  ${\sim}1600~\text{nm}$ (
${\sim}1600~\text{nm}$ ( $-1.5<\unicode[STIX]{x1D70E}<-0.5$) to fulfill the oppositely dual-chirped broadband frequency conversion. In view of its unique superiority in such a DFG configuration, the Type-II PPLN can be potentially used to construct a tunable mid-IR spectrum broader. As shown in Figure 4, a 790 nm Ti:sapphire pulsed laser is employed as the driving laser. A fraction of the driving laser is diverted by the beam splitter for continuum generation. Then, the generated white-light continuum and the majority of the pump laser are respectively directed to separate pulse stretchers (e.g., the chirped mirrors and the prism pairs) and converted to chirped pulses with opposite chirp signs. The pump laser is combined with the white-light continuum after passing through a path-length-matching optical delay line. Finally, the collinear pulses are overlapped in the Type-II PPLN crystal with a specified fan-out grating design[Reference Sukeert, Kumar and Ebrahim-Zadeh39]. To realize the QPM for various signal wavelengths from
$-1.5<\unicode[STIX]{x1D70E}<-0.5$) to fulfill the oppositely dual-chirped broadband frequency conversion. In view of its unique superiority in such a DFG configuration, the Type-II PPLN can be potentially used to construct a tunable mid-IR spectrum broader. As shown in Figure 4, a 790 nm Ti:sapphire pulsed laser is employed as the driving laser. A fraction of the driving laser is diverted by the beam splitter for continuum generation. Then, the generated white-light continuum and the majority of the pump laser are respectively directed to separate pulse stretchers (e.g., the chirped mirrors and the prism pairs) and converted to chirped pulses with opposite chirp signs. The pump laser is combined with the white-light continuum after passing through a path-length-matching optical delay line. Finally, the collinear pulses are overlapped in the Type-II PPLN crystal with a specified fan-out grating design[Reference Sukeert, Kumar and Ebrahim-Zadeh39]. To realize the QPM for various signal wavelengths from  ${\sim}980~\text{nm}$ to
${\sim}980~\text{nm}$ to  ${\sim}1500~\text{nm}$, the Type-II PPLN crystal should be properly designed with continuous grating periods from
${\sim}1500~\text{nm}$, the Type-II PPLN crystal should be properly designed with continuous grating periods from  $7.2~\unicode[STIX]{x03BC}\text{m}$ to
$7.2~\unicode[STIX]{x03BC}\text{m}$ to  $9.1~\unicode[STIX]{x03BC}\text{m}$. In response, a tunable mid-IR idler wave from
$9.1~\unicode[STIX]{x03BC}\text{m}$. In response, a tunable mid-IR idler wave from  ${\sim}1.7~\unicode[STIX]{x03BC}\text{m}$ to
${\sim}1.7~\unicode[STIX]{x03BC}\text{m}$ to  ${\sim}4.0~\unicode[STIX]{x03BC}\text{m}$ can be obtained after the pulse compression. Wavelength-tuning of the mid-IR spectrum broader is accomplished mainly by synchronizing the chirped pump pulse to various instantaneous frequency components of the strongly chirp-stretched white-light continuum through the adjustment of the optical delay[Reference Reed, Steiner-Shepard and Negus40, Reference Shirakawa and Kobayashi41]. Grating period
${\sim}4.0~\unicode[STIX]{x03BC}\text{m}$ can be obtained after the pulse compression. Wavelength-tuning of the mid-IR spectrum broader is accomplished mainly by synchronizing the chirped pump pulse to various instantaneous frequency components of the strongly chirp-stretched white-light continuum through the adjustment of the optical delay[Reference Reed, Steiner-Shepard and Negus40, Reference Shirakawa and Kobayashi41]. Grating period  $\unicode[STIX]{x1D6EC}$ of the Type-II PPLN should be simultaneously regulated for phase-matching. Thanks to the negative and relatively constant correlation coefficient
$\unicode[STIX]{x1D6EC}$ of the Type-II PPLN should be simultaneously regulated for phase-matching. Thanks to the negative and relatively constant correlation coefficient  $\unicode[STIX]{x1D70E}$ of the Type-II PPLN crystal, the presented DFG configuration removes the complex operation of drastically adjusting the ratio of
$\unicode[STIX]{x1D70E}$ of the Type-II PPLN crystal, the presented DFG configuration removes the complex operation of drastically adjusting the ratio of  $\unicode[STIX]{x1D6FC}_{s}/\unicode[STIX]{x1D6FC}_{p}$ for various signal wavelengths. Only a slight adjustment of the chirp parameter of the pump or the signal wave is required to optimize the results.
$\unicode[STIX]{x1D6FC}_{s}/\unicode[STIX]{x1D6FC}_{p}$ for various signal wavelengths. Only a slight adjustment of the chirp parameter of the pump or the signal wave is required to optimize the results.

Figure 5. The calculated conversion efficiency and TL pulse duration of the generated idler wave as a function of the signal wavelength, which is continuously tuned from 980 nm to 1100 nm and from 1100 nm to 1500 nm, respectively. Note that, the TL pulse duration of the initialized 790 nm pump laser is  ${\sim}120~\text{fs}$. Solid line, a Type-II PPLN crystal is employed and the
${\sim}120~\text{fs}$. Solid line, a Type-II PPLN crystal is employed and the  $\unicode[STIX]{x1D6FC}_{s}/\unicode[STIX]{x1D6FC}_{p}$ is optimized for various signal wavelengths; dashed line, the ideal cases, where the material dispersions are absent; dotted line, the comparison results based on a conventional Type-0 PPLN crystal. (a)
$\unicode[STIX]{x1D6FC}_{s}/\unicode[STIX]{x1D6FC}_{p}$ is optimized for various signal wavelengths; dashed line, the ideal cases, where the material dispersions are absent; dotted line, the comparison results based on a conventional Type-0 PPLN crystal. (a)  $I_{p}=0.4~\text{GW}/\text{cm}^{2}$; (b)
$I_{p}=0.4~\text{GW}/\text{cm}^{2}$; (b)  $I_{p}=0.25~\text{GW}/\text{cm}^{2}$; (c)
$I_{p}=0.25~\text{GW}/\text{cm}^{2}$; (c)  $I_{p}=1.2~\text{GW}/\text{cm}^{2}$; (d)
$I_{p}=1.2~\text{GW}/\text{cm}^{2}$; (d)  $I_{p}=0.8~\text{GW}/\text{cm}^{2}$.
$I_{p}=0.8~\text{GW}/\text{cm}^{2}$.
Assuming a 10 mm Type-II PPLN crystal is employed, the initial  ${\sim}120~\text{fs}$ (FWHM) Gaussian pump laser at 790 nm is temporally stretched to
${\sim}120~\text{fs}$ (FWHM) Gaussian pump laser at 790 nm is temporally stretched to  ${\sim}120~\text{ps}$ for 1000 times. The continuum seeding has a flat-top and sufficiently broad spectral profile. The initial signal intensity is fixed at 1% of the pump intensity.
${\sim}120~\text{ps}$ for 1000 times. The continuum seeding has a flat-top and sufficiently broad spectral profile. The initial signal intensity is fixed at 1% of the pump intensity.  $\unicode[STIX]{x1D6FC}_{s}/\unicode[STIX]{x1D6FC}_{p}$ is always optimized for various signal wavelengths, so that the broadband PM condition is achieved.
$\unicode[STIX]{x1D6FC}_{s}/\unicode[STIX]{x1D6FC}_{p}$ is always optimized for various signal wavelengths, so that the broadband PM condition is achieved.
Figures 5(a) and 5(b) present the small-signal conversion efficiency and the TL pulse duration of the generated idler wave when the signal wavelength is continuously tuned from 980 nm to 1100 nm and from 1100 nm to 1500 nm, respectively. The TL pulse duration is derived from the calculated idler spectrum supposing the obtained idler wave is well compressed. The broadband phase-matched oppositely dual-chirped DFG scheme exhibits an expected performance close to the ideal case that the material dispersions are absent. That moderate discrepancy may be ascribed to the un-compensated second- and higher-order terms of  $\unicode[STIX]{x0394}k$. The comparison result based on a conventional Type-0 PPLN crystal is also presented under a same operation environment. In consideration of its 5.5 times larger
$\unicode[STIX]{x0394}k$. The comparison result based on a conventional Type-0 PPLN crystal is also presented under a same operation environment. In consideration of its 5.5 times larger  $d_{\text{eff}}$, a significantly shorter crystal of
$d_{\text{eff}}$, a significantly shorter crystal of  ${\sim}1.8~\text{mm}$ is chosen to ensure that a comparable dispersion-absent performance to the 10 mm Type-II PPLN crystal can be achieved. It is predicted that the Type-II PPLN crystal may nearly always lead to a shorter TL pulse duration and higher conversion efficiency compared with its counterpart. Figures 5(c) and 5(d) present the results when the pump intensity is respectively elevated to
${\sim}1.8~\text{mm}$ is chosen to ensure that a comparable dispersion-absent performance to the 10 mm Type-II PPLN crystal can be achieved. It is predicted that the Type-II PPLN crystal may nearly always lead to a shorter TL pulse duration and higher conversion efficiency compared with its counterpart. Figures 5(c) and 5(d) present the results when the pump intensity is respectively elevated to  ${\sim}1.2~\text{GW}/\text{cm}^{2}$ and
${\sim}1.2~\text{GW}/\text{cm}^{2}$ and  ${\sim}0.8~\text{GW}/\text{cm}^{2}$. Since the pump and the signal waves are both sufficiently temporally chirped, the instantaneous parametric processes between various frequency pairs proceed nearly independently. The conversion efficiency and the TL pulse duration present similar tuning characteristics to those of the small-signal cases.
${\sim}0.8~\text{GW}/\text{cm}^{2}$. Since the pump and the signal waves are both sufficiently temporally chirped, the instantaneous parametric processes between various frequency pairs proceed nearly independently. The conversion efficiency and the TL pulse duration present similar tuning characteristics to those of the small-signal cases.
6 Conclusion
Oppositely dual-chirped DFG is advantageous for obtaining a spectrum-broadened idler seeding compared with the incident pump and signal waves. However, the normally more rigorous broadband PM condition hampers its application in the generation of an ultrafast mid-IR pulsed laser. In association with the fundamental PM equations and the chirp characteristics of such DFG schemes, we derived the intrinsic requirement of the broadband frequency conversion on both the group-velocity correlation and the chirp parameters, and used this as a strategy to choose the appropriate nonlinear crystals for various parametric processes. Although most of the birefringence bulk crystals can only provide the required material dispersions in extremely limited spectral regions, the PPLN crystal that satisfies an inactive Type-II (eo-o) QPM condition has a relatively stable negative  $\unicode[STIX]{x1D70E}$ and exhibits the expected broadband gain characteristics. Finally, we proposed and numerically verified a promising DFG configuration to construct a tunable mid-IR spectrum broader based on an oppositely dual-chirped DFG scheme. It exhibits consistent and satisfactory efficiency across an ultra-broad idler spectral region
$\unicode[STIX]{x1D70E}$ and exhibits the expected broadband gain characteristics. Finally, we proposed and numerically verified a promising DFG configuration to construct a tunable mid-IR spectrum broader based on an oppositely dual-chirped DFG scheme. It exhibits consistent and satisfactory efficiency across an ultra-broad idler spectral region  $(1.7{-}4.0~\unicode[STIX]{x03BC}\text{m})$. Furthermore, efficient idler broadening is observed comparable to the ideal cases, where the material dispersions are absent. The broadband phase-matched oppositely dual-chirped difference frequency generation may serve as a promising approach for the development of high-intensity mid-IR pulsed lasers.
$(1.7{-}4.0~\unicode[STIX]{x03BC}\text{m})$. Furthermore, efficient idler broadening is observed comparable to the ideal cases, where the material dispersions are absent. The broadband phase-matched oppositely dual-chirped difference frequency generation may serve as a promising approach for the development of high-intensity mid-IR pulsed lasers.
Acknowledgements
This work was supported in part by the National Natural Science Foundation of China (No. 61505113), Natural Science Foundation of Guangdong Province (No. 2020A1515010541) and Science and Technology Project of Shenzhen (Nos. JCYJ20180305124930169, JCYJ20190808143419622 and ZDSYS201707271014468).