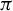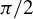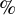1 Introduction
With the rapid development of laser technologies, a laser pulse with intensity far exceeding
![]() ${10}^{18}\ \mathrm{W}/{\mathrm{cm}}^2$
is available in laboratories[
Reference Mourou, Tajima and Bulanov
1
,
Reference Danson, Haefner, Bromage, Butcher, Chanteloup, Chowdhury, Galvanauskas, Gizzi, Hein, Hillier, Hopps, Kato, Khazanov, Kodama, Korn, Li, Li, Limpert, Ma, Nam, Neely, Papadopoulos, Penman, Qian, Rocca, Shaykin, Siders, Spindloe, Szatmári, Trines, Zhu, Zhu and Zuegel
2
]. Under the irradiation of this ultraintense laser, almost all materials are ionized into plasma and liberated electrons can rapidly oscillate in laser fields at velocities approaching the speed of light[
Reference Mourou, Tajima and Bulanov
1
]. Plasma, as an ionized product of matter, is a unique candidate for manipulating ultraintense laser pulses. Recently, numerous innovative concepts for plasma-based optical methods and devices have been proposed, including stimulated Raman and Brillouin amplification[
Reference Chiaramello, Amiranoff, Riconda and Weber
3
–
Reference Andréas, Mickael, István and Caterina
5
], plasma mirrors[
Reference Lamač, Mima, Nejdl, Chaulagain and Bulanov
6
], plasma frequency converters[
Reference Wang and Wang
7
], plasma gratings[
Reference Edwards, Waczynski, Rockafellow, Manzo, Zingale, Michel and Milchberg
8
,
Reference Li, Zou, Zeng, Wu, Wang, Wang, Mu and Hu
9
] and plasma holography[
Reference Hans, Pau and David
10
]. The transition from the conceptual stage to the realization of optical elements requires a profound comprehension of the nonlinear interaction between relativistic lasers and plasmas. To extend more application scenarios, advanced relativistic laser manipulation methods based on plasma optics are still desired.
${10}^{18}\ \mathrm{W}/{\mathrm{cm}}^2$
is available in laboratories[
Reference Mourou, Tajima and Bulanov
1
,
Reference Danson, Haefner, Bromage, Butcher, Chanteloup, Chowdhury, Galvanauskas, Gizzi, Hein, Hillier, Hopps, Kato, Khazanov, Kodama, Korn, Li, Li, Limpert, Ma, Nam, Neely, Papadopoulos, Penman, Qian, Rocca, Shaykin, Siders, Spindloe, Szatmári, Trines, Zhu, Zhu and Zuegel
2
]. Under the irradiation of this ultraintense laser, almost all materials are ionized into plasma and liberated electrons can rapidly oscillate in laser fields at velocities approaching the speed of light[
Reference Mourou, Tajima and Bulanov
1
]. Plasma, as an ionized product of matter, is a unique candidate for manipulating ultraintense laser pulses. Recently, numerous innovative concepts for plasma-based optical methods and devices have been proposed, including stimulated Raman and Brillouin amplification[
Reference Chiaramello, Amiranoff, Riconda and Weber
3
–
Reference Andréas, Mickael, István and Caterina
5
], plasma mirrors[
Reference Lamač, Mima, Nejdl, Chaulagain and Bulanov
6
], plasma frequency converters[
Reference Wang and Wang
7
], plasma gratings[
Reference Edwards, Waczynski, Rockafellow, Manzo, Zingale, Michel and Milchberg
8
,
Reference Li, Zou, Zeng, Wu, Wang, Wang, Mu and Hu
9
] and plasma holography[
Reference Hans, Pau and David
10
]. The transition from the conceptual stage to the realization of optical elements requires a profound comprehension of the nonlinear interaction between relativistic lasers and plasmas. To extend more application scenarios, advanced relativistic laser manipulation methods based on plasma optics are still desired.
In the relativistic regime, relativistic electron mass correction and plasma density redistribution induced by the ponderomotive force of the laser are responsible for nonlinear effects such as relativistic self-focusing and self-modulating instability[ Reference Ren, Hemker, Fonseca, Duda and Mori 11 , Reference Wu, Sheng and Zhang 12 ]. Both of these phenomena lead to longitudinal and transverse redistribution of laser energy, which in turn has a significant impact on charged particle acceleration, ultra-bright radiation and light amplification. When two laser beamlets copropagate in underdense plasma, more exotic effects may occur. The mutual interaction feature is characterized by attraction, repulsion and spiral due to the difference of electron dynamic behavior in different laser–plasma parameters[ Reference Ren, Hemker, Fonseca, Duda and Mori 11 – Reference Nakatsutsumi, Marquès, Antici, Bourgeois, Feugeas, Lin, Ph. Nicolaï, Kodama, Audebert and Fuchs 21 ]. In particular, even a small initial phase difference can result in a strong energy transfer between beams, which will greatly affect the formation of coupled light[ Reference Sun, Edward, Lee and Parvez 13 – Reference Dong, Sheng and Zhang 16 ]. This offers possibilities of merging multiple laser beams into a single, more powerful laser pulse.
In this paper, we propose to manipulate the energy mergence of two femtosecond (fs) seed lasers in underdense plasma by using two obliquely incident external guiding lights. It is found that the peak intensity of the merged laser is more than five times higher than that of the seed laser when the guiding laser is
![]() $\pi$
or
$\pi$
or
![]() $\pi /2$
ahead of the in-phase seed laser and incident at a small angle. The energy conversion efficiency from all incident lasers to merged light is approximately 60
$\pi /2$
ahead of the in-phase seed laser and incident at a small angle. The energy conversion efficiency from all incident lasers to merged light is approximately 60
![]() $\%$
higher. The amplification effect of the seed laser intensity is remarkable, and the mergence length is tunable in a wide laser–plasma parameter range. This might provide a feasible routine to manipulate the propagation of multiple relativistic laser pulses for applications such as plasma optics[
Reference Myatt, Pesme, Hüller, Maximov, Rozmus and Capjack
22
,
Reference Pesme, Rozmus, Tikhonchuk, Maximov, Ourdev and Still
23
], laser-driven particle acceleration and radiation[
Reference Hu and Yi
24
–
Reference Li, Liu, Chen, Wu, Wang, Lu, Li, Ge, Yuan, Yan, Chen, Sheng and Zhang
30
], and the generation of intense magnetic fields[
Reference Shi, Arefiev, Hao and Zheng
31
,
Reference Ping, Zhong, Wang, Han, Sun, Zhang, Yuan, Xing, Wang, Liu, Zhang, Qiao, Zhang, Li, Zhu, Zhao and Zhang
32
].
$\%$
higher. The amplification effect of the seed laser intensity is remarkable, and the mergence length is tunable in a wide laser–plasma parameter range. This might provide a feasible routine to manipulate the propagation of multiple relativistic laser pulses for applications such as plasma optics[
Reference Myatt, Pesme, Hüller, Maximov, Rozmus and Capjack
22
,
Reference Pesme, Rozmus, Tikhonchuk, Maximov, Ourdev and Still
23
], laser-driven particle acceleration and radiation[
Reference Hu and Yi
24
–
Reference Li, Liu, Chen, Wu, Wang, Lu, Li, Ge, Yuan, Yan, Chen, Sheng and Zhang
30
], and the generation of intense magnetic fields[
Reference Shi, Arefiev, Hao and Zheng
31
,
Reference Ping, Zhong, Wang, Han, Sun, Zhang, Yuan, Xing, Wang, Liu, Zhang, Qiao, Zhang, Li, Zhu, Zhao and Zhang
32
].
In Section 2, we firstly review the propagation properties of two laser beams in plasma by the nonlinear Schrödinger equations (NSEs). Then we investigate the beam propagation dynamics by two-dimensional (2D) particle-in-cell (PIC) simulations, and reveal the reasons for attraction, repulsion and energy transfer between the two laser beams at different phase differences. In Section 3, two methods are proposed to manipulate the energy mergence process of fs seed lasers by using obliquely incident guiding lasers with different phase differences. Section 4 shows the influence of the laser–plasma parameters on the peak intensity of the merged light and the experimental consideration. Finally, a summary is given in Section 5.
2 Propagation of two parallel femtosecond laser beams in underdense plasmas
When a relativistically intense linearly polarized (LP) or circularly polarized (CP) laser pulse travels through underdense plasma along the
![]() $x$
direction, assuming that the ions are immobile, its envelope evolution can be described by the NSEs[
Reference Ren, Hemker, Fonseca, Duda and Mori
11
–
Reference Dong, Sheng and Zhang
16
,
Reference Huang, Zhou, Robinson, Qiao, Zhang, Wu, Zhuo, Norreys and He
33
,
Reference Bai, Zhou, Huang, Ju, Wu, Zhang, Yu, Qiao, Ruan and He
34
]:
$x$
direction, assuming that the ions are immobile, its envelope evolution can be described by the NSEs[
Reference Ren, Hemker, Fonseca, Duda and Mori
11
–
Reference Dong, Sheng and Zhang
16
,
Reference Huang, Zhou, Robinson, Qiao, Zhang, Wu, Zhuo, Norreys and He
33
,
Reference Bai, Zhou, Huang, Ju, Wu, Zhang, Yu, Qiao, Ruan and He
34
]:
 $$\begin{align}2{ik}_0\frac{\partial }{\partial x}a+{\nabla}_{\perp}^2a+{k}_{\mathrm{p}}^2\left(1-\frac{n}{\gamma}\right)a=0,\end{align}$$
$$\begin{align}2{ik}_0\frac{\partial }{\partial x}a+{\nabla}_{\perp}^2a+{k}_{\mathrm{p}}^2\left(1-\frac{n}{\gamma}\right)a=0,\end{align}$$
where
![]() $a= eE/{m}_{\mathrm{e}}{\omega}_0c$
is the normalized laser amplitude,
$a= eE/{m}_{\mathrm{e}}{\omega}_0c$
is the normalized laser amplitude,
![]() $-e$
,
$-e$
,
![]() ${m}_{\mathrm{e}}$
and
${m}_{\mathrm{e}}$
and
![]() $c$
are the charge, rest mass and light speed in vacuum, respectively,
$c$
are the charge, rest mass and light speed in vacuum, respectively,
![]() $E$
,
$E$
,
![]() ${\omega}_0$
and
${\omega}_0$
and
![]() ${k}_0={\omega}_0/c$
are the electric field, frequency and wave vector of the incident laser, respectively,
${k}_0={\omega}_0/c$
are the electric field, frequency and wave vector of the incident laser, respectively,
![]() $\gamma$
is the relativistic factor of the electron, which is
$\gamma$
is the relativistic factor of the electron, which is
![]() $\sqrt{1+{a}^2}$
and
$\sqrt{1+{a}^2}$
and
![]() $\sqrt{1+{a}^2/2}$
for the CP and LP lasers, respectively,
$\sqrt{1+{a}^2/2}$
for the CP and LP lasers, respectively,
![]() ${k}_{\mathrm{p}}={\omega}_{\mathrm{p}}/c$
and
${k}_{\mathrm{p}}={\omega}_{\mathrm{p}}/c$
and
![]() ${\omega}_{\mathrm{p}}=\sqrt{n_{\mathrm{e}}{e}^2/{\varepsilon}_0{m}_{\mathrm{e}}}$
are the plasma wave vector and frequency, respectively,
${\omega}_{\mathrm{p}}=\sqrt{n_{\mathrm{e}}{e}^2/{\varepsilon}_0{m}_{\mathrm{e}}}$
are the plasma wave vector and frequency, respectively,
![]() ${\varepsilon}_0$
is the vacuum permittivity and
${\varepsilon}_0$
is the vacuum permittivity and
![]() $n$
is the plasma electron density normalized by the initial electron density
$n$
is the plasma electron density normalized by the initial electron density
![]() ${n}_0$
. For two parallel incident Gaussian lasers with the same amplitude
${n}_0$
. For two parallel incident Gaussian lasers with the same amplitude
![]() ${a}_0$
,
${a}_0$
,
![]() $a={a}_1+{a}_2$
, where
$a={a}_1+{a}_2$
, where
![]() ${a}_1={a}_0\exp \left\{-\left[{z}^2+{\left(y-d/2\right)}^2/{r}_0^2\right]\right\}$
and
${a}_1={a}_0\exp \left\{-\left[{z}^2+{\left(y-d/2\right)}^2/{r}_0^2\right]\right\}$
and
![]() ${a}_2={a}_0\exp \left\{-\left[{z}^2+{\left(y+d/2\right)}^2/{r}_0^2\right]+i\Delta \phi \right\}$
, where
${a}_2={a}_0\exp \left\{-\left[{z}^2+{\left(y+d/2\right)}^2/{r}_0^2\right]+i\Delta \phi \right\}$
, where
![]() $\Delta \phi$
,
$\Delta \phi$
,
![]() ${r}_0$
and
${r}_0$
and
![]() $d$
are the initial phase difference, focal spot radius and spatial distance, respectively, of the two laser beams. Assuming that the amplitude envelope changes slowly and the energy transfer rate is constant, the NSEs can be approximated to the following[
Reference Sun, Edward, Lee and Parvez
13
,
Reference Bai, Zhou, Huang, Ju, Wu, Zhang, Yu, Qiao, Ruan and He
34
]:
$d$
are the initial phase difference, focal spot radius and spatial distance, respectively, of the two laser beams. Assuming that the amplitude envelope changes slowly and the energy transfer rate is constant, the NSEs can be approximated to the following[
Reference Sun, Edward, Lee and Parvez
13
,
Reference Bai, Zhou, Huang, Ju, Wu, Zhang, Yu, Qiao, Ruan and He
34
]:
 $$\begin{align}\frac{\partial }{\partial x}\left|{a}^2\right|=\frac{1}{\kappa}\sqrt{\frac{1}{2\pi }}{a}_0^2\exp \left(-\frac{d^2}{2{r}_0^2}\right)\left(\sin \Delta \phi \right)\frac{d}{k_0{r}_0^3},\end{align}$$
$$\begin{align}\frac{\partial }{\partial x}\left|{a}^2\right|=\frac{1}{\kappa}\sqrt{\frac{1}{2\pi }}{a}_0^2\exp \left(-\frac{d^2}{2{r}_0^2}\right)\left(\sin \Delta \phi \right)\frac{d}{k_0{r}_0^3},\end{align}$$
when the density modulation and relativistic electron mass correction are neglected, where
![]() $\kappa$
is 0.5 and 1 for the LP and CP laser pulses, respectively. Although Equation (2) ignores the laser–plasma interaction process, it could predict the possible propagation behavior of two laser beams with different phase difference in the plasma, and could provide reference for the parametric setting of the following PIC simulations. From Equation (2), we see that the energy transfer
$\kappa$
is 0.5 and 1 for the LP and CP laser pulses, respectively. Although Equation (2) ignores the laser–plasma interaction process, it could predict the possible propagation behavior of two laser beams with different phase difference in the plasma, and could provide reference for the parametric setting of the following PIC simulations. From Equation (2), we see that the energy transfer
![]() $\partial {\left|a\right|}^2/\partial x$
between the two lasers is a sinusoidal function of
$\partial {\left|a\right|}^2/\partial x$
between the two lasers is a sinusoidal function of
![]() $\Delta \phi$
, and reaches its maximum value at
$\Delta \phi$
, and reaches its maximum value at
![]() $\Delta \phi =\pi /2$
. When
$\Delta \phi =\pi /2$
. When
![]() $\Delta \phi =0$
and
$\Delta \phi =0$
and
![]() $\Delta \phi =\pi$
, there is no energy transfer. Whether they attract or repel each other can be shown by PIC simulations. In fact, the actual phase difference depends not only on
$\Delta \phi =\pi$
, there is no energy transfer. Whether they attract or repel each other can be shown by PIC simulations. In fact, the actual phase difference depends not only on
![]() $\Delta \phi$
, but also on the energy transfer situation. The laser phase velocity in plasma can be written by
$\Delta \phi$
, but also on the energy transfer situation. The laser phase velocity in plasma can be written by
![]() ${v}_{\mathrm{p}}=c/\sqrt{1-n/\gamma {n}_{\mathrm{c}}}$
, where
${v}_{\mathrm{p}}=c/\sqrt{1-n/\gamma {n}_{\mathrm{c}}}$
, where
![]() ${n}_{\mathrm{c}}$
is the critical density of plasmas. When the energy transfer occurs between beams, the phase velocity of the laser that obtains energy decreases since
${n}_{\mathrm{c}}$
is the critical density of plasmas. When the energy transfer occurs between beams, the phase velocity of the laser that obtains energy decreases since
![]() $\gamma$
actually becomes larger. In contrast,
$\gamma$
actually becomes larger. In contrast,
![]() ${v}_{\mathrm{p}}$
of the other beam is reduced, resulting in a change in the phase difference. In turn, the energy transfer will be affected. Note that the above equation can only give the steady-state solution, and is not suitable for characterizing the unsteady ultrafast process of short fs laser pulses propagating through underdense plasmas. In addition, it is also not valid for predicting accurately how much energy is transferred since the density modulation and relativistic electron mass correction become dominant in the relativistic regime.
${v}_{\mathrm{p}}$
of the other beam is reduced, resulting in a change in the phase difference. In turn, the energy transfer will be affected. Note that the above equation can only give the steady-state solution, and is not suitable for characterizing the unsteady ultrafast process of short fs laser pulses propagating through underdense plasmas. In addition, it is also not valid for predicting accurately how much energy is transferred since the density modulation and relativistic electron mass correction become dominant in the relativistic regime.
To illustrate the dynamics of two fs laser beams interacting with underdense plasmas, we perform 2D-PIC simulations by utilizing the code EPOCH[
Reference Arber, Bennett, Brady, Lawrence-Douglas, Ramsay, Sircombe, Gillies, Evans, Schmitz, Bell and Ridgers
35
]. The size of simulation box is
![]() $x\times y=80{\lambda}_0\times 70{\lambda}_0$
with 20 cells per wavelength, where
$x\times y=80{\lambda}_0\times 70{\lambda}_0$
with 20 cells per wavelength, where
![]() ${\lambda}_0=1\kern0.22em \mu \mathrm{m}$
is the laser wavelength. The fully ionized, uniform hydrogen plasma target is placed
${\lambda}_0=1\kern0.22em \mu \mathrm{m}$
is the laser wavelength. The fully ionized, uniform hydrogen plasma target is placed
![]() $x=\left[10,70\right]\kern0.22em \mu \mathrm{m}$
and
$x=\left[10,70\right]\kern0.22em \mu \mathrm{m}$
and
![]() $y=\left[-30,30\right]\kern0.22em \mu \mathrm{m}$
with the initial density of
$y=\left[-30,30\right]\kern0.22em \mu \mathrm{m}$
with the initial density of
![]() ${n}_{\mathrm{e}}={n}_{\mathrm{p}}=0.1{n}_{\mathrm{c}}$
. Each cell has 80 macroparticles, including 40 electrons and 40 protons. Two transverse Gaussian CP laser pulses of
${n}_{\mathrm{e}}={n}_{\mathrm{p}}=0.1{n}_{\mathrm{c}}$
. Each cell has 80 macroparticles, including 40 electrons and 40 protons. Two transverse Gaussian CP laser pulses of
![]() ${r}_0=2\kern0.22em \mu \mathrm{m}$
and
${r}_0=2\kern0.22em \mu \mathrm{m}$
and
![]() $d=4\kern0.22em \mu \mathrm{m}$
are normally incident from the left-hand boundary of the box and are focused on the front surface of the target. The initial phases of the upper and lower lasers are 0 and
$d=4\kern0.22em \mu \mathrm{m}$
are normally incident from the left-hand boundary of the box and are focused on the front surface of the target. The initial phases of the upper and lower lasers are 0 and
![]() $\Delta \phi$
, respectively. The laser has a temporal profile of
$\Delta \phi$
, respectively. The laser has a temporal profile of
![]() ${\sin}^2\left(\pi t/2{\tau}_0\right)$
, where
${\sin}^2\left(\pi t/2{\tau}_0\right)$
, where
![]() ${\tau}_0=15{T}_0$
and
${\tau}_0=15{T}_0$
and
![]() ${T}_0=3.3\kern0.22em \mathrm{fs}$
are the laser duration and period, respectively. Here,
${T}_0=3.3\kern0.22em \mathrm{fs}$
are the laser duration and period, respectively. Here,
![]() ${a}_0=1.9$
, corresponding to an intensity of
${a}_0=1.9$
, corresponding to an intensity of
![]() $I={a}_0^2\times {I}_0=9.89\times {10}^{18}\kern0.1em \mathrm{W}/{\mathrm{cm}}^2$
, where
$I={a}_0^2\times {I}_0=9.89\times {10}^{18}\kern0.1em \mathrm{W}/{\mathrm{cm}}^2$
, where
![]() ${I}_0=2.74\times {10}^{18}\kern0.1em \mathrm{W}/{\mathrm{cm}}^2$
. The open boundary conditions are used for fields and particles.
${I}_0=2.74\times {10}^{18}\kern0.1em \mathrm{W}/{\mathrm{cm}}^2$
. The open boundary conditions are used for fields and particles.
Figure 1 shows the distribution of the normalized light intensity
![]() $I/{I}_0$
for different initial
$I/{I}_0$
for different initial
![]() $\Delta \phi$
. We see that the two in-phase lasers of
$\Delta \phi$
. We see that the two in-phase lasers of
![]() $\Delta \phi =0$
(case 1) attracted each other, and merged into a single one with the peak intensity amplified by a factor of about 2.7 compared to the incident laser, while they will repel each other and gradually dissipate their energy during the propagation when
$\Delta \phi =0$
(case 1) attracted each other, and merged into a single one with the peak intensity amplified by a factor of about 2.7 compared to the incident laser, while they will repel each other and gradually dissipate their energy during the propagation when
![]() $\Delta \phi =\pi$
. At
$\Delta \phi =\pi$
. At
![]() $\Delta \phi =\pi /2$
, we find that the energy is transferred from the phase-advancing laser (lower) to the phase-delayed (upper) laser, resulting in an asymmetric distribution of light intensity. In fact, when
$\Delta \phi =\pi /2$
, we find that the energy is transferred from the phase-advancing laser (lower) to the phase-delayed (upper) laser, resulting in an asymmetric distribution of light intensity. In fact, when
![]() $0<\Delta \phi< \pi /2$
, the two laser beams not only attract each other, but also transfer energy. When
$0<\Delta \phi< \pi /2$
, the two laser beams not only attract each other, but also transfer energy. When
![]() $\pi /2<\Delta \phi< \pi$
, the repulsion and energy transfer of the two beams also coexist. From Figures 1(d)–1(f), we note that a mutual repulsion also occurs after
$\pi /2<\Delta \phi< \pi$
, the repulsion and energy transfer of the two beams also coexist. From Figures 1(d)–1(f), we note that a mutual repulsion also occurs after
![]() $t=60{T}_0$
. This is attributed to the amplitude
$t=60{T}_0$
. This is attributed to the amplitude
![]() $a$
of the two laser beams no longer being the same due to the energy transfer, and the phase speed is thus different since
$a$
of the two laser beams no longer being the same due to the energy transfer, and the phase speed is thus different since
![]() ${v}_{\mathrm{p}}\approx c\left(1+{n}_{\mathrm{e}}/2{an}_{\mathrm{c}}\right)$
. The actual phase difference between two laser beams will range from
${v}_{\mathrm{p}}\approx c\left(1+{n}_{\mathrm{e}}/2{an}_{\mathrm{c}}\right)$
. The actual phase difference between two laser beams will range from
![]() $\pi /2$
to
$\pi /2$
to
![]() $\pi$
. As a result, early on, the two beams begin to repel each other, leading their transverse distance to grow larger. Then they travel separately until their energies are completely depleted.
$\pi$
. As a result, early on, the two beams begin to repel each other, leading their transverse distance to grow larger. Then they travel separately until their energies are completely depleted.

Figure 1 Snapshot of spatial distribution of the normalized light intensity
![]() $I/{I}_0$
of two parallel incident seed lasers with different initial phase difference of (a)–(c)
$I/{I}_0$
of two parallel incident seed lasers with different initial phase difference of (a)–(c)
![]() $\Delta \phi =0$
, (d)–(f)
$\Delta \phi =0$
, (d)–(f)
![]() $\Delta \phi =\pi /2$
and (g)–(i)
$\Delta \phi =\pi /2$
and (g)–(i)
![]() $\Delta \phi =\pi$
at different times. The arrows in the left-column panels represent the Poynting vector of the lasers.
$\Delta \phi =\pi$
at different times. The arrows in the left-column panels represent the Poynting vector of the lasers.
We can understand the interaction mechanism of two laser beams in underdense plasmas through the electron dynamics. The light propagation in a medium is closely related to its refractive index
![]() $N=\sqrt{1-{n}_{\mathrm{e}}/\gamma {n}_{\mathrm{c}}}$
. From Figures 2(a)–2(c), we can observe that the ponderomotive force of the laser
$N=\sqrt{1-{n}_{\mathrm{e}}/\gamma {n}_{\mathrm{c}}}$
. From Figures 2(a)–2(c), we can observe that the ponderomotive force of the laser
![]() ${f}_{\mathrm{p}}$
(
${f}_{\mathrm{p}}$
(
![]() ${f}_{\mathrm{p}}\propto \partial {a}^2/\partial r$
, where
${f}_{\mathrm{p}}\propto \partial {a}^2/\partial r$
, where
![]() $r=\sqrt{x^2+{y}^2}$
)[
Reference Bauer, Mulser and Steeb
36
] drives the electrons away from the central region, forming two hollow density channels. When
$r=\sqrt{x^2+{y}^2}$
)[
Reference Bauer, Mulser and Steeb
36
] drives the electrons away from the central region, forming two hollow density channels. When
![]() $\Delta \phi =0$
, the ponderomotive force pushes the electrons sideways toward the same directions. The current element direction at the same
$\Delta \phi =0$
, the ponderomotive force pushes the electrons sideways toward the same directions. The current element direction at the same
![]() $x$
position driven by two seed lasers is therefore identical, as shown in Figure 2(d), and thus they appear to attract each other according to Ampere’s law. Under the synergistic expulsion of the two beams, a small density cavity is formed (see the white dotted box), which acts as an energy storage container and in turn promotes the mergence of two laser beams since
$x$
position driven by two seed lasers is therefore identical, as shown in Figure 2(d), and thus they appear to attract each other according to Ampere’s law. Under the synergistic expulsion of the two beams, a small density cavity is formed (see the white dotted box), which acts as an energy storage container and in turn promotes the mergence of two laser beams since
![]() $N$
becomes smaller inside the cavity. At
$N$
becomes smaller inside the cavity. At
![]() $\Delta \phi =\pi$
, the current element direction at the same
$\Delta \phi =\pi$
, the current element direction at the same
![]() $x$
position is opposite, as seen in Figure 2(f), and they behave as mutually repellent. Note that a portion of the electrons are piled up in the region of
$x$
position is opposite, as seen in Figure 2(f), and they behave as mutually repellent. Note that a portion of the electrons are piled up in the region of
![]() $-3{\lambda}_0<y<3{\lambda}_0$
due to the inward squeeze of the ponderomotive force of two seed lasers. The electron density in the middle is thus greater than that on both sides and the two lasers begin to deflect outward due to the difference in refractive index. The repulsive effect is further enhanced and the actual gap between the two channels becomes larger as they propagate separately in their own half space. Here,
$-3{\lambda}_0<y<3{\lambda}_0$
due to the inward squeeze of the ponderomotive force of two seed lasers. The electron density in the middle is thus greater than that on both sides and the two lasers begin to deflect outward due to the difference in refractive index. The repulsive effect is further enhanced and the actual gap between the two channels becomes larger as they propagate separately in their own half space. Here,
![]() $\Delta \phi =\pi /2$
could be regarded as a dividing point at which the beam attracts and repels. When
$\Delta \phi =\pi /2$
could be regarded as a dividing point at which the beam attracts and repels. When
![]() $\Delta \phi$
is farther away from
$\Delta \phi$
is farther away from
![]() $\pi /2$
and toward 0 or
$\pi /2$
and toward 0 or
![]() $\pi$
, the attraction or repulsion effect is more significant, and the energy transfer becomes weaker. At
$\pi$
, the attraction or repulsion effect is more significant, and the energy transfer becomes weaker. At
![]() $\Delta \phi =\pi /2$
, a lot of transverse sloping upward gaps (represented by the white arrows) are induced, as shown in Figures 2(b) and 2(e). A portion of the phase-advancing laser energy reflected by the dense boundaries at the bottom flows into the phase-delayed laser-induced channel by these gaps, which is the direct reason for the energy transfer. It should be mentioned that the accumulation of electrons does not occur only in 2D geometry. We performed three-dimensional (3D)-PIC simulation and found similar features. The slight difference is that the filamentous structure of electron density (seen in Figures 2(a)–2(c)) resulting from the electrons oscillating in the laser electric field is no longer significant.
$\Delta \phi =\pi /2$
, a lot of transverse sloping upward gaps (represented by the white arrows) are induced, as shown in Figures 2(b) and 2(e). A portion of the phase-advancing laser energy reflected by the dense boundaries at the bottom flows into the phase-delayed laser-induced channel by these gaps, which is the direct reason for the energy transfer. It should be mentioned that the accumulation of electrons does not occur only in 2D geometry. We performed three-dimensional (3D)-PIC simulation and found similar features. The slight difference is that the filamentous structure of electron density (seen in Figures 2(a)–2(c)) resulting from the electrons oscillating in the laser electric field is no longer significant.

Figure 2 Snapshots of spatial distribution of the electron density
![]() ${n}_{\mathrm{e}}/{n}_{\mathrm{c}}$
(a)–(c) and the current density
${n}_{\mathrm{e}}/{n}_{\mathrm{c}}$
(a)–(c) and the current density
![]() $j/{j}_0$
(d)–(f) at different times for two parallel incident seed lasers of (a), (d)
$j/{j}_0$
(d)–(f) at different times for two parallel incident seed lasers of (a), (d)
![]() $\Delta \phi =0$
, (b), (e)
$\Delta \phi =0$
, (b), (e)
![]() $\pi /2$
and (c), (f)
$\pi /2$
and (c), (f)
![]() $\pi$
, respectively. Here, the current density is normalized by
$\pi$
, respectively. Here, the current density is normalized by
![]() ${j}_0=1\times {10}^{16}\ \mathrm{A}/{\mathrm{cm}}^2$
and
${j}_0=1\times {10}^{16}\ \mathrm{A}/{\mathrm{cm}}^2$
and
![]() ${I}_0=2.74\times {10}^{18}\kern0.1em \mathrm{W}/{\mathrm{cm}}^2$
.
${I}_0=2.74\times {10}^{18}\kern0.1em \mathrm{W}/{\mathrm{cm}}^2$
.
3 Manipulation energy mergence by obliquely incident external guiding lasers
As discussed above, the actual phase difference between two lasers determines their propagation properties in underdense plasma. In fact, in addition to changing
![]() $\Delta \phi$
and
$\Delta \phi$
and
![]() $N$
, the real phase difference can also be modulated with an obliquely incident laser. For one of the two beams obliquely incident at an incident angle
$N$
, the real phase difference can also be modulated with an obliquely incident laser. For one of the two beams obliquely incident at an incident angle
![]() $\theta$
, as the parallel beam travels
$\theta$
, as the parallel beam travels
![]() $L$
distance, the resulting phase difference
$L$
distance, the resulting phase difference
![]() $\Delta \psi$
can be expressed as follows:
$\Delta \psi$
can be expressed as follows:
 $$\begin{align}\Delta \psi =2\pi N\left[L\left(\frac{1}{\cos \theta }-1\right)\right]/{\lambda}_0.\end{align}$$
$$\begin{align}\Delta \psi =2\pi N\left[L\left(\frac{1}{\cos \theta }-1\right)\right]/{\lambda}_0.\end{align}$$
Here, we propose two possible methods to manipulate the energy mergence between two parallel fs seed lasers of
![]() ${\Delta \phi =0}$
by obliquely incident external guiding beamlets. The first method is to use two guiding lasers of
${\Delta \phi =0}$
by obliquely incident external guiding beamlets. The first method is to use two guiding lasers of
![]() $\Delta \varphi =\pi$
with an incident angle
$\Delta \varphi =\pi$
with an incident angle
![]() $\theta =6{}^{\circ}$
(the optimal angle for obtaining the highest intensity of the merged laser) relative to the seed lasers (case 3), where
$\theta =6{}^{\circ}$
(the optimal angle for obtaining the highest intensity of the merged laser) relative to the seed lasers (case 3), where
![]() $\Delta \varphi$
is the initial phase difference between the guiding and seed lasers. For comparison, we also perform the case of the parallel guiding lasers (
$\Delta \varphi$
is the initial phase difference between the guiding and seed lasers. For comparison, we also perform the case of the parallel guiding lasers (
![]() $\theta =0{}^{\circ}$
, case 2). Figure 3 shows the distribution of the normalized laser intensity
$\theta =0{}^{\circ}$
, case 2). Figure 3 shows the distribution of the normalized laser intensity
![]() $I/{I}_0$
in cases 2 and 3. With respect to Figure 1(b), we can see that the merging process of the seed lasers becomes earlier due to the repulsion effect of two external guiding lasers in both cases. In case 2, since the guiding laser energy is eventually consumed, their energy does not participate in the coupling of the seed laser, resulting in the intensity of the merged laser being comparable to that in case 1. However, for case 3, we find that the mergence time and distance of the seed lasers are slightly shortened, and the merging effect is significantly strengthened. This is because the repulsion and energy transfer from the seed lasers occur simultaneously since the actual phase difference between the guiding and seed lasers is slightly less than
$I/{I}_0$
in cases 2 and 3. With respect to Figure 1(b), we can see that the merging process of the seed lasers becomes earlier due to the repulsion effect of two external guiding lasers in both cases. In case 2, since the guiding laser energy is eventually consumed, their energy does not participate in the coupling of the seed laser, resulting in the intensity of the merged laser being comparable to that in case 1. However, for case 3, we find that the mergence time and distance of the seed lasers are slightly shortened, and the merging effect is significantly strengthened. This is because the repulsion and energy transfer from the seed lasers occur simultaneously since the actual phase difference between the guiding and seed lasers is slightly less than
![]() $\pi$
in the initial stage. It should be noted that the energy obtained from the guiding lasers is transmitting off-axis, so that the merged light disperses around at a later time.
$\pi$
in the initial stage. It should be noted that the energy obtained from the guiding lasers is transmitting off-axis, so that the merged light disperses around at a later time.

Figure 3 Snapshot of spatial distribution of the normalized light intensity
![]() $I/{I}_0$
at different times using two external guiding lasers of initial phases advancing
$I/{I}_0$
at different times using two external guiding lasers of initial phases advancing
![]() $\pi$
compared to seed lasers (i.e.,
$\pi$
compared to seed lasers (i.e.,
![]() $\Delta \varphi =\pi$
) with the incidence angle of
$\Delta \varphi =\pi$
) with the incidence angle of
![]() $\theta =0{}^{\circ}$
((a)–(c), case 2) and
$\theta =0{}^{\circ}$
((a)–(c), case 2) and
![]() $\theta =6{}^{\circ}$
((d)–(f), case 3), respectively. The initial phase difference of the seed lasers is
$\theta =6{}^{\circ}$
((d)–(f), case 3), respectively. The initial phase difference of the seed lasers is
![]() $\Delta \phi =0$
.
$\Delta \phi =0$
.
Another method is to employ two guiding lasers of
![]() ${\Delta \varphi =\pi /2}$
. We still consider parallel incidence (
${\Delta \varphi =\pi /2}$
. We still consider parallel incidence (
![]() $\theta =0{}^{\circ}$
, case 4) and oblique incidence at a small angle of
$\theta =0{}^{\circ}$
, case 4) and oblique incidence at a small angle of
![]() $\theta =5{}^{\circ}$
(case 5), which corresponds to the optimal angle for obtaining the highest intensity of the merged light. Compared with case 1, it is found that the intensity of the merged light is stronger in case 4 because of the energy transfer from the guiding laser to the neighboring seed laser, as presented in Figure 4(a). Accompanied by the laser propagation, the actual phase difference between the guiding laser and seed laser gradually exceeds
$\theta =5{}^{\circ}$
(case 5), which corresponds to the optimal angle for obtaining the highest intensity of the merged light. Compared with case 1, it is found that the intensity of the merged light is stronger in case 4 because of the energy transfer from the guiding laser to the neighboring seed laser, as presented in Figure 4(a). Accompanied by the laser propagation, the actual phase difference between the guiding laser and seed laser gradually exceeds
![]() $\pi /2$
, and the inner in-phase seed lasers begin to merge aided by the repulsion of the guiding lasers in Figures 4(b) and 4(c). The peak intensity of the merged light is thus obviously higher than that in cases 1 and 2. Figures 4(d)–4(f) show that the energy merging of seed lights is more effective as the guiding lasers are obliquely incident. The guiding laser and its adjacent seed laser begin to merge earlier, avoiding more energy loss during the propagation process, as seen in Figure 4(d). Subsequently, they undergo a secondary mergence into a single beam of light and the overall mergence time and distance are obviously extended, as shown in Figure 4(f).
$\pi /2$
, and the inner in-phase seed lasers begin to merge aided by the repulsion of the guiding lasers in Figures 4(b) and 4(c). The peak intensity of the merged light is thus obviously higher than that in cases 1 and 2. Figures 4(d)–4(f) show that the energy merging of seed lights is more effective as the guiding lasers are obliquely incident. The guiding laser and its adjacent seed laser begin to merge earlier, avoiding more energy loss during the propagation process, as seen in Figure 4(d). Subsequently, they undergo a secondary mergence into a single beam of light and the overall mergence time and distance are obviously extended, as shown in Figure 4(f).

Figure 4 Snapshot of spatial distribution of the normalized light intensity
![]() $I/{I}_0$
at different times using two external guiding lasers of initial phases advancing
$I/{I}_0$
at different times using two external guiding lasers of initial phases advancing
![]() $\pi /2$
compared to seed lasers (i.e.,
$\pi /2$
compared to seed lasers (i.e.,
![]() $\Delta \varphi =\pi /2$
) with the incidence angle of
$\Delta \varphi =\pi /2$
) with the incidence angle of
![]() $\theta =0{}^{\circ}$
((a)–(c), case 4) and
$\theta =0{}^{\circ}$
((a)–(c), case 4) and
![]() $\theta =5{}^{\circ}$
((d)–(f), case 5), respectively. The initial phase difference of the seed lasers is
$\theta =5{}^{\circ}$
((d)–(f), case 5), respectively. The initial phase difference of the seed lasers is
![]() $\Delta \phi =0$
.
$\Delta \phi =0$
.
When a relativistic fs laser pulse propagates through underdense plasma, the electron density will be significantly modulated, and nonlinear structures such as the electron cavity and channel may appear, which in turn will affect the subsequent propagation behavior of the laser. Figure 5 shows the electron density distribution at different times in the five cases. We see that a multi-cavity structure is induced in cases 1, 2 and 4, but without a large number of electrons injected into the tail of the cavities, which is different from the bubbles in the highly nonlinear broken-wave regime[
Reference Pukhov and Meyer-Ter-Vehn
37
]. In case 3, with the use of two obliquely incident guiding lasers of
![]() $\Delta \varphi =\pi$
, the merged light will break through the tail of the cavities to form a long plasma channel that can hold a large amount of laser energy. When
$\Delta \varphi =\pi$
, the merged light will break through the tail of the cavities to form a long plasma channel that can hold a large amount of laser energy. When
![]() $\Delta \varphi$
is reduced to
$\Delta \varphi$
is reduced to
![]() $\pi /2$
for case 5, two plasma channels are firstly formed at
$\pi /2$
for case 5, two plasma channels are firstly formed at
![]() $t=44{T}_0$
and then gradually evolve into two front and rear large size cavities at
$t=44{T}_0$
and then gradually evolve into two front and rear large size cavities at
![]() $t=76{T}_0$
, which is more beneficial for storing the light field energies.
$t=76{T}_0$
, which is more beneficial for storing the light field energies.

Figure 5 Snapshot of the normalized electron density
![]() ${n}_{\mathrm{e}}/{n}_{\mathrm{c}}$
for
${n}_{\mathrm{e}}/{n}_{\mathrm{c}}$
for
![]() $t=60{T}_0$
from case 1 to case 4, and for
$t=60{T}_0$
from case 1 to case 4, and for
![]() $t=44{T}_0$
and
$t=44{T}_0$
and
![]() $t=76{T}_0$
in case 5.
$t=76{T}_0$
in case 5.
Figures 6(a) and 6(b) show the axial profile of the merged light intensity along the
![]() $y=0$
direction and the transverse profile in the
$y=0$
direction and the transverse profile in the
![]() $x$
position, which corresponds to the peak intensity when the merged laser is strongest in the above five cases. For reference, the distribution of the seed lasers in the propagation axis and the transverse distribution at the peak intensity are also given. One can see that in cases 3 and 5, the peak intensity of the merged light
$x$
position, which corresponds to the peak intensity when the merged laser is strongest in the above five cases. For reference, the distribution of the seed lasers in the propagation axis and the transverse distribution at the peak intensity are also given. One can see that in cases 3 and 5, the peak intensity of the merged light
![]() ${I}_{\mathrm{m}}$
reaches
${I}_{\mathrm{m}}$
reaches
![]() $5.84\times {10}^{19}\kern0.1em$
and
$5.84\times {10}^{19}\kern0.1em$
and
![]() $5.12\times {10}^{19}\kern0.1em \mathrm{W}/{\mathrm{cm}}^2$
, respectively, which are the highest in all five cases. Compared to that of the seed laser, the light intensity can be amplified by more than five times, and the focused spot size is significantly reduced in both cases. The highest energy conversion efficiency
$5.12\times {10}^{19}\kern0.1em \mathrm{W}/{\mathrm{cm}}^2$
, respectively, which are the highest in all five cases. Compared to that of the seed laser, the light intensity can be amplified by more than five times, and the focused spot size is significantly reduced in both cases. The highest energy conversion efficiency
![]() $\eta$
from all incident lasers to the merged light in the five cases is displayed in Figure 6(c). We see that although the use of the guiding lasers brings more energy loss during the propagation,
$\eta$
from all incident lasers to the merged light in the five cases is displayed in Figure 6(c). We see that although the use of the guiding lasers brings more energy loss during the propagation,
![]() $\eta$
in cases 3 and 5 is still approximately 60
$\eta$
in cases 3 and 5 is still approximately 60
![]() $\%$
higher, which is comparable to case 1 of only two seed lasers. The energy conversion efficiency
$\%$
higher, which is comparable to case 1 of only two seed lasers. The energy conversion efficiency
![]() ${\eta}_{\mathrm{e}}$
from all incident lasers to the electrons in the five cases is given in Figure 6(d). Combining Figure 6(a), it is found that, except for case 2,
${\eta}_{\mathrm{e}}$
from all incident lasers to the electrons in the five cases is given in Figure 6(d). Combining Figure 6(a), it is found that, except for case 2,
![]() ${\eta}_{\mathrm{e}}$
is lower when
${\eta}_{\mathrm{e}}$
is lower when
![]() ${I}_{\mathrm{m}}$
is higher owing to the energy conservation. In case 2, the guiding lasers do not participate in the interaction between seed lasers, but rather lack the compressing or even breaking processes of the dense electron walls. They propagate almost independently on both sides, resulting in a lower proportion of energy transferred to the electrons. It should be mentioned that the sum of
${I}_{\mathrm{m}}$
is higher owing to the energy conservation. In case 2, the guiding lasers do not participate in the interaction between seed lasers, but rather lack the compressing or even breaking processes of the dense electron walls. They propagate almost independently on both sides, resulting in a lower proportion of energy transferred to the electrons. It should be mentioned that the sum of
![]() $\eta$
and the highest
$\eta$
and the highest
![]() ${\eta}_{\mathrm{e}}$
in Figures 6(c) and 6(d) is smaller than approximately 100
${\eta}_{\mathrm{e}}$
in Figures 6(c) and 6(d) is smaller than approximately 100
![]() $\%$
because the energy of the scattered light is not counted for
$\%$
because the energy of the scattered light is not counted for
![]() $\eta$
in Figure 6(c).
$\eta$
in Figure 6(c).

Figure 6 (a) The axial profile of laser intensity along the
![]() $y=0$
direction and (b) the transverse profile at the
$y=0$
direction and (b) the transverse profile at the
![]() $x$
position corresponding to the peak intensity when the merged light is strongest in the five cases. For comparison, the black lines in (a) and (b) give the axial and transverse profiles of the seed laser. (c) The highest energy conversion efficiency from all incident lasers to the merged light, and (d) the temporal evolution of the energy conversion efficiency from all incident lasers to the electrons in the five cases.
$x$
position corresponding to the peak intensity when the merged light is strongest in the five cases. For comparison, the black lines in (a) and (b) give the axial and transverse profiles of the seed laser. (c) The highest energy conversion efficiency from all incident lasers to the merged light, and (d) the temporal evolution of the energy conversion efficiency from all incident lasers to the electrons in the five cases.
Note that the mergence process above is investigated at the same intensity, so that the total laser energy used in cases 3 and 5 is twice that in case 1. In principle, a comparison at the same total laser energy is more instructive, but a comparison at the same intensity is also meaningful for manipulating relativistic fs lasers to achieve higher light intensities. In fact, a similar scenario occurs in direct-driven inertial confinement fusion, where multiple picosecond laser beams of the same intensity are incident to the center of a deuterium tritium pellet, and cross-beam energy transfer may occur in the laser–plasma interaction[
Reference Kirkwood, Afeyan, Kruer, MacGowan, Moody, Montgomery, Pennington, Weiland and Wilks
38
,
Reference Moody, Michel, Divol, Berger, Bond, Bradley, Callahan, Dewald, Dixit, Edwards, Glenn, Hamza, Haynam, Hinkel, Izumi, Jones, Kilkenny, Kirkwood, Kline, Kruer, Kyrala, Landen, LePape, Lindl, MacGowan, Meezan, Nikroo, Rosen, Schneider, Strozzi, Suter, Thomas, Town, Widmann, Williams, Atherton, Glenzer and Moses
39
]. Our paper focuses more on the situation of multiple fs lasers propagating in plasma. For cases 3 and 5, we also simulated the same laser energy as case 1, where the intensity of the seed and guiding lasers is reduced to half (i.e.,
![]() $I=4.945\times {10}^{18}\kern0.1em \mathrm{W}/{\mathrm{cm}}^2$
). It is found that both
$I=4.945\times {10}^{18}\kern0.1em \mathrm{W}/{\mathrm{cm}}^2$
). It is found that both
![]() ${I}_{\mathrm{m}}$
and
${I}_{\mathrm{m}}$
and
![]() $\eta$
are comparable for the three cases.
$\eta$
are comparable for the three cases.
4 Influence of the laser–plasma parameters on the intensity of the merged light
We next consider the influence of the amplification effect of laser intensity on the laser–plasma parameters. Since cases 3 and 5 are more advantageous in terms of energy mergence, we only show the simulation results of different parameters in these two cases. Figure 7 shows the dependence of the peak intensity of the merged laser
![]() ${I}_{\mathrm{m}}$
on
${I}_{\mathrm{m}}$
on
![]() ${I}_0$
,
${I}_0$
,
![]() $d$
,
$d$
,
![]() $\theta$
and
$\theta$
and
![]() ${n}_{\mathrm{e}}$
in cases 3 and 5. Other parameters are the same as the above as only one of the parameters varies. From Figure 7(a), we see that
${n}_{\mathrm{e}}$
in cases 3 and 5. Other parameters are the same as the above as only one of the parameters varies. From Figure 7(a), we see that
![]() ${I}_{\mathrm{m}}$
grows linearly with
${I}_{\mathrm{m}}$
grows linearly with
![]() ${I}_0$
in a wide intensity region, indicating that the amplification effect of our proposed methods is very robust. Here,
${I}_0$
in a wide intensity region, indicating that the amplification effect of our proposed methods is very robust. Here,
![]() $d$
plays a crucial role in the energy mergence of seed lasers. According to Equation (2), the energy transfer
$d$
plays a crucial role in the energy mergence of seed lasers. According to Equation (2), the energy transfer
![]() $\partial {\left|a\right|}^2/\partial x$
decreases exponentially with increasing
$\partial {\left|a\right|}^2/\partial x$
decreases exponentially with increasing
![]() $d$
, resulting in the reduction of
$d$
, resulting in the reduction of
![]() ${I}_{\mathrm{m}}$
. In Figure 7(b), it is found that the amplification effect indeed decreases significantly as
${I}_{\mathrm{m}}$
. In Figure 7(b), it is found that the amplification effect indeed decreases significantly as
![]() $d$
rises. When
$d$
rises. When
![]() $d\ge 6{\lambda}_0$
, the seed lasers hardly interact in the plasma, but rather propagate independently, so they cannot collapse into a beam of light. Here, we only simulate the case of
$d\ge 6{\lambda}_0$
, the seed lasers hardly interact in the plasma, but rather propagate independently, so they cannot collapse into a beam of light. Here, we only simulate the case of
![]() $d\ge 2{\lambda}_0$
since the interference effect of two laser beams will become dominant. The oblique incidence of the guide lasers is conducive to the energy mergence of the seed lasers, but to avoid their interaction time being too short, it is still limited to a small angle. Figure 7(c) indicates that the amplification effect is strengthened and the mergence time is earlier due to the repulsion of the guiding lasers as
$d\ge 2{\lambda}_0$
since the interference effect of two laser beams will become dominant. The oblique incidence of the guide lasers is conducive to the energy mergence of the seed lasers, but to avoid their interaction time being too short, it is still limited to a small angle. Figure 7(c) indicates that the amplification effect is strengthened and the mergence time is earlier due to the repulsion of the guiding lasers as
![]() $\theta$
increases in case 3. However, for case 5, the intensity of the merged light reduces as
$\theta$
increases in case 3. However, for case 5, the intensity of the merged light reduces as
![]() $\theta$
is larger because the cross-time between the guiding and seed lasers is so early that the energy transfer is insufficient. Here,
$\theta$
is larger because the cross-time between the guiding and seed lasers is so early that the energy transfer is insufficient. Here,
![]() ${n}_{\mathrm{e}}$
mainly determines the energy loss of the lasers in the plasmas. Figure 7(d) shows that for case 3, it is equivalent to the laser propagation in vacuum while
${n}_{\mathrm{e}}$
mainly determines the energy loss of the lasers in the plasmas. Figure 7(d) shows that for case 3, it is equivalent to the laser propagation in vacuum while
![]() ${n}_{\mathrm{e}}$
is low. According to Maxwell’s equations, there is no repulsion between the guiding and seed lasers. Nevertheless, as
${n}_{\mathrm{e}}$
is low. According to Maxwell’s equations, there is no repulsion between the guiding and seed lasers. Nevertheless, as
![]() ${n}_{\mathrm{e}}$
increases, both the guiding and seed lasers would lose more energy, weakening the amplification effect. Therefore, there is an optimal plasma density for given laser parameters. Note that in case 5, although all lasers have energy loss, the two guiding lasers continue to transfer their energies to the seed lasers and the amplification effect of light intensity is still significant.
${n}_{\mathrm{e}}$
increases, both the guiding and seed lasers would lose more energy, weakening the amplification effect. Therefore, there is an optimal plasma density for given laser parameters. Note that in case 5, although all lasers have energy loss, the two guiding lasers continue to transfer their energies to the seed lasers and the amplification effect of light intensity is still significant.

Figure 7 Dependence of the peak intensity of the merged light
![]() ${I}_{\mathrm{m}}$
on (a) the intensity of the incident seed laser
${I}_{\mathrm{m}}$
on (a) the intensity of the incident seed laser
![]() ${I}_0$
, (b) the transverse separation distance
${I}_0$
, (b) the transverse separation distance
![]() $d$
of the two seed lasers, (c) the incidence angle of the guiding laser
$d$
of the two seed lasers, (c) the incidence angle of the guiding laser
![]() $\theta$
and (d) the normalized electron density of plasma
$\theta$
and (d) the normalized electron density of plasma
![]() ${n}_{\mathrm{e}}/{n}_{\mathrm{c}}$
.
${n}_{\mathrm{e}}/{n}_{\mathrm{c}}$
.
In experiments, the plasma density uniformity, initial phase difference of the lasers and their focal point positions are difficult to control accurately. Therefore, it is essential to discuss the influence of these factors on the mergence effect. We consider two different plasma density distributions: (1) a preplasma with a length of 5 μm and a density rising linearly from
![]() $0.01{n}_{\mathrm{c}}$
to
$0.01{n}_{\mathrm{c}}$
to
![]() $0.1{n}_{\mathrm{c}}$
in front of a uniform target with a density of
$0.1{n}_{\mathrm{c}}$
in front of a uniform target with a density of
![]() $0.1{n}_{\mathrm{c}}$
; (2) a plasma target with a density linear increase from
$0.1{n}_{\mathrm{c}}$
; (2) a plasma target with a density linear increase from
![]() $0.05{n}_{\mathrm{c}}$
to
$0.05{n}_{\mathrm{c}}$
to
![]() $0.1{n}_{\mathrm{c}}$
over a length of 60 μm. It is found that the intensity of the merged light remains at a similar level compared to the homogeneous plasma, indicating that the plasma density distribution has little effect on the light mergence. When the initial phase difference (in case 3,
$0.1{n}_{\mathrm{c}}$
over a length of 60 μm. It is found that the intensity of the merged light remains at a similar level compared to the homogeneous plasma, indicating that the plasma density distribution has little effect on the light mergence. When the initial phase difference (in case 3,
![]() $\Delta \varphi$
between the lower seed and guiding lasers is adjusted to
$\Delta \varphi$
between the lower seed and guiding lasers is adjusted to
![]() $5\pi /6$
or
$5\pi /6$
or
![]() $7\pi /6$
; in case 5,
$7\pi /6$
; in case 5,
![]() $\Delta \varphi$
between the lower seed and guiding lasers is adjusted to
$\Delta \varphi$
between the lower seed and guiding lasers is adjusted to
![]() $\pi /3$
or
$\pi /3$
or
![]() $2\pi /3$
) and the distance (in cases 3 and 5,
$2\pi /3$
) and the distance (in cases 3 and 5,
![]() $d$
between the upper seed and guiding lasers is adjusted to 5 μm) between the seed and guiding lasers is slightly different, the distribution of light intensity is no longer symmetrical and may deviate from the
$d$
between the upper seed and guiding lasers is adjusted to 5 μm) between the seed and guiding lasers is slightly different, the distribution of light intensity is no longer symmetrical and may deviate from the
![]() $x$
direction due to the different mergence speeds between the beams.
$x$
direction due to the different mergence speeds between the beams.
5 Conclusion
In conclusion, we investigate the dynamics of multiple relativistic fs lasers propagating through underdense plasmas. The 2D-PIC simulation results show that the two seed lasers with different initial phase differences exhibit different behaviors, such as attraction, repulsion and energy transfer. Based on this, two possible methods to manipulate the energy mergence of seed lasers are proposed to utilize two external obliquely incident guiding lasers with their initial phases advancing
![]() $\pi$
or
$\pi$
or
![]() $\pi /2$
compared to the seed lasers. Compared to the seed laser, more than five times light intensity amplification can be realized, and the energy conversion efficiency from all incident lasers to merged light is approximately 60
$\pi /2$
compared to the seed lasers. Compared to the seed laser, more than five times light intensity amplification can be realized, and the energy conversion efficiency from all incident lasers to merged light is approximately 60
![]() $\%$
higher. The results are helpful for understanding the propagation feature of multiple ultraintense ultrashort laser pulses in plasmas, and are potentially useful for related applications, for example, plasma-based nonlinear optics, generation of energetic particles and extremely intense electromagnetic fields.
$\%$
higher. The results are helpful for understanding the propagation feature of multiple ultraintense ultrashort laser pulses in plasmas, and are potentially useful for related applications, for example, plasma-based nonlinear optics, generation of energetic particles and extremely intense electromagnetic fields.
Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant Nos. 12175310, 12275356, 12135009 and 12075157) and the Natural Science Foundation of Hunan Province (Grant No. 2022JJ20042).