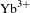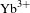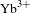Modeling of the 3D spatio-temporal thermal profile of joule-class $\text{Yb}^{3+}$-based laser amplifiers

Abstract

Thermal profile modification of an active material in a laser amplifier via optical pumping results in a change in the material’s refractive index, and causes thermal expansion and stress, eventually leading to spatial phase aberrations, or even permanent material damage. For this purpose, knowledge of the 3D spatio-temporal thermal profile, which can currently only be retrieved via numerical simulations, is critical for joule-class laser amplifiers to reveal potentially dangerous thermal features within the pumped active materials. In this investigation, a detailed, spatio-temporal numerical simulation was constructed and tested for accuracy against surface thermal measurements of various end-pumped $\text{Yb}^{3+}$-doped laser-active materials. The measurements and simulations show an excellent agreement and the model was successfully applied to a joule-class $\text{Yb}^{3+}$-based amplifier currently operating in the POLARIS laser system at the Friedrich-Schiller-University and Helmholtz-Institute Jena in Germany.

1 Introduction

Advances in relativistic laser plasma physics are reliant on the optimization of state-of-the-art laser systems toward higher peak and average powers. These laser pulses, when focused to intensities in excess of $10^{20}~\text{W}/\text{cm}^{2}$ , can accelerate electrons^[1] and ions^[2] to relativistic velocities, as well as generate X-rays^[3] and high harmonics^[4]. Attaining and increasing such laser intensities requires the proper design, characterization, and optimization of the final multi-pass amplifier stages to amplify the seed laser pulse well into the multi-joule regime while maintaining its spatial and temporal fidelity.

Within these final multi-pass amplifier setups, large beam diameters are necessary to reduce the fluence of the laser pulse below the laser-induced damage threshold (LIDT) of the active materials. Consequently, these large beam profiles are particularly susceptible to effects leading to wavefront aberrations, the ramifications of which are prominent due to the long propagation distances typically found in nonimaging joule-level multi-pass amplifiers. Such wavefront aberrations occur in part due to the quantum defect, in which a portion of the pump laser energy is transferred to the active material in the form of heat, resulting in a change in the temperature profile that forms within the timescale of the pump pulse. This pump-induced temperature change causes a modification of the refractive index^[5], leads to thermal expansion and stress, and alters the emission and absorption spectra^[6] of the laser material.

To mitigate the impact of these effects, narrowband diode-pumped $\text{Yb}^{3+}$ -doped active materials can be employed, which can provide a significantly lower quantum defect of 9%^[6] when compared to other dopants, such as $\text{Nd}^{3+}$ (24%^[7]) or $\text{Ti}^{3+}$ (33%^[8]). Present-day high-power Yb-based laser systems have used this advantage to achieve pulse energies higher than 50 J^[9] and 100 J^[10] within pulse durations of 100 fs and 10 ns, respectively. Despite the reduced heat load within $\text{Yb}^{3+}$ -doped materials, significant detrimental effects can still occur due to the pump-induced thermal profile. The influence of strong thermally induced^[5] wavefront aberrations – in conjunction with electronic contributions^[11] – may heavily distort^[12] the amplified beam profile upon propagation. Additionally, the spatially varying depolarization of the amplified seed beam due to thermal stress^[5] induced by the thermal gradient in a multi-hundred-joule pumped active material can directly lead to energy loss and possible spatial profile deformations after interacting with polarization-sensitive optical components within the laser system. If not properly characterized and controlled, the thermal profile within a strongly pumped active material can not only limit the maximum achievable energy and final focusability of the laser pulse, but ultimately, in cases of high thermal stress, result in permanent damage to the active material.

A measurement technique that is capable of resolving the complete spatio-temporal thermal profile of the pumped active materials is challenging, due to the high emissivity of these materials. Measurements^[5] utilizing thermal infrared imaging cameras, for example, are only able to access the surface temperature profiles with limited temporal resolution, due to the camera’s long integration time compared to the typical pump pulse durations utilized with $\text{Yb}^{3+}$ -doped active materials^[6]. Interferometric temperature measurements or measurements of temperature-dependent absorption^[13], on the other hand, only provide information about the temperature averaged over the thickness of the material. Recently, a novel scanning method^[14] that is capable of measuring the temperature inside the active material has been reported. The applicability of this method to joule-class laser amplifiers is currently limited, however, due to the large active material radius in conjunction with the typically low amplifier repetition rates, as well as the vast material dataset required to calibrate the fitting function. Therefore, a characterization of the temporally resolved 3D thermal profiles of active materials under complex pumping configurations, such as with the 3D multi-spot pump setup of the POLARIS^[9] laser system, cannot be adequately realized with these methods alone.

However, with extensive knowledge of the material parameters, including the doping-dependent thermal properties of the materials and the inversion-dependent absorption of the pump pulse, a highly accurate numerical model can be constructed and verified to provide access to the complete spatio-temporal thermal profiles. Such thermal simulations are a necessary tool to access the temperature profile within the materials, which may strongly differ from the surface temperatures. A pump profile that is optimized solely according to the surface temperature distribution may produce high thermal gradients elsewhere in the active material, leading to significant wavefront aberrations and permanent material damage from the thermally induced stress.

In this paper we describe the temporally and spatially resolved temperature study of Yb:YAG, $\text{Yb:CaF}_{2}$ and Yb:fluorophosphate glass^[15] (Yb:FP15), which are commonly used in diode-pumped high-power laser systems such as the POLARIS laser system at the Friedrich-Schiller-University and Helmholtz-Institute Jena in Germany. A simple pump geometry with a homogeneous, square-shaped pump pulse together with a thermal camera was used as a measurement setup to benchmark the detailed temperature simulations, which showed excellent agreement with the measurements. The calibrated measurement method was then applied to the 3D pumping configuration of a joule-class Yb:FP15-based amplifier operating in the POLARIS laser system. The individually measured surface temperature profiles of each pump pulse on the front and back sides of the active material could be combined via a complex simulation to enable access to the 3D spatio-temporal thermal profiles.

2 Thermal profile simulation

2.1 Heat transfer and active material parameters

Numerical simulations of the spatio-temporal behavior and magnitude of the temperature profile throughout the pumped material can be accomplished through the use of finite element analysis software. Here, COMSOL (Version 5.2, Sweden) was employed to construct a 3D model of the pumped active material and solve the time-dependent heat transfer equation

(1) $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D70C}C_{p}\frac{\unicode[STIX]{x2202}T(x,y,z,t)}{\unicode[STIX]{x2202}t}-K_{\text{th}}\unicode[STIX]{x1D6FB}^{2}T(x,y,z,t)\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D702}_{h}\unicode[STIX]{x1D6FC}I(x,y,t)A(z,t),\end{eqnarray}$$

which predicts the flow of heat through a material via conduction^[5], based on the given pump conditions.

The individual components of Equation (1) grant an understanding into how the material parameters contribute to the thermal profile $T(x,y,z,t)$ of the material. The specific heat capacity $C_{p}\,[\frac{\text{J}}{\text{kg}\,\cdot \,\text{K}}]$ , which can be calculated using the Debye model^[16] for a given doping concentration, along with the density $\unicode[STIX]{x1D70C}\,[\frac{\text{kg}}{\text{m}^{3}}]$ affects the temperature variation in the pulsed regime. The magnitude of the temperature gradient in the material scales with the thermal conductivity $K_{\text{th}}\,[\frac{\text{W}}{\text{m}\,\cdot \,\text{K}}]$ , which can be determined from Gaumé’s model as^[17]

(2) $$\begin{eqnarray}K_{\text{th}}=B\cdot \sqrt{\frac{K_{\text{th},0}}{d}}\cdot \arctan \left(\frac{\sqrt{K_{\text{th},0}\cdot d}}{B}\right),\end{eqnarray}$$

where $d$ is the doping concentration, $K_{\text{th},0}$ is the undoped thermal conductivity, and $B$ is an empirically determined^[17] fit parameter.

The term on the right-hand side of Equation (1) represents the absorbed power density of the heat source within the material. Here, the heat source is the pump laser with intensity $I(x,y,t)$ , which exhibits a homogeneous spatial profile and a square-like periodic temporal profile. The strength of the absorbed power density is also determined by the absorption $\unicode[STIX]{x1D6FC}\,[\frac{1}{\text{m}}]$ of the material, which is dependent on the dopant concentration, and the percentage $\unicode[STIX]{x1D702}_{h}$ of energy transferred to heat through the quantum defect and other nonradiative transitions due to material impurities. The form of the pump laser depletion along the material’s length is given by the parameter $A(z,t)$ . The material parameters required for the thermal profile simulation of the considered active materials are given in Table 1.

2.2 Inversion-corrected pump depletion

The profile of the pump depletion $A(z,t)=I(z,t)/I(0,0)$ along the propagation direction $z$ was calculated numerically^[6] by iteratively determining the remaining pump intensity $I(z,t)$ and population inversion level $\unicode[STIX]{x1D6FD}(z,t)$ along the length of the active material throughout the pump pulse duration:

(3) $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}I(z,t)}{\unicode[STIX]{x2202}z}=-N_{\text{dot}}\cdot \unicode[STIX]{x1D70E}_{a}\cdot \left[1-\frac{\unicode[STIX]{x1D6FD}(z,t)}{\unicode[STIX]{x1D6FD}_{\text{eq}}}\right]\cdot I(z,t), & \displaystyle\end{eqnarray}$$

(4) $$\begin{eqnarray}\displaystyle & \displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FD}(z,t)}{\unicode[STIX]{x2202}t}=I(z,t)\cdot \frac{\unicode[STIX]{x1D706}\cdot \unicode[STIX]{x1D70E}_{a}}{h\cdot c\cdot \unicode[STIX]{x1D6FD}_{\text{eq}}}\cdot \left[1-\frac{\unicode[STIX]{x1D6FD}(z,t)}{\unicode[STIX]{x1D6FD}_{\text{eq}}}\right]-\frac{\unicode[STIX]{x1D6FD}_{\text{eq}}}{\unicode[STIX]{x1D70F}_{f}}. & \displaystyle\end{eqnarray}$$

Figure 1. Numerical calculation of the normalized pump intensity within a Yb:YAG crystal in comparison to the Lambert–Beer and saturated absorption models.

Table 1. Relevant optical and thermal properties of the considered active materials.

In Equations (3) and (4), $\unicode[STIX]{x1D70E}_{a}$ is the absorption cross-section, $N_{\text{dot}}$ is the dopant density, $\unicode[STIX]{x1D70F}_{f}$ is the fluorescence lifetime, and $\unicode[STIX]{x1D6FD}_{\text{eq}}$ represents the equilibrium inversion level, which is required to ‘bleach’ the material, such that the increase of the inversion induced by the pump is balanced with its decrease via emission. The influence of the nonzero inversion on the pump absorption is not included in the frequently utilized models of Lambert–Beer

(5) $$\begin{eqnarray}\frac{\unicode[STIX]{x2202}I(z)}{\unicode[STIX]{x2202}z}=-\unicode[STIX]{x1D6FC}I(z)\end{eqnarray}$$

and saturated absorption

(6) $$\begin{eqnarray}\frac{\unicode[STIX]{x2202}I(z)}{\unicode[STIX]{x2202}z}=-\frac{\unicode[STIX]{x1D6FC}}{1+\frac{I(z)}{I_{\text{sat}}}}I(z).\end{eqnarray}$$

Figure 1 displays the numerical calculation of the pump depletion, corrected for the nonzero inversion, for the case of Yb:YAG pumped near the saturation intensity $I_{\text{sat}}$ . The Lambert–Beer model was found to underestimate the remaining pump intensity along the 4.5-mm-thick active material by ${\leqslant}$ 12%, while the saturated absorption model overestimated the remaining pump intensity by ${\leqslant}$ 7%. By implementing a proper numerical calculation of the pump depletion in the active material, significant inaccuracies in the value of the absorbed power density in the thermal simulation can be avoided, the relevance of which increases for high pump energies and multiple pump sources.

3 Verification of the numerical simulation

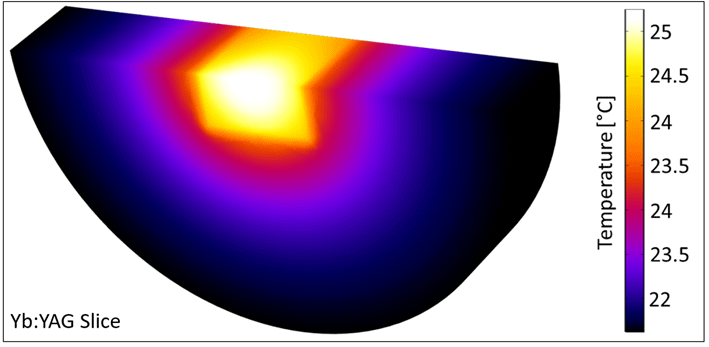
Figure 2. A slice through the pumped Yb:YAG model in COMSOL.

Figure 3. Pump profile (a) and thermal image (b) of the end-pumped and water-cooled $\text{Yb:CaF}_{2}$ .

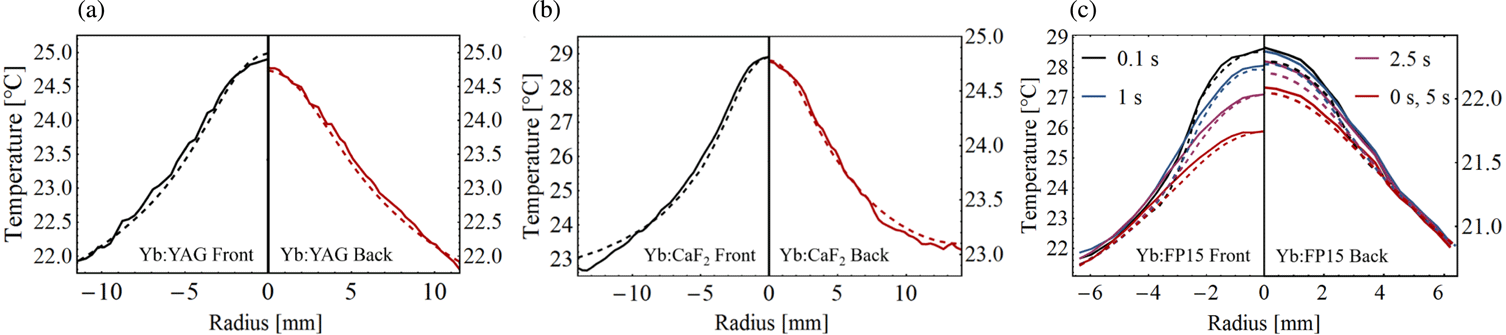
Figure 4. Comparison of measured (solid) and simulated (dashed) thermal profiles. The measured temperature profiles for (a) Yb:YAG and (b) $\text{Yb:CaF}_{2}$ on both the front and back surfaces were compared to the simulated temperature profiles averaged over the pump cycle. (c) The front and back Yb:FP15 profiles are displayed for times 0 (directly before the 1.4 ms pump pulse), 0.1, 1, 2.5, and 5 s within the pump cycle (repetition rate 0.2 Hz).

An example of the simulated Yb:YAG model is displayed in Figure 2. The results of the thermal simulation – including the doping-dependent active material parameters and the inversion-corrected pump depletion – reveal the transformation of the temperature profile throughout the material, but must be checked for validity using thermal measurements and well-defined pumping conditions.

For a controlled investigation of the temperature changes within the pumped active materials, a homogenized 6.8 kW laser diode source was constructed as the pump laser. Each active material was end-pumped with an empirically determined repetition rate according to the ability of the material to diffuse heat (Yb:YAG – 2 Hz, $\text{Yb:CaF}_{2}$ – 4 Hz, Yb:FP15 – 0.2 Hz). The pump pulse duration was chosen according to the fluorescence lifetime: Yb:YAG – 0.95 ms^[6], $\text{Yb:CaF}_{2}$ – 1.9 ms^[6], Yb:FP15 – 1.4 ms^[15]. Thermal measurements were taken after the materials reached a steady-state (‘thermalized’) regime, in which the average temperature no longer increased with the number of pump cycles.

The numerical model was tested for accuracy using the thermal IR camera FLIR P620^[21], which has $640\times 480$ pixels and a thermal sensitivity of 0.04 K. The camera utilizes a microbolometer array with a temperature-dependent electrical resistance. By imaging IR radiation in the range $8{-}12~\unicode[STIX]{x03BC}\text{m}$ onto the array, a local change in the resistance occurs due to the absorbed radiation, from which the local temperature can be determined. The thermal camera can be calibrated using the emissivity value $\unicode[STIX]{x1D700}$ of the object to be measured, which was determined by placing black tape onto the water-cooled mount with a known temperature value of $20.5\,^{\circ }\text{C}$ and adjusting the emissivity setting on the thermal camera until the measured temperature matched the temperature of the mount. Additional calibration measurements, in which the temperature of $\text{Yb:CaF}_{2}$ and Yb:FP15 was varied between $20\,^{\circ }\text{C}$ and $50\,^{\circ }\text{C}$ and simultaneously measured with a temperature sensor, resulted in an emissivity value of $\unicode[STIX]{x1D700}=0.94$ for both materials and both calibration methods. Due to the high emissivity value, only radiation from a very small depth through the material can be detected by the thermal camera. Hence, only the surface temperature could be measured. The pump profile and a thermal image of the pumped $\text{Yb:CaF}_{2}$ with the FLIR P620 camera are displayed in Figure 3.

The thermal camera additionally provides a minimum time interval of 30 ms between two consecutive measurements, which enables the measurement of the surface temperature profile at various times throughout the pump cycle. Thus, the temporally and spatially resolved temperature measurements are well suited for verifying the thermal simulations. Comparisons of the thermal measurements and simulations are displayed in Figure 4.

The time-resolved detection of the temperature profile during the cooling phase of the pump cycle was possible for Yb:FP15 due to the low thermal conductivity, and consequently, the long thermal diffusion time^[12], that leads to a quasi-static state during the integration time of the thermal camera. For Yb:YAG (Figure 4(a)) and $\text{Yb:CaF}_{2}$ (Figure 4(b)), the simulated (dashed) front (black) and back (red) temperature profiles averaged over the pump cycle were compared to the measured (solid) profiles, with a maximum discrepancy between simulation and measurement of less than $0.3\,^{\circ }\text{C}$ . The maximum temperature difference between the measured and simulated temperature profiles of the pumped Yb:FP15 (Figure 4(c)) material throughout the 5 s pump cycle was determined to be below $0.2\,^{\circ }\text{C}$ . The modeling and validation principles described here are not only applicable to the comprehensive characterization of thermal effects – such as the inhomogeneous thermal contribution to pump-induced wavefront aberrations^[12] – in isolated setups, but can also be utilized to access the crucial 3D spatio-temporal thermal profile of a pumped active material in a high-energy amplifier under complex pumping configurations.

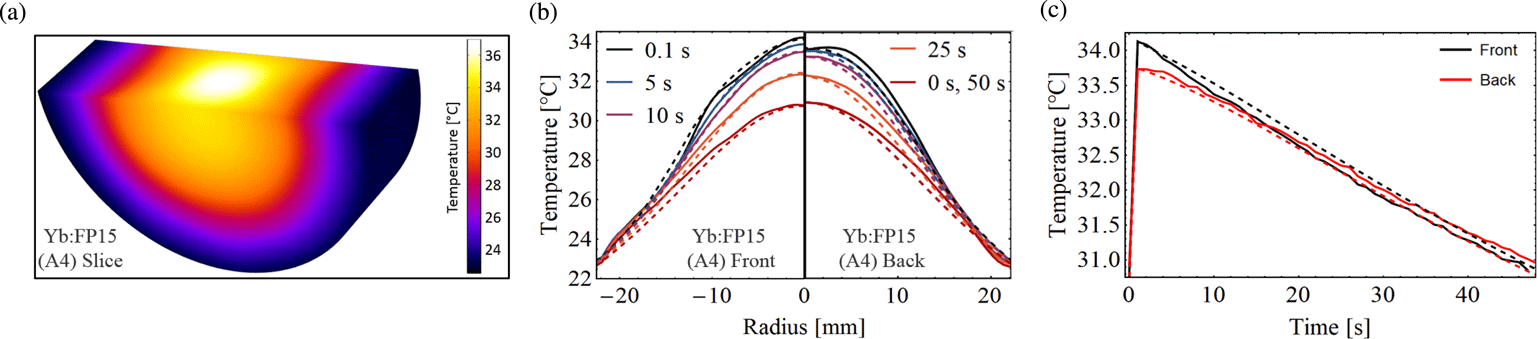
Figure 5. Schematic of the 3D pumping configuration of the Yb:FP15-based (perimeter in blue) A4 multi-pass amplifier at POLARIS with thermal images of an example of a single pump spot (top left) and the full pump profile (top right).

Figure 6. Comparison of measured (solid) and simulated (dashed) thermal profiles of the pumped and thermalized Yb:FP15 within the A4 amplifier. A slice through the pumped Yb:FP15 model in COMSOL is shown in (a). The front and back Yb:FP15 profiles are displayed in (b) for times 0 (directly before the 2.7 ms pump pulse), 0.1, 5, 10, 25, and 50 s within the pump cycle (repetition rate 0.02 Hz). The temperature on the front and back centers of the Yb:FP15 material is plotted in (c) throughout the pump cycle.

4 3D spatio-temporal thermal profile characterization

The pump energies employed in joule-class laser amplifiers lead to the formation of strong thermal gradients within the active material that can significantly impact the quality of the amplified seed beam and limit the final fluence and intensity of the laser system. Such thermal gradients can be directly transferred to the phase of the amplified seed beam and result in wavefront aberrations, and thus a deterioration of the spatial profile during propagation within the multi-pass amplifier. Another consequence of a strong thermal gradient is the buildup of thermal stress within the pumped active material, in which spatially varying stress-induced birefringence causes the inhomogeneous depolarization of the amplified seed beam, leading to energy loss as well as spatial deformations after interactions with polarization optics. Furthermore, the inhomogeneous thermal profile can directly influence the local absorption and emission cross-sections, resulting in spatial variations not only for the amplified spectrum, but also the transverse gain profile. For example, as the emission cross-section decreases in regions of higher temperature, a strong thermal gradient within the pumped active material can deform the spatial profile of the amplified seed beam via a reshaping of the gain profile^[6]. Additionally, the spatially inhomogeneous spectrum of the amplified pulse directly leads to a distortion of the spatio-temporal profile after compression, with different pulse durations along the beam radius. Consequently, as these effects lead to lower final energies, a reduced focusability of the laser system, and in the worst case, permanent material damage via thermal stress, the complete 3D thermal profile within the pumped active material must be accessed and controlled, if possible.

For this purpose, the verified model was utilized to characterize the 3D spatio-temporal thermal profile of the pumped Yb:FP15 in the joule-class ‘A4’ multi-pass amplifier currently operating in the POLARIS^[9] laser system. Within the A4 amplifier, a complex 3D pumping configuration^[22], a schematic of which is displayed in Figure 5, is employed, which contains 40 2.5 kW laser diode modules with an average 6.2 mm $\times$ 2.7 mm $1/e^{2}$ beam radius delivering a total pump energy of over 250 J within a 17.5 mm $1/e^{2}$ beam radius to the water-cooled Yb:FP15 active material that is utilized to amplify the seed beam up to 7 J in a nine-pass configuration. The position of each of the pump spots is individually tailored by a specially developed routine^[23] to achieve the desired pump distribution with regards to the spatial gain profile.

To adequately model the 3D pumping configuration, the front and back beam profiles of each of the 40 pump spots as well as the complete front and back pumping profiles were captured by the thermal infrared imaging camera, which was triggered and synchronized with each pump pulse. Due to the very low thermal conductivity and high emissivity of Yb:FP15, the surface thermal profiles generated by the individual beams can be assumed to be quasi-static within the integration time of the thermal camera. Thus, the individual thermal profiles could be directly correlated to the beam profiles, which were then best characterized by an elliptical Gaussian-like spatial distribution according to their energy $E_{i}$ , central positions $x_{c}$ and $y_{c}$ , orthogonal $1/e^{2}$ beam radii $\unicode[STIX]{x1D714}_{\max }$ and $\unicode[STIX]{x1D714}_{\min }$ , rotation angle $\unicode[STIX]{x1D703}$ with respect to the $xy$ -frame, incidence angles $\unicode[STIX]{x1D719}_{x}$ and $\unicode[STIX]{x1D719}_{y}$ , and pump pulse duration $\unicode[STIX]{x1D70F}_{\text{pump}}$ :

(7) $$\begin{eqnarray}\displaystyle & & \displaystyle I(x,y,z,t)\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{i=1}^{40}E_{i}\cdot \exp \left\{-\left[\left(\frac{\cos \unicode[STIX]{x1D703}_{i}\cdot X_{i}+\sin \unicode[STIX]{x1D703}_{i}\cdot Y_{i}}{\unicode[STIX]{x1D714}_{\max ,i}}\right)^{2}\right.\right.\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\left.\left.\left(\frac{-\sin \unicode[STIX]{x1D703}_{i}\cdot X_{i}+\cos \unicode[STIX]{x1D703}_{i}\cdot Y_{i}}{\unicode[STIX]{x1D714}_{\min ,i}}\right)^{2}\right]\right\}\nonumber\\ \displaystyle & & \displaystyle \qquad \cdot \,A_{i}(z)\cdot \text{rect}\left(\frac{t}{\unicode[STIX]{x1D70F}_{\text{pump}}}\right),\end{eqnarray}$$

where $X_{i}=x-(x_{c}-z\cdot \text{tan}\unicode[STIX]{x1D719}_{x})$ , $Y_{i}=y-(y_{c}-z\cdot \text{tan}\unicode[STIX]{x1D719}_{y})$ .

Figure 7. Comparison of the measured (solid) and simulated (dashed) front, back, and middle thermal profiles of the pumped Yb:FP15 within the A4 amplifier.

The total A4 pump profile $I(x,y,z,t)$ , as seen in Equation (7), including the numerically calculated pump depletion profile $A_{i}(z)$ , was inserted into the thermal model along with the doping-dependent thermal properties of Yb:FP15. The results of the numerical simulation were compared to surface temperature measurements utilizing the thermal infrared imaging camera of both the front and back sides of the thermalized Yb:FP15 material, which was pumped by the full pump profile (Figure 5, top right). As seen in Figure 6, the thermal model and measurements are in good agreement, with an RMS (root mean square) temperature difference of less than 1.5% ( $0.5\,^{\circ }\text{C}$ ) of the maximum temperature.

Additionally, the spatio-temporal thermal model of the Yb:FP15 material in the A4 amplifier reveals details about the thermal profile inside the laser medium that are inaccessible from the surface thermal measurements. The results displayed in Figure 7 show that the amplitude of the thermal gradient, defined here as the temperature difference $\unicode[STIX]{x0394}T$ between the center (radius $=$ 0 mm) and the edge (radius $=$   $\pm$ 22.5 mm) of the pumped and thermalized active material, is 24% higher in the middle than on the measurable (front and back) surfaces. The consequences of this strong inner thermal gradient are not only higher thermal stresses than anticipated based on the surface pump fluence, but also stronger wavefront aberrations that add up with each of the nine passes in the joule-class amplifier.

A comparison of the thermal profile of Yb:FP15 glass with that of the two crystals in Section 3, Yb:YAG and $\text{Yb:CaF}_{2}$ , under the same pumping conditions within the A4 amplifier would result in an overall stronger thermal gradient and higher peak temperature for Yb:FP15, as the thermal conductivity – seen in Table 1 – is nearly an order of magnitude lower than for the cases of Yb:YAG and $\text{Yb:CaF}_{2}$ . The crystals would allow for a higher repetition rate of the amplifier; however, at the cost of narrower emission cross-sections and an increase in the impact of the thermal contributions to the spatial degradation of the amplified seed pulse, due to the significantly higher thermo-optic coefficients^[12].

The information provided by this benchmarked 3D spatio-temporal thermal profile model can be employed for further investigations of spatially and temporally varying wavefront aberrations, stress-induced depolarization, and local modifications in the absorption and emission properties in the context of a joule-class multi-pass $\text{Yb}^{3+}$ -doped laser amplifier.

5 Conclusion

An optimization of the final multi-pass amplifier stages in a high-peak-power laser system can directly lead to an increase in the pulse energy and an improvement in the beam focusability, thereby increasing the achievable intensity and allowing access to new developments in relativistic laser plasma physics. However, the high pump energies required to achieve a sufficient gain result in strong thermally induced changes in a pumped active material’s refractive index profile, along with thermal expansion and stress, which can cause permanent damage to the active material. In addition, the large beam diameters and long propagation distances present within joule-class multi-pass amplifiers increase the importance of managing the pump-induced refractive index changes, which can otherwise significantly deteriorate the amplified seed beam’s spatial profile. To further investigate and possibly mitigate these effects in a joule-class amplifier, the knowledge from a 3D spatio-temporal thermal profile characterization of the pumped active material, currently only accessible via benchmarked thermal simulations, is crucial.

In this investigation, multiple spatio-temporal numerical simulations were tested for accuracy against thermal measurements of end-pumped and water-cooled Yb:YAG, $\text{Yb:CaF}_{2}$ and Yb:FP15. The realized pump source was a homogenized square-shaped 6.8 kW laser diode module, which was utilized to pump the active materials with pulse durations from 0.9 to 2 ms and repetition rates from 0.2 to 4 Hz.

The COMSOL-based spatio-temporal thermal profile models were constructed using knowledge of the dopant-dependent thermal properties of the considered active materials. A numerical calculation of the pump depletion throughout the material was utilized and compared to the Lambert–Beer and saturated absorption approaches, which neglect the inversion within the pumped active materials. The thermal simulations agreed with surface measurements utilizing a thermal infrared imaging camera for Yb:YAG and $\text{Yb:CaF}_{2}$ within $0.3\,^{\circ }\text{C}$ and for Yb:FP15 within $0.2\,^{\circ }\text{C}$ throughout the pump cycle.

The model was then applied to a joule-class $\text{Yb}^{3+}$ -based amplifier in the POLARIS laser system currently operating with 40 pump modules in a complex 3D pumping configuration. Each pump beam was characterized according to its energy, spatial profile, position and incidence angle, and recreated within the numerical simulation. The results of the thermal model deviated from front and back surface thermal measurements of the pumped active material with an RMS value of less than $0.5\,^{\circ }\text{C}$ throughout the pump cycle. Utilizing the detailed and benchmarked thermal simulation, a localized hot region – thus far undetectable by the thermal infrared imaging camera due to the high emissivity of the material – was revealed in the center of the pumped active material. With this complete spatio-temporal thermal profile, such potentially dangerous thermal features can be discovered and controlled to prevent material damage and lessen the extent of spatial deformations that may severely limit the final fluence of joule-class laser systems.