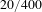1 Introduction
High power fiber lasers have drawn great attention since they provide many great advantages such as high output efficiency, good power handling and beam quality and better thermal management[Reference Richardson, Nilsson and Clarkson1–Reference Jauregui, Limpert and Tünnermann3]. The output power of fiber lasers has been greatly scaled up due to renewal of the pump source and the dual cladding fibers. Further increasing the output power of fiber lasers and amplifier is limited by several factors including pump brightness, nonlinear effects, thermal lensing and the thermally induced mode instability (TMI)[Reference Zervas and Codemard4]. Among these effects, the TMI is believed to be the major bottle neck to the power scaling of fiber laser source with near diffraction limited beam quality.
The TMI effect is that the signal power fluctuates between the fundamental mode (FM) and the first few higher-order modes (HOMs) when the average signal power reaches a certain threshold[Reference Eidam, Wirth, Jauregui, Stutzki, Jansen, Otto, Schmidt, Schreiber, Limpert and Tünnermann5]. The main physical mechanism for the TMI is believed to be the stimulated thermal Rayleigh scattering, which is induced by the quantum defect heating of the active fiber[Reference Jauregui, Eidam, Otto, Stutzki, Jansen, Limpert and Tunnermann6–Reference Dong9]. Several numerical models based on the beam propagation method (BPM)[Reference Otto, Jauregui, Eidam, Stutzki, Jansen, Limpert and Tünnermann10–Reference Smith and Smith13] and coupled-mode theory[Reference Hansen, Alkeskjold, Broeng and Lægsgaard14, Reference Hansen and Lægsgaard15] have been demonstrated to explain the TMI effect. These models are suitable for the situation of the uncoiled fiber. For the TMI in the coiled fiber, A. V. Smith and J. J. Smith proposed the BPM model which considers a preset mode loss[Reference Smith and Smith16]. Tao et al. proposed a semi-analytical model[Reference Tao, Su, Ma, Wang and Zhou17] based on the mode bending loss calculated by the Marcuse’s formula[Reference Marcuse18]. However, these models do not consider the thermally induced mode bending loss decrease[Reference Charles, Shatrovoy, Fan and Taunay19, Reference Kong, Leng, Zhou and Jiang20]. Therefore, a more general model that considers the thermally induced mode bending loss decrease and the TMI effect in the coiled fiber is needed.
In our previous work, we demonstrated the experimental investigation of the thermally induced core laser leakage (TICLL) effect in the co-pumped high power fiber amplifier that the output power starts to decrease and the core signal power begins to couple into the inner cladding when a certain pump power threshold is reached[Reference Kong, Huang, Gu, Leng, Guo, Zhou, Xu and Jiang21, Reference Kong, Li, Leng, Wang, Zhou, Xu, Chen and Jiang22]. However, only considering the thermally induced mode bending loss decrease will not lead to the output power decrease[Reference Kong, Leng, Zhou and Jiang20]. We believe that the thermally induced mode bending loss decrease and the TMI effect are the two key factors which lead to the TICLL effect. In order to combine these two effects and explain the physical process of the TICLL, thus in this paper, we established an improved coupled-mode equation based on the local mode theory. This paper consists of three parts. The first part is the establishment of the theoretical model. The second part is the simulation of the TICLL effect in the co-pumped step-index
![]() $20/400$
fiber amplifier. The third part discusses the mitigating strategy of the TICLL effect via the counter-pumping scheme.
$20/400$
fiber amplifier. The third part discusses the mitigating strategy of the TICLL effect via the counter-pumping scheme.
2 Coupled-mode model
We consider the signal field in the scalar approximation and the electric field could be written as
where
![]() $\overset{\rightharpoonup }{u}$
stands for the unit polarization vector. Typically, the mode coupling only happens between the FM and the first HOM[Reference Hansen and Lægsgaard15], and thus in this paper we only consider these two modes:
$\overset{\rightharpoonup }{u}$
stands for the unit polarization vector. Typically, the mode coupling only happens between the FM and the first HOM[Reference Hansen and Lægsgaard15], and thus in this paper we only consider these two modes:
where
![]() $A_{1}$
and
$A_{1}$
and
![]() $A_{2}$
are the mode amplitudes with normalized mode fields
$A_{2}$
are the mode amplitudes with normalized mode fields
![]() $\unicode[STIX]{x1D711}_{1}$
,
$\unicode[STIX]{x1D711}_{1}$
,
![]() $\unicode[STIX]{x1D711}_{2}$
and the propagation constants
$\unicode[STIX]{x1D711}_{2}$
and the propagation constants
![]() $\unicode[STIX]{x1D6FD}_{1}$
,
$\unicode[STIX]{x1D6FD}_{1}$
,
![]() $\unicode[STIX]{x1D6FD}_{2}$
.
$\unicode[STIX]{x1D6FD}_{2}$
.
![]() $w_{1}$
and
$w_{1}$
and
![]() $w_{2}$
represent the frequency for FM and HOM, while
$w_{2}$
represent the frequency for FM and HOM, while
![]() $\unicode[STIX]{x1D6FC}_{1}$
and
$\unicode[STIX]{x1D6FC}_{1}$
and
![]() $\unicode[STIX]{x1D6FC}_{2}$
are the FM bending loss and HOM bending loss, respectively. The pertinent wave equation for the isotropic medium derived from Maxwell’s equation is given by
$\unicode[STIX]{x1D6FC}_{2}$
are the FM bending loss and HOM bending loss, respectively. The pertinent wave equation for the isotropic medium derived from Maxwell’s equation is given by
where
![]() $n$
is the refractive index of the fiber material, which is now a function of space and time attributed to the thermal effect.
$n$
is the refractive index of the fiber material, which is now a function of space and time attributed to the thermal effect.
![]() $c$
is the light propagation speed in vacuum and
$c$
is the light propagation speed in vacuum and
![]() $\unicode[STIX]{x1D707}_{0}$
is the vacuum permeability.
$\unicode[STIX]{x1D707}_{0}$
is the vacuum permeability.
![]() $\overset{\rightharpoonup }{P}$
stands for the laser gain induced polarization. We assume the field to be
$\overset{\rightharpoonup }{P}$
stands for the laser gain induced polarization. We assume the field to be
![]() $X$
direction polarized for convenience and substitute the signal field into the wave equation. The first term on the left-hand side (LHS) could be written as
$X$
direction polarized for convenience and substitute the signal field into the wave equation. The first term on the left-hand side (LHS) could be written as
 $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6FB}^{2}E_{s}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{2}[A_{1}\unicode[STIX]{x1D6FB}_{t}^{2}\unicode[STIX]{x1D711}_{1}e^{i(\unicode[STIX]{x1D6FD}_{1}z-w_{1}t)-\unicode[STIX]{x1D6FC}_{1}z}+A_{2}\unicode[STIX]{x1D6FB}_{t}^{2}\unicode[STIX]{x1D711}_{2}e^{i(\unicode[STIX]{x1D6FD}_{2}z-w_{2}t)-\unicode[STIX]{x1D6FC}_{2}z}]\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{1}{2}\left[\vphantom{\left(\frac{\unicode[STIX]{x2202}A_{1}}{\unicode[STIX]{x2202}z}\unicode[STIX]{x1D711}_{1}+A_{1}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{1}}{\unicode[STIX]{x2202}z}\right)}(i\unicode[STIX]{x1D6FD}_{1}-\unicode[STIX]{x1D6FC}_{1})^{2}A_{1}\unicode[STIX]{x1D711}_{1}+2(i\unicode[STIX]{x1D6FD}_{1}-\unicode[STIX]{x1D6FC}_{1})\right.\nonumber\\ \displaystyle & & \displaystyle \qquad \times \left.\left(\frac{\unicode[STIX]{x2202}A_{1}}{\unicode[STIX]{x2202}z}\unicode[STIX]{x1D711}_{1}+A_{1}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{1}}{\unicode[STIX]{x2202}z}\right)\right]e^{i(\unicode[STIX]{x1D6FD}_{1}z-w_{1}t)-\unicode[STIX]{x1D6FC}_{1}z}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\frac{1}{2}\left[\vphantom{\left(\frac{\unicode[STIX]{x2202}A_{1}}{\unicode[STIX]{x2202}z}\unicode[STIX]{x1D711}_{1}+A_{1}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{1}}{\unicode[STIX]{x2202}z}\right)}(i\unicode[STIX]{x1D6FD}_{2}-\unicode[STIX]{x1D6FC}_{2})^{2}A_{1}\unicode[STIX]{x1D711}_{1}+2(i\unicode[STIX]{x1D6FD}_{2}-\unicode[STIX]{x1D6FC}_{2})\right.\nonumber\\ \displaystyle & & \displaystyle \qquad \times \left.\left(\frac{\unicode[STIX]{x2202}A_{2}}{\unicode[STIX]{x2202}z}\unicode[STIX]{x1D711}_{2}+A_{2}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{2}}{\unicode[STIX]{x2202}z}\right)\right]e^{i(\unicode[STIX]{x1D6FD}_{2}z-w_{2}t)-\unicode[STIX]{x1D6FC}_{2}z}+\text{c.c.},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6FB}^{2}E_{s}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{2}[A_{1}\unicode[STIX]{x1D6FB}_{t}^{2}\unicode[STIX]{x1D711}_{1}e^{i(\unicode[STIX]{x1D6FD}_{1}z-w_{1}t)-\unicode[STIX]{x1D6FC}_{1}z}+A_{2}\unicode[STIX]{x1D6FB}_{t}^{2}\unicode[STIX]{x1D711}_{2}e^{i(\unicode[STIX]{x1D6FD}_{2}z-w_{2}t)-\unicode[STIX]{x1D6FC}_{2}z}]\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{1}{2}\left[\vphantom{\left(\frac{\unicode[STIX]{x2202}A_{1}}{\unicode[STIX]{x2202}z}\unicode[STIX]{x1D711}_{1}+A_{1}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{1}}{\unicode[STIX]{x2202}z}\right)}(i\unicode[STIX]{x1D6FD}_{1}-\unicode[STIX]{x1D6FC}_{1})^{2}A_{1}\unicode[STIX]{x1D711}_{1}+2(i\unicode[STIX]{x1D6FD}_{1}-\unicode[STIX]{x1D6FC}_{1})\right.\nonumber\\ \displaystyle & & \displaystyle \qquad \times \left.\left(\frac{\unicode[STIX]{x2202}A_{1}}{\unicode[STIX]{x2202}z}\unicode[STIX]{x1D711}_{1}+A_{1}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{1}}{\unicode[STIX]{x2202}z}\right)\right]e^{i(\unicode[STIX]{x1D6FD}_{1}z-w_{1}t)-\unicode[STIX]{x1D6FC}_{1}z}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\frac{1}{2}\left[\vphantom{\left(\frac{\unicode[STIX]{x2202}A_{1}}{\unicode[STIX]{x2202}z}\unicode[STIX]{x1D711}_{1}+A_{1}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{1}}{\unicode[STIX]{x2202}z}\right)}(i\unicode[STIX]{x1D6FD}_{2}-\unicode[STIX]{x1D6FC}_{2})^{2}A_{1}\unicode[STIX]{x1D711}_{1}+2(i\unicode[STIX]{x1D6FD}_{2}-\unicode[STIX]{x1D6FC}_{2})\right.\nonumber\\ \displaystyle & & \displaystyle \qquad \times \left.\left(\frac{\unicode[STIX]{x2202}A_{2}}{\unicode[STIX]{x2202}z}\unicode[STIX]{x1D711}_{2}+A_{2}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{2}}{\unicode[STIX]{x2202}z}\right)\right]e^{i(\unicode[STIX]{x1D6FD}_{2}z-w_{2}t)-\unicode[STIX]{x1D6FC}_{2}z}+\text{c.c.},\end{eqnarray}$$
where only the first order term along the
![]() $Z$
direction is considered. The second term on the LHS is zero if it is retained in the first order:
$Z$
direction is considered. The second term on the LHS is zero if it is retained in the first order:
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FB}\left(\frac{1}{n^{2}}\overset{\rightharpoonup }{E}\cdot \unicode[STIX]{x1D6FB}n^{2}\right) & = & \displaystyle \overset{\rightharpoonup }{x}\left[\frac{1}{n}\frac{\unicode[STIX]{x2202}E_{s}}{\unicode[STIX]{x2202}x}\frac{\unicode[STIX]{x2202}n}{\unicode[STIX]{x2202}x}+\frac{E_{s}}{n^{2}}\left(\frac{\unicode[STIX]{x2202}n}{\unicode[STIX]{x2202}x}\right)^{2}\right.\nonumber\\ \displaystyle & & \displaystyle +\left.\frac{E_{s}}{n^{2}}\frac{\unicode[STIX]{x2202}^{2}n}{\unicode[STIX]{x2202}x^{2}}\right]=0.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FB}\left(\frac{1}{n^{2}}\overset{\rightharpoonup }{E}\cdot \unicode[STIX]{x1D6FB}n^{2}\right) & = & \displaystyle \overset{\rightharpoonup }{x}\left[\frac{1}{n}\frac{\unicode[STIX]{x2202}E_{s}}{\unicode[STIX]{x2202}x}\frac{\unicode[STIX]{x2202}n}{\unicode[STIX]{x2202}x}+\frac{E_{s}}{n^{2}}\left(\frac{\unicode[STIX]{x2202}n}{\unicode[STIX]{x2202}x}\right)^{2}\right.\nonumber\\ \displaystyle & & \displaystyle +\left.\frac{E_{s}}{n^{2}}\frac{\unicode[STIX]{x2202}^{2}n}{\unicode[STIX]{x2202}x^{2}}\right]=0.\end{eqnarray}$$
According to the approximation in Ref. [Reference Naderi, Dajani, Madden and Robin23], the third term on the LHS and the term on the right-hand side follow
 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{1}{c^{2}}\frac{\unicode[STIX]{x2202}^{2}[n^{2}(r,t)\overset{\rightharpoonup }{E}]}{\unicode[STIX]{x2202}t^{2}}\nonumber\\ \displaystyle & & \displaystyle \quad =-\overset{\rightharpoonup }{x}\frac{1}{2}\left[\frac{n^{2}w_{1}^{2}}{c^{2}}A_{1}\unicode[STIX]{x1D711}_{1}e^{i(\unicode[STIX]{x1D6FD}_{1}z-w_{1}t)-\unicode[STIX]{x1D6FC}_{1}z}\right.\nonumber\\ \displaystyle & & \displaystyle \qquad +\left.\frac{n^{2}w_{2}^{2}}{c^{2}}A_{2}\unicode[STIX]{x1D711}_{2}e^{i(\unicode[STIX]{x1D6FD}_{2}z-w_{2}t)-\unicode[STIX]{x1D6FC}_{2}z}+\text{c.c.}\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{1}{c^{2}}\frac{\unicode[STIX]{x2202}^{2}[n^{2}(r,t)\overset{\rightharpoonup }{E}]}{\unicode[STIX]{x2202}t^{2}}\nonumber\\ \displaystyle & & \displaystyle \quad =-\overset{\rightharpoonup }{x}\frac{1}{2}\left[\frac{n^{2}w_{1}^{2}}{c^{2}}A_{1}\unicode[STIX]{x1D711}_{1}e^{i(\unicode[STIX]{x1D6FD}_{1}z-w_{1}t)-\unicode[STIX]{x1D6FC}_{1}z}\right.\nonumber\\ \displaystyle & & \displaystyle \qquad +\left.\frac{n^{2}w_{2}^{2}}{c^{2}}A_{2}\unicode[STIX]{x1D711}_{2}e^{i(\unicode[STIX]{x1D6FD}_{2}z-w_{2}t)-\unicode[STIX]{x1D6FC}_{2}z}+\text{c.c.}\right],\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D707}_{0}\frac{\unicode[STIX]{x2202}^{2}\overset{\rightharpoonup }{P}}{\unicode[STIX]{x2202}t^{2}}\nonumber\\ \displaystyle & & \displaystyle \quad =\overset{\rightharpoonup }{x}\frac{2in_{0}}{c}\left(\frac{\unicode[STIX]{x1D70E}_{s}^{e}N_{2}-\unicode[STIX]{x1D70E}_{s}^{a}N_{1}}{2}\right)\times \left[\frac{1}{2}w_{1}A_{1}\unicode[STIX]{x1D711}_{1}e^{i(\unicode[STIX]{x1D6FD}_{1}z-w_{1}t)-\unicode[STIX]{x1D6FC}_{1}z}\right.\nonumber\\ \displaystyle & & \displaystyle \qquad +\left.\frac{1}{2}w_{2}A_{2}\unicode[STIX]{x1D711}_{2}e^{i(\unicode[STIX]{x1D6FD}_{2}z-w_{2}t)-\unicode[STIX]{x1D6FC}_{2}z}+\text{c.c.}\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D707}_{0}\frac{\unicode[STIX]{x2202}^{2}\overset{\rightharpoonup }{P}}{\unicode[STIX]{x2202}t^{2}}\nonumber\\ \displaystyle & & \displaystyle \quad =\overset{\rightharpoonup }{x}\frac{2in_{0}}{c}\left(\frac{\unicode[STIX]{x1D70E}_{s}^{e}N_{2}-\unicode[STIX]{x1D70E}_{s}^{a}N_{1}}{2}\right)\times \left[\frac{1}{2}w_{1}A_{1}\unicode[STIX]{x1D711}_{1}e^{i(\unicode[STIX]{x1D6FD}_{1}z-w_{1}t)-\unicode[STIX]{x1D6FC}_{1}z}\right.\nonumber\\ \displaystyle & & \displaystyle \qquad +\left.\frac{1}{2}w_{2}A_{2}\unicode[STIX]{x1D711}_{2}e^{i(\unicode[STIX]{x1D6FD}_{2}z-w_{2}t)-\unicode[STIX]{x1D6FC}_{2}z}+\text{c.c.}\right],\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D70E}_{s}^{e}$
and
$\unicode[STIX]{x1D70E}_{s}^{e}$
and
![]() $\unicode[STIX]{x1D70E}_{s}^{a}$
are the emission/absorption cross section for the signal light.
$\unicode[STIX]{x1D70E}_{s}^{a}$
are the emission/absorption cross section for the signal light.
![]() $N_{2}$
and
$N_{2}$
and
![]() $N_{1}$
stand for the population of the upper state and ground state. The variation of the refractive index is on the order of milliseconds, and thus the terms such as
$N_{1}$
stand for the population of the upper state and ground state. The variation of the refractive index is on the order of milliseconds, and thus the terms such as
![]() $(\unicode[STIX]{x2202}^{2}n^{2}/\unicode[STIX]{x2202}t^{2})A_{i}$
,
$(\unicode[STIX]{x2202}^{2}n^{2}/\unicode[STIX]{x2202}t^{2})A_{i}$
,
![]() $(\unicode[STIX]{x2202}n^{2}/\unicode[STIX]{x2202}t)(\unicode[STIX]{x2202}A_{i}/\unicode[STIX]{x2202}t)$
and
$(\unicode[STIX]{x2202}n^{2}/\unicode[STIX]{x2202}t)(\unicode[STIX]{x2202}A_{i}/\unicode[STIX]{x2202}t)$
and
![]() $(\unicode[STIX]{x2202}n^{2}/\unicode[STIX]{x2202}t)\unicode[STIX]{x1D714}_{i}A_{i}$
are negligible.
$(\unicode[STIX]{x2202}n^{2}/\unicode[STIX]{x2202}t)\unicode[STIX]{x1D714}_{i}A_{i}$
are negligible.
![]() $2iw_{1}(\unicode[STIX]{x2202}A_{1}/\unicode[STIX]{x2202}t)$
and
$2iw_{1}(\unicode[STIX]{x2202}A_{1}/\unicode[STIX]{x2202}t)$
and
![]() $2iw_{2}(\unicode[STIX]{x2202}A_{2}/\unicode[STIX]{x2202}t)$
are also negligible since the light ray traversing time is on the order of 10 ns. Therefore, only the terms
$2iw_{2}(\unicode[STIX]{x2202}A_{2}/\unicode[STIX]{x2202}t)$
are also negligible since the light ray traversing time is on the order of 10 ns. Therefore, only the terms
![]() $n^{2}w_{1}^{2}A_{1}$
and
$n^{2}w_{1}^{2}A_{1}$
and
![]() $n^{2}w_{2}^{2}A_{2}$
are kept in Equation (6). Similar approximations are also used in Equation (7) where only the second derivative in time term generating
$n^{2}w_{2}^{2}A_{2}$
are kept in Equation (6). Similar approximations are also used in Equation (7) where only the second derivative in time term generating
![]() $\unicode[STIX]{x1D714}^{2}$
is retained. The terms that contain
$\unicode[STIX]{x1D714}^{2}$
is retained. The terms that contain
![]() $\unicode[STIX]{x2202}(\unicode[STIX]{x1D70E}_{s}^{e}N_{2}-\unicode[STIX]{x1D70E}_{s}^{a}N_{1})/\unicode[STIX]{x2202}t$
and
$\unicode[STIX]{x2202}(\unicode[STIX]{x1D70E}_{s}^{e}N_{2}-\unicode[STIX]{x1D70E}_{s}^{a}N_{1})/\unicode[STIX]{x2202}t$
and
![]() $\unicode[STIX]{x2202}^{2}(\unicode[STIX]{x1D70E}_{s}^{e}N_{2}-\unicode[STIX]{x1D70E}_{s}^{a}N_{1})/\unicode[STIX]{x2202}t^{2}$
are neglected as the laser gain response time is much greater than the optical period. We now substitute Equation (4) to Equation (7) and Equation (3) and we get
$\unicode[STIX]{x2202}^{2}(\unicode[STIX]{x1D70E}_{s}^{e}N_{2}-\unicode[STIX]{x1D70E}_{s}^{a}N_{1})/\unicode[STIX]{x2202}t^{2}$
are neglected as the laser gain response time is much greater than the optical period. We now substitute Equation (4) to Equation (7) and Equation (3) and we get
 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{1}{2}\left[A_{1}\unicode[STIX]{x1D6FB}_{t}^{2}\unicode[STIX]{x1D711}_{1}+(i\unicode[STIX]{x1D6FD}_{1}-\unicode[STIX]{x1D6FC}_{1})^{2}A_{1}\unicode[STIX]{x1D711}_{1}+\frac{n^{2}w_{1}^{2}}{c^{2}}A_{1}\unicode[STIX]{x1D711}_{1}\right.\nonumber\\ \displaystyle & & \displaystyle \qquad +\left.2\left(i\unicode[STIX]{x1D6FD}_{1}-\unicode[STIX]{x1D6FC}_{1}\right)_{1}\left(\frac{\unicode[STIX]{x2202}A_{1}}{\unicode[STIX]{x2202}z}\unicode[STIX]{x1D711}_{1}+\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{1}}{\unicode[STIX]{x2202}z}A_{1}\right)\right]e^{i(\unicode[STIX]{x1D6FD}_{1}z-w_{1}t)-\unicode[STIX]{x1D6FC}_{1}z}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{1}{2}\left[A_{2}\unicode[STIX]{x1D6FB}_{t}^{2}\unicode[STIX]{x1D711}_{2}+\left(i\unicode[STIX]{x1D6FD}_{2}-\unicode[STIX]{x1D6FC}_{2}\right)^{2}A_{2}\unicode[STIX]{x1D711}_{2}+\frac{n^{2}w_{2}^{2}}{c^{2}}A_{2}\unicode[STIX]{x1D711}_{2}\right.\nonumber\\ \displaystyle & & \displaystyle \qquad +\left.2(i\unicode[STIX]{x1D6FD}_{2}-\unicode[STIX]{x1D6FC}_{2})\left(\frac{\unicode[STIX]{x2202}A_{2}}{\unicode[STIX]{x2202}z}\unicode[STIX]{x1D711}_{2}+\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{2}}{\unicode[STIX]{x2202}z}A_{2}\right)\right]e^{i(\unicode[STIX]{x1D6FD}_{2}z-w_{2}t)-\unicode[STIX]{x1D6FC}_{2}z}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{2in_{0}}{c}\left(\frac{\unicode[STIX]{x1D70E}_{s}^{e}N_{2}-\unicode[STIX]{x1D70E}_{s}^{a}N_{1}}{2}\right)\times \left[\frac{1}{2}w_{1}A_{1}\unicode[STIX]{x1D711}_{1}e^{i(\unicode[STIX]{x1D6FD}_{1}z-w_{1}t)-\unicode[STIX]{x1D6FC}_{1}z}\right.\nonumber\\ \displaystyle & & \displaystyle \qquad +\left.\frac{1}{2}w_{2}A_{2}\unicode[STIX]{x1D711}_{2}e^{i(\unicode[STIX]{x1D6FD}_{2}z-w_{2}t)-\unicode[STIX]{x1D6FC}_{2}z}\right].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{1}{2}\left[A_{1}\unicode[STIX]{x1D6FB}_{t}^{2}\unicode[STIX]{x1D711}_{1}+(i\unicode[STIX]{x1D6FD}_{1}-\unicode[STIX]{x1D6FC}_{1})^{2}A_{1}\unicode[STIX]{x1D711}_{1}+\frac{n^{2}w_{1}^{2}}{c^{2}}A_{1}\unicode[STIX]{x1D711}_{1}\right.\nonumber\\ \displaystyle & & \displaystyle \qquad +\left.2\left(i\unicode[STIX]{x1D6FD}_{1}-\unicode[STIX]{x1D6FC}_{1}\right)_{1}\left(\frac{\unicode[STIX]{x2202}A_{1}}{\unicode[STIX]{x2202}z}\unicode[STIX]{x1D711}_{1}+\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{1}}{\unicode[STIX]{x2202}z}A_{1}\right)\right]e^{i(\unicode[STIX]{x1D6FD}_{1}z-w_{1}t)-\unicode[STIX]{x1D6FC}_{1}z}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{1}{2}\left[A_{2}\unicode[STIX]{x1D6FB}_{t}^{2}\unicode[STIX]{x1D711}_{2}+\left(i\unicode[STIX]{x1D6FD}_{2}-\unicode[STIX]{x1D6FC}_{2}\right)^{2}A_{2}\unicode[STIX]{x1D711}_{2}+\frac{n^{2}w_{2}^{2}}{c^{2}}A_{2}\unicode[STIX]{x1D711}_{2}\right.\nonumber\\ \displaystyle & & \displaystyle \qquad +\left.2(i\unicode[STIX]{x1D6FD}_{2}-\unicode[STIX]{x1D6FC}_{2})\left(\frac{\unicode[STIX]{x2202}A_{2}}{\unicode[STIX]{x2202}z}\unicode[STIX]{x1D711}_{2}+\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{2}}{\unicode[STIX]{x2202}z}A_{2}\right)\right]e^{i(\unicode[STIX]{x1D6FD}_{2}z-w_{2}t)-\unicode[STIX]{x1D6FC}_{2}z}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{2in_{0}}{c}\left(\frac{\unicode[STIX]{x1D70E}_{s}^{e}N_{2}-\unicode[STIX]{x1D70E}_{s}^{a}N_{1}}{2}\right)\times \left[\frac{1}{2}w_{1}A_{1}\unicode[STIX]{x1D711}_{1}e^{i(\unicode[STIX]{x1D6FD}_{1}z-w_{1}t)-\unicode[STIX]{x1D6FC}_{1}z}\right.\nonumber\\ \displaystyle & & \displaystyle \qquad +\left.\frac{1}{2}w_{2}A_{2}\unicode[STIX]{x1D711}_{2}e^{i(\unicode[STIX]{x1D6FD}_{2}z-w_{2}t)-\unicode[STIX]{x1D6FC}_{2}z}\right].\end{eqnarray}$$
In order to further simplify the above equation, we need to simplify the thermal dependent refractive index as
where
![]() $n_{0}$
is the refractive index under zero heat load and
$n_{0}$
is the refractive index under zero heat load and
![]() $\unicode[STIX]{x1D702}$
is the thermo-optic coefficient. The temperature distribution could be given by the appropriate Green function as[Reference Hansen, Alkeskjold, Broeng and Lægsgaard14]
$\unicode[STIX]{x1D702}$
is the thermo-optic coefficient. The temperature distribution could be given by the appropriate Green function as[Reference Hansen, Alkeskjold, Broeng and Lægsgaard14]
where
![]() $\unicode[STIX]{x1D705}$
stands for the thermal conductivity and
$\unicode[STIX]{x1D705}$
stands for the thermal conductivity and
![]() $Q$
is the heat load in the fiber core induced by the quantum defect, which is given by
$Q$
is the heat load in the fiber core induced by the quantum defect, which is given by
where
![]() $g$
is the gain coefficient.
$g$
is the gain coefficient.
![]() $\unicode[STIX]{x1D706}_{s}$
and
$\unicode[STIX]{x1D706}_{s}$
and
![]() $\unicode[STIX]{x1D706}_{p}$
are the wavelengths of the signal light and pump light, respectively. Here we only consider the heat load induced by the quantum defect and ignore other effects such as photodarkening and background loss. The signal intensity is as follows:
$\unicode[STIX]{x1D706}_{p}$
are the wavelengths of the signal light and pump light, respectively. Here we only consider the heat load induced by the quantum defect and ignore other effects such as photodarkening and background loss. The signal intensity is as follows:
 $$\begin{eqnarray}\displaystyle I_{s} & = & \displaystyle {\textstyle \frac{1}{2}}n_{0}\unicode[STIX]{x1D700}_{0}cE_{s}E_{s}^{\ast }=(I_{1}+I_{2})+\unicode[STIX]{x1D6FF}I\nonumber\\ \displaystyle & = & \displaystyle {\textstyle \frac{1}{2}}n_{0}\unicode[STIX]{x1D700}_{0}c(A_{1}A_{1}^{\ast }\unicode[STIX]{x1D711}_{1}\unicode[STIX]{x1D711}_{1}^{\ast }e^{-2\unicode[STIX]{x1D6FC}_{1}z}+A_{2}A_{2}^{\ast }\unicode[STIX]{x1D711}_{2}\unicode[STIX]{x1D711}_{2}^{\ast }e^{-2\unicode[STIX]{x1D6FC}_{2}z})\nonumber\\ \displaystyle & & \displaystyle +\,{\textstyle \frac{1}{2}}n_{0}\unicode[STIX]{x1D700}_{0}c[A_{1}A_{2}^{\ast }\unicode[STIX]{x1D711}_{1}\unicode[STIX]{x1D711}_{2}^{\ast }e^{i(qz-\unicode[STIX]{x1D6FA}t)-(\unicode[STIX]{x1D6FC}_{1}+\unicode[STIX]{x1D6FC}_{2})z}\nonumber\\ \displaystyle & & \displaystyle +\,A_{1}^{\ast }A_{2}\unicode[STIX]{x1D711}_{1}^{\ast }\unicode[STIX]{x1D711}_{2}e^{-i(qz-\unicode[STIX]{x1D6FA}t)-\left(\unicode[STIX]{x1D6FC}_{1}+\unicode[STIX]{x1D6FC}_{2}\right)z} ],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle I_{s} & = & \displaystyle {\textstyle \frac{1}{2}}n_{0}\unicode[STIX]{x1D700}_{0}cE_{s}E_{s}^{\ast }=(I_{1}+I_{2})+\unicode[STIX]{x1D6FF}I\nonumber\\ \displaystyle & = & \displaystyle {\textstyle \frac{1}{2}}n_{0}\unicode[STIX]{x1D700}_{0}c(A_{1}A_{1}^{\ast }\unicode[STIX]{x1D711}_{1}\unicode[STIX]{x1D711}_{1}^{\ast }e^{-2\unicode[STIX]{x1D6FC}_{1}z}+A_{2}A_{2}^{\ast }\unicode[STIX]{x1D711}_{2}\unicode[STIX]{x1D711}_{2}^{\ast }e^{-2\unicode[STIX]{x1D6FC}_{2}z})\nonumber\\ \displaystyle & & \displaystyle +\,{\textstyle \frac{1}{2}}n_{0}\unicode[STIX]{x1D700}_{0}c[A_{1}A_{2}^{\ast }\unicode[STIX]{x1D711}_{1}\unicode[STIX]{x1D711}_{2}^{\ast }e^{i(qz-\unicode[STIX]{x1D6FA}t)-(\unicode[STIX]{x1D6FC}_{1}+\unicode[STIX]{x1D6FC}_{2})z}\nonumber\\ \displaystyle & & \displaystyle +\,A_{1}^{\ast }A_{2}\unicode[STIX]{x1D711}_{1}^{\ast }\unicode[STIX]{x1D711}_{2}e^{-i(qz-\unicode[STIX]{x1D6FA}t)-\left(\unicode[STIX]{x1D6FC}_{1}+\unicode[STIX]{x1D6FC}_{2}\right)z} ],\end{eqnarray}$$
where
![]() $I_{1}$
and
$I_{1}$
and
![]() $I_{2}$
are intensities of the FM and HOM, respectively,
$I_{2}$
are intensities of the FM and HOM, respectively,
![]() $\unicode[STIX]{x1D6FF}I$
represents the mode beating pattern,
$\unicode[STIX]{x1D6FF}I$
represents the mode beating pattern,
![]() $q=\unicode[STIX]{x1D6FD}_{1}-\unicode[STIX]{x1D6FD}_{2}$
and
$q=\unicode[STIX]{x1D6FD}_{1}-\unicode[STIX]{x1D6FD}_{2}$
and
![]() $\unicode[STIX]{x1D6FA}=w_{1}-w_{2}$
.
$\unicode[STIX]{x1D6FA}=w_{1}-w_{2}$
.
![]() $\unicode[STIX]{x1D700}_{0}$
and
$\unicode[STIX]{x1D700}_{0}$
and
![]() $n_{0}$
are the vacuum permittivity and the refractive index of the silica (1.45), respectively. We now substitute Equation (10) to Equation (12) and Equation (9) and obtain the expression for the refractive index:
$n_{0}$
are the vacuum permittivity and the refractive index of the silica (1.45), respectively. We now substitute Equation (10) to Equation (12) and Equation (9) and obtain the expression for the refractive index:
It is obvious that there are two kinds of refractive index changes defined as
 $$\begin{eqnarray}\begin{array}{@{}l@{}}\unicode[STIX]{x1D6FF}n_{1}=\unicode[STIX]{x1D702}\left({\displaystyle \frac{\unicode[STIX]{x1D706}_{s}}{\unicode[STIX]{x1D706}_{p}}}-1\right)\displaystyle \int _{\unicode[STIX]{x1D70F}=0}^{t}\displaystyle \int \frac{1}{\unicode[STIX]{x1D705}}Gg(I_{1}+I_{2})\,\text{d}\overset{\rightharpoonup }{r}^{\prime }\text{d}\unicode[STIX]{x1D70F}\\ \unicode[STIX]{x1D6FF}n_{2}=\unicode[STIX]{x1D702}\left({\displaystyle \frac{\unicode[STIX]{x1D706}_{s}}{\unicode[STIX]{x1D706}_{p}}}-1\right)\displaystyle \int _{\unicode[STIX]{x1D70F}=0}^{t}\displaystyle \int \frac{1}{\unicode[STIX]{x1D705}}Gg\unicode[STIX]{x1D6FF}I\,\text{d}\overset{\rightharpoonup }{r}^{\prime }\text{d}\unicode[STIX]{x1D70F}.\quad \end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}l@{}}\unicode[STIX]{x1D6FF}n_{1}=\unicode[STIX]{x1D702}\left({\displaystyle \frac{\unicode[STIX]{x1D706}_{s}}{\unicode[STIX]{x1D706}_{p}}}-1\right)\displaystyle \int _{\unicode[STIX]{x1D70F}=0}^{t}\displaystyle \int \frac{1}{\unicode[STIX]{x1D705}}Gg(I_{1}+I_{2})\,\text{d}\overset{\rightharpoonup }{r}^{\prime }\text{d}\unicode[STIX]{x1D70F}\\ \unicode[STIX]{x1D6FF}n_{2}=\unicode[STIX]{x1D702}\left({\displaystyle \frac{\unicode[STIX]{x1D706}_{s}}{\unicode[STIX]{x1D706}_{p}}}-1\right)\displaystyle \int _{\unicode[STIX]{x1D70F}=0}^{t}\displaystyle \int \frac{1}{\unicode[STIX]{x1D705}}Gg\unicode[STIX]{x1D6FF}I\,\text{d}\overset{\rightharpoonup }{r}^{\prime }\text{d}\unicode[STIX]{x1D70F}.\quad \end{array}\end{eqnarray}$$
The first kind of refractive index change
![]() $\unicode[STIX]{x1D6FF}n_{1}$
is a refractive index change due to the heat load induced by the signal power amplification. The second kind
$\unicode[STIX]{x1D6FF}n_{1}$
is a refractive index change due to the heat load induced by the signal power amplification. The second kind
![]() $\unicode[STIX]{x1D6FF}n_{2}$
is a refractive index change due to the mode beating, namely, the long period grating (LPG). Apparently,
$\unicode[STIX]{x1D6FF}n_{2}$
is a refractive index change due to the mode beating, namely, the long period grating (LPG). Apparently,
![]() $\unicode[STIX]{x1D6FF}n_{1}$
is a time-independent term that does not contribute to the mode coupling. However,
$\unicode[STIX]{x1D6FF}n_{1}$
is a time-independent term that does not contribute to the mode coupling. However,
![]() $\unicode[STIX]{x1D6FF}n_{1}$
will contribute to the local refractive index change, which leads to the local mode properties variation. This will allow us to introduce the local mode theory into the coupled-mode equation. We define the local modes as follows:
$\unicode[STIX]{x1D6FF}n_{1}$
will contribute to the local refractive index change, which leads to the local mode properties variation. This will allow us to introduce the local mode theory into the coupled-mode equation. We define the local modes as follows:
 $$\begin{eqnarray}\begin{array}{@{}l@{}}\unicode[STIX]{x1D6FB}_{t}^{2}\unicode[STIX]{x1D711}_{1}-(i\unicode[STIX]{x1D6FD}_{1}-\unicode[STIX]{x1D6FC}_{1})^{2}\unicode[STIX]{x1D711}_{1}+{\displaystyle \frac{(n_{0}+\unicode[STIX]{x1D6FF}n_{1})^{2}w_{1}^{2}}{c^{2}}}\unicode[STIX]{x1D711}_{1}=0\\ \unicode[STIX]{x1D6FB}_{t}^{2}\unicode[STIX]{x1D711}_{2}-(i\unicode[STIX]{x1D6FD}_{2}-\unicode[STIX]{x1D6FC}_{2})^{2}\unicode[STIX]{x1D711}_{2}+{\displaystyle \frac{(n_{0}+\unicode[STIX]{x1D6FF}n_{1})^{2}w_{2}^{2}}{c^{2}}}\unicode[STIX]{x1D711}_{2}=0,\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}l@{}}\unicode[STIX]{x1D6FB}_{t}^{2}\unicode[STIX]{x1D711}_{1}-(i\unicode[STIX]{x1D6FD}_{1}-\unicode[STIX]{x1D6FC}_{1})^{2}\unicode[STIX]{x1D711}_{1}+{\displaystyle \frac{(n_{0}+\unicode[STIX]{x1D6FF}n_{1})^{2}w_{1}^{2}}{c^{2}}}\unicode[STIX]{x1D711}_{1}=0\\ \unicode[STIX]{x1D6FB}_{t}^{2}\unicode[STIX]{x1D711}_{2}-(i\unicode[STIX]{x1D6FD}_{2}-\unicode[STIX]{x1D6FC}_{2})^{2}\unicode[STIX]{x1D711}_{2}+{\displaystyle \frac{(n_{0}+\unicode[STIX]{x1D6FF}n_{1})^{2}w_{2}^{2}}{c^{2}}}\unicode[STIX]{x1D711}_{2}=0,\end{array}\end{eqnarray}$$
where the mode properties depend on the local refractive index due to local heat load. In this paper, we assume that the thermal load produced by the signal amplification is equivalent to the thermal load of the absorption of the pump light. This approximation will greatly reduce the calculation time since pump power is uniformly distributed inside the core and the temperature distribution could be obtained analytically[Reference Kong, Leng, Zhou and Jiang20]. Thus
![]() $\unicode[STIX]{x1D6FF}n_{1}$
is as follows:
$\unicode[STIX]{x1D6FF}n_{1}$
is as follows:
 $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6FF}n_{1}(q,r,\unicode[STIX]{x1D703})\nonumber\\ \displaystyle & & \displaystyle \quad =\left\{\begin{array}{@{}l@{}}\hspace{-5.0pt}\left\{n_{\text{core}}+\unicode[STIX]{x1D702}\left[\!{\displaystyle \frac{q(a^{2}-r^{2})}{4k_{si}}}+{\displaystyle \frac{qa^{2}}{2k_{si}}}\ln \left(\!{\displaystyle \frac{b}{a}}\!\right)\right.\right.\quad \\ \hspace{-9.0pt}\quad \left.\left.+\,{\displaystyle \frac{qa^{2}}{2k_{ac}}}\ln \left({\displaystyle \frac{c}{a}}\right)\!\right]\right\}\sqrt{1+{\displaystyle \frac{2r}{\unicode[STIX]{x1D70C}R}}\cos \unicode[STIX]{x1D703}},\quad 0\leqslant r\leqslant a,\quad \\ \hspace{-5.0pt}\left\{n_{\text{clad}}+\unicode[STIX]{x1D702}\left[{\displaystyle \frac{qa^{2}}{2k_{si}}}\ln \left({\displaystyle \frac{b}{r}}\right)+{\displaystyle \frac{qa^{2}}{2k_{ac}}}\ln \left({\displaystyle \frac{c}{b}}\right)\right]\right\}\quad \\ \hspace{-8.0pt}\quad \times \sqrt{1+{\displaystyle \frac{2r}{\unicode[STIX]{x1D70C}R}}\cos \unicode[STIX]{x1D703}},\quad a\leqslant r\leqslant b,\quad \end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6FF}n_{1}(q,r,\unicode[STIX]{x1D703})\nonumber\\ \displaystyle & & \displaystyle \quad =\left\{\begin{array}{@{}l@{}}\hspace{-5.0pt}\left\{n_{\text{core}}+\unicode[STIX]{x1D702}\left[\!{\displaystyle \frac{q(a^{2}-r^{2})}{4k_{si}}}+{\displaystyle \frac{qa^{2}}{2k_{si}}}\ln \left(\!{\displaystyle \frac{b}{a}}\!\right)\right.\right.\quad \\ \hspace{-9.0pt}\quad \left.\left.+\,{\displaystyle \frac{qa^{2}}{2k_{ac}}}\ln \left({\displaystyle \frac{c}{a}}\right)\!\right]\right\}\sqrt{1+{\displaystyle \frac{2r}{\unicode[STIX]{x1D70C}R}}\cos \unicode[STIX]{x1D703}},\quad 0\leqslant r\leqslant a,\quad \\ \hspace{-5.0pt}\left\{n_{\text{clad}}+\unicode[STIX]{x1D702}\left[{\displaystyle \frac{qa^{2}}{2k_{si}}}\ln \left({\displaystyle \frac{b}{r}}\right)+{\displaystyle \frac{qa^{2}}{2k_{ac}}}\ln \left({\displaystyle \frac{c}{b}}\right)\right]\right\}\quad \\ \hspace{-8.0pt}\quad \times \sqrt{1+{\displaystyle \frac{2r}{\unicode[STIX]{x1D70C}R}}\cos \unicode[STIX]{x1D703}},\quad a\leqslant r\leqslant b,\quad \end{array}\right.\end{eqnarray}$$
where
![]() $n_{\text{core}}$
and
$n_{\text{core}}$
and
![]() $n_{\text{clad}}$
are the original refractive indices of the core and cladding, respectively.
$n_{\text{clad}}$
are the original refractive indices of the core and cladding, respectively.
![]() $a$
,
$a$
,
![]() $b$
and
$b$
and
![]() $c$
are the radii of doped core, cladding and coating, respectively.
$c$
are the radii of doped core, cladding and coating, respectively.
![]() $k_{si}$
and
$k_{si}$
and
![]() $k_{ac}$
represent the thermal conductivity for the silica and coating material, respectively.
$k_{ac}$
represent the thermal conductivity for the silica and coating material, respectively.
![]() $R$
is the bending radius,
$R$
is the bending radius,
![]() $\unicode[STIX]{x1D703}$
is the azimuthal angle and
$\unicode[STIX]{x1D703}$
is the azimuthal angle and
![]() $\unicode[STIX]{x1D70C}$
is account of the stress factor. The heat load density
$\unicode[STIX]{x1D70C}$
is account of the stress factor. The heat load density
![]() $q$
is as follows:
$q$
is as follows:
 $$\begin{eqnarray}\displaystyle q(z) & = & \displaystyle \frac{Q_{p}(z)}{\unicode[STIX]{x1D70B}a^{2}}=\frac{1}{\unicode[STIX]{x1D70B}a^{2}}\times \left(\frac{\unicode[STIX]{x1D706}_{s}}{\unicode[STIX]{x1D706}_{p}}-1\right)\nonumber\\ \displaystyle & & \displaystyle \times \,\left[\frac{\text{d}\!P_{p}^{-}(z)}{\text{d}z}-\frac{\text{d}\!P_{p}^{+}(z)}{\text{d}z}\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle q(z) & = & \displaystyle \frac{Q_{p}(z)}{\unicode[STIX]{x1D70B}a^{2}}=\frac{1}{\unicode[STIX]{x1D70B}a^{2}}\times \left(\frac{\unicode[STIX]{x1D706}_{s}}{\unicode[STIX]{x1D706}_{p}}-1\right)\nonumber\\ \displaystyle & & \displaystyle \times \,\left[\frac{\text{d}\!P_{p}^{-}(z)}{\text{d}z}-\frac{\text{d}\!P_{p}^{+}(z)}{\text{d}z}\right],\end{eqnarray}$$
where
![]() $Q_{p}(z)$
stands for the heat load along the active fiber due to pump absorption,
$Q_{p}(z)$
stands for the heat load along the active fiber due to pump absorption,
![]() $P_{p}^{+}(z)$
and
$P_{p}^{+}(z)$
and
![]() $P_{p}^{-}(z)$
are the co-propagating and counter-propagating pump powers, respectively. Then, the local mode properties such as mode field, mode effective refractive index and mode loss could be obtained according to Equation (16) via conventional finite element method (FEM) mode solver[Reference Kong, Leng, Zhou and Jiang20, Reference Dong24]. It should be noted that in the model given by Hansen et al.,
$P_{p}^{-}(z)$
are the co-propagating and counter-propagating pump powers, respectively. Then, the local mode properties such as mode field, mode effective refractive index and mode loss could be obtained according to Equation (16) via conventional finite element method (FEM) mode solver[Reference Kong, Leng, Zhou and Jiang20, Reference Dong24]. It should be noted that in the model given by Hansen et al.,
![]() $n_{1}$
is treated as the phase modulation since they assume that the mode properties does not change due to the thermal effect[Reference Hansen, Alkeskjold, Broeng and Lægsgaard14]. In fact, the mode properties variation and the phase modulation are physically equivalent since the mode effective refractive index change will lead to the change of mode propagation phase.
$n_{1}$
is treated as the phase modulation since they assume that the mode properties does not change due to the thermal effect[Reference Hansen, Alkeskjold, Broeng and Lægsgaard14]. In fact, the mode properties variation and the phase modulation are physically equivalent since the mode effective refractive index change will lead to the change of mode propagation phase.
Substituting Equation (14) into Equation (13), the thermally dependent refractive index could be written as
where the higher-order index changes are ignored. Then, substituting Equation (15) and Equation (18) into Equation (8), we get the simplified wave equation:
 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{1}{2}\left[\frac{2n_{0}n_{2}w_{1}^{2}}{c^{2}}A_{1}\unicode[STIX]{x1D711}_{1}+2(i\unicode[STIX]{x1D6FD}_{1}-\unicode[STIX]{x1D6FC}_{1})\right.\nonumber\\ \displaystyle & & \displaystyle \qquad \times \left.\left(\frac{\unicode[STIX]{x2202}A_{1}}{\unicode[STIX]{x2202}z}\unicode[STIX]{x1D711}_{1}+\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{1}}{\unicode[STIX]{x2202}z}A_{1}\right)\vphantom{\frac{2n_{0}n_{2}w_{1}^{2}}{c^{2}}}\!\right]e^{i(\unicode[STIX]{x1D6FD}_{1}z-w_{1}t)-\unicode[STIX]{x1D6FC}_{1}z}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{1}{2}\left[\frac{2n_{0}n_{2}w_{2}^{2}}{c^{2}}A_{2}\unicode[STIX]{x1D711}_{2}+2\left(i\unicode[STIX]{x1D6FD}_{2}-\unicode[STIX]{x1D6FC}_{2}\right)\right.\nonumber\\ \displaystyle & & \displaystyle \qquad \times \left.\left(\frac{\unicode[STIX]{x2202}A_{2}}{\unicode[STIX]{x2202}z}\unicode[STIX]{x1D711}_{2}+\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{2}}{\unicode[STIX]{x2202}z}A_{2}\right)\vphantom{\frac{2n_{0}n_{2}w_{1}^{2}}{c^{2}}}\!\right]e^{i(\unicode[STIX]{x1D6FD}_{2}z-w_{2}t)-\unicode[STIX]{x1D6FC}_{2}z}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{2in_{0}}{c}\left(\frac{\unicode[STIX]{x1D70E}_{s}^{e}N_{2}-\unicode[STIX]{x1D70E}_{s}^{a}N_{1}}{2}\right)\times \left[\frac{1}{2}w_{1}A_{1}\unicode[STIX]{x1D711}_{1}e^{i(\unicode[STIX]{x1D6FD}_{1}z-w_{1}t)-\unicode[STIX]{x1D6FC}_{1}z}\right.\nonumber\\ \displaystyle & & \displaystyle \qquad +\left.\frac{1}{2}w_{2}A_{2}\unicode[STIX]{x1D711}_{2}e^{i(\unicode[STIX]{x1D6FD}_{2}z-w_{2}t)-\unicode[STIX]{x1D6FC}_{2}z}\right].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{1}{2}\left[\frac{2n_{0}n_{2}w_{1}^{2}}{c^{2}}A_{1}\unicode[STIX]{x1D711}_{1}+2(i\unicode[STIX]{x1D6FD}_{1}-\unicode[STIX]{x1D6FC}_{1})\right.\nonumber\\ \displaystyle & & \displaystyle \qquad \times \left.\left(\frac{\unicode[STIX]{x2202}A_{1}}{\unicode[STIX]{x2202}z}\unicode[STIX]{x1D711}_{1}+\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{1}}{\unicode[STIX]{x2202}z}A_{1}\right)\vphantom{\frac{2n_{0}n_{2}w_{1}^{2}}{c^{2}}}\!\right]e^{i(\unicode[STIX]{x1D6FD}_{1}z-w_{1}t)-\unicode[STIX]{x1D6FC}_{1}z}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{1}{2}\left[\frac{2n_{0}n_{2}w_{2}^{2}}{c^{2}}A_{2}\unicode[STIX]{x1D711}_{2}+2\left(i\unicode[STIX]{x1D6FD}_{2}-\unicode[STIX]{x1D6FC}_{2}\right)\right.\nonumber\\ \displaystyle & & \displaystyle \qquad \times \left.\left(\frac{\unicode[STIX]{x2202}A_{2}}{\unicode[STIX]{x2202}z}\unicode[STIX]{x1D711}_{2}+\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{2}}{\unicode[STIX]{x2202}z}A_{2}\right)\vphantom{\frac{2n_{0}n_{2}w_{1}^{2}}{c^{2}}}\!\right]e^{i(\unicode[STIX]{x1D6FD}_{2}z-w_{2}t)-\unicode[STIX]{x1D6FC}_{2}z}\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{2in_{0}}{c}\left(\frac{\unicode[STIX]{x1D70E}_{s}^{e}N_{2}-\unicode[STIX]{x1D70E}_{s}^{a}N_{1}}{2}\right)\times \left[\frac{1}{2}w_{1}A_{1}\unicode[STIX]{x1D711}_{1}e^{i(\unicode[STIX]{x1D6FD}_{1}z-w_{1}t)-\unicode[STIX]{x1D6FC}_{1}z}\right.\nonumber\\ \displaystyle & & \displaystyle \qquad +\left.\frac{1}{2}w_{2}A_{2}\unicode[STIX]{x1D711}_{2}e^{i(\unicode[STIX]{x1D6FD}_{2}z-w_{2}t)-\unicode[STIX]{x1D6FC}_{2}z}\right].\end{eqnarray}$$
The normalized mode field satisfies the orthonormality property, which is defined as
Practically, the propagation constant is at the order of
![]() $10^{6}$
, which is much larger than the mode loss of FM and HOM, namely,
$10^{6}$
, which is much larger than the mode loss of FM and HOM, namely,
![]() $\unicode[STIX]{x1D6FD}_{1}\gg \unicode[STIX]{x1D6FC}_{1}$
and
$\unicode[STIX]{x1D6FD}_{1}\gg \unicode[STIX]{x1D6FC}_{1}$
and
![]() $\unicode[STIX]{x1D6FD}_{2}\gg \unicode[STIX]{x1D6FC}_{2}$
. We also assume that
$\unicode[STIX]{x1D6FD}_{2}\gg \unicode[STIX]{x1D6FC}_{2}$
. We also assume that
![]() $n_{0}w_{1}/c\unicode[STIX]{x1D6FD}_{1}\approx 1$
and
$n_{0}w_{1}/c\unicode[STIX]{x1D6FD}_{1}\approx 1$
and
![]() $n_{0}w_{2}/c\unicode[STIX]{x1D6FD}_{2}\approx 1$
. Based on the orthonormality property and these two approximations, we could simplify Equation (19) into the coupled-mode equations as follows:
$n_{0}w_{2}/c\unicode[STIX]{x1D6FD}_{2}\approx 1$
. Based on the orthonormality property and these two approximations, we could simplify Equation (19) into the coupled-mode equations as follows:
 $$\begin{eqnarray}\displaystyle {\displaystyle \frac{\unicode[STIX]{x2202}A_{1}}{\unicode[STIX]{x2202}z}} & = & \displaystyle {\displaystyle \frac{\unicode[STIX]{x1D6E4}_{1}}{2}}A_{1}g+{\displaystyle \frac{i\unicode[STIX]{x1D6FD}_{1}}{n_{0}}}A_{2}e^{-i(qz-\unicode[STIX]{x1D6FA}t)+\unicode[STIX]{x1D6EC}z}\displaystyle \int \unicode[STIX]{x1D6FF}n_{2}\unicode[STIX]{x1D711}_{2}\unicode[STIX]{x1D711}_{1}^{\ast }\,\text{d}A\nonumber\\ \displaystyle & & \displaystyle -{\displaystyle \frac{\unicode[STIX]{x1D6FD}_{2}}{\unicode[STIX]{x1D6FD}_{1}}}A_{2}e^{-i(qz-\unicode[STIX]{x1D6FA}t)+\unicode[STIX]{x1D6EC}z}\displaystyle \int \unicode[STIX]{x1D711}_{1}^{\ast }\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{2}}{\unicode[STIX]{x2202}z}\,\text{d}A,\nonumber\\ \displaystyle {\displaystyle \frac{\unicode[STIX]{x2202}A_{2}}{\unicode[STIX]{x2202}z}} & = & \displaystyle {\displaystyle \frac{\unicode[STIX]{x1D6E4}_{2}}{2}}A_{2}g+{\displaystyle \frac{i\unicode[STIX]{x1D6FD}_{2}}{n_{0}}}A_{1}e^{i(qz-\unicode[STIX]{x1D6FA}t)-\unicode[STIX]{x1D6EC}z}\displaystyle \int \unicode[STIX]{x1D6FF}n_{2}\unicode[STIX]{x1D711}_{1}\unicode[STIX]{x1D711}_{2}^{\ast }\,\text{d}A\nonumber\\ \displaystyle & & \displaystyle -{\displaystyle \frac{\unicode[STIX]{x1D6FD}_{1}}{\unicode[STIX]{x1D6FD}_{2}}}A_{1}e^{i(qz-\unicode[STIX]{x1D6FA}t)-\unicode[STIX]{x1D6EC}z}\displaystyle \int {\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{1}}{\unicode[STIX]{x2202}z}}\unicode[STIX]{x1D711}_{2}^{\ast }\,\text{d}A,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\displaystyle \frac{\unicode[STIX]{x2202}A_{1}}{\unicode[STIX]{x2202}z}} & = & \displaystyle {\displaystyle \frac{\unicode[STIX]{x1D6E4}_{1}}{2}}A_{1}g+{\displaystyle \frac{i\unicode[STIX]{x1D6FD}_{1}}{n_{0}}}A_{2}e^{-i(qz-\unicode[STIX]{x1D6FA}t)+\unicode[STIX]{x1D6EC}z}\displaystyle \int \unicode[STIX]{x1D6FF}n_{2}\unicode[STIX]{x1D711}_{2}\unicode[STIX]{x1D711}_{1}^{\ast }\,\text{d}A\nonumber\\ \displaystyle & & \displaystyle -{\displaystyle \frac{\unicode[STIX]{x1D6FD}_{2}}{\unicode[STIX]{x1D6FD}_{1}}}A_{2}e^{-i(qz-\unicode[STIX]{x1D6FA}t)+\unicode[STIX]{x1D6EC}z}\displaystyle \int \unicode[STIX]{x1D711}_{1}^{\ast }\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{2}}{\unicode[STIX]{x2202}z}\,\text{d}A,\nonumber\\ \displaystyle {\displaystyle \frac{\unicode[STIX]{x2202}A_{2}}{\unicode[STIX]{x2202}z}} & = & \displaystyle {\displaystyle \frac{\unicode[STIX]{x1D6E4}_{2}}{2}}A_{2}g+{\displaystyle \frac{i\unicode[STIX]{x1D6FD}_{2}}{n_{0}}}A_{1}e^{i(qz-\unicode[STIX]{x1D6FA}t)-\unicode[STIX]{x1D6EC}z}\displaystyle \int \unicode[STIX]{x1D6FF}n_{2}\unicode[STIX]{x1D711}_{1}\unicode[STIX]{x1D711}_{2}^{\ast }\,\text{d}A\nonumber\\ \displaystyle & & \displaystyle -{\displaystyle \frac{\unicode[STIX]{x1D6FD}_{1}}{\unicode[STIX]{x1D6FD}_{2}}}A_{1}e^{i(qz-\unicode[STIX]{x1D6FA}t)-\unicode[STIX]{x1D6EC}z}\displaystyle \int {\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}_{1}}{\unicode[STIX]{x2202}z}}\unicode[STIX]{x1D711}_{2}^{\ast }\,\text{d}A,\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D6E4}_{1}$
and
$\unicode[STIX]{x1D6E4}_{1}$
and
![]() $\unicode[STIX]{x1D6E4}_{2}$
are the filling factors of the local FM and HOM, respectively.
$\unicode[STIX]{x1D6E4}_{2}$
are the filling factors of the local FM and HOM, respectively.
![]() $\unicode[STIX]{x1D6EC}$
equals the mode loss difference between the FM and the HOM, namely
$\unicode[STIX]{x1D6EC}$
equals the mode loss difference between the FM and the HOM, namely
![]() $\unicode[STIX]{x1D6FC}_{1}-\unicode[STIX]{x1D6FC}_{2}$
.
$\unicode[STIX]{x1D6FC}_{1}-\unicode[STIX]{x1D6FC}_{2}$
.
![]() $g$
is the gain coefficient defined as
$g$
is the gain coefficient defined as
In this paper, we ignore the third term on the RHS since we only focus on the mode coupling in the conventional
![]() $20/400$
fiber. This assumption will breakdown for the fiber with very large mode area (LMA)[Reference Hansen, Alkeskjold, Broeng and Lægsgaard25, Reference Hansen, Alkeskjold, Broeng and Lægsgaard26]. Substituting Equation (14) into Equation (21) and only considering the phase matched term, we obtain
$20/400$
fiber. This assumption will breakdown for the fiber with very large mode area (LMA)[Reference Hansen, Alkeskjold, Broeng and Lægsgaard25, Reference Hansen, Alkeskjold, Broeng and Lægsgaard26]. Substituting Equation (14) into Equation (21) and only considering the phase matched term, we obtain
 $$\begin{eqnarray}\displaystyle {\displaystyle \frac{\unicode[STIX]{x2202}A_{1}}{\unicode[STIX]{x2202}z}} & = & \displaystyle {\displaystyle \frac{\unicode[STIX]{x1D6E4}_{1}}{2}}A_{1}g+{\displaystyle \frac{1}{2}}n_{0}\unicode[STIX]{x1D700}_{0}cA_{2}A_{2}^{\ast }e^{-2\unicode[STIX]{x1D6FC}_{2}z}A_{1}g_{\text{sat}}\nonumber\\ \displaystyle & & \displaystyle \times \,\left\{{\displaystyle \frac{i\unicode[STIX]{x1D702}\unicode[STIX]{x1D6FD}_{1}}{n_{0}}}\left({\displaystyle \frac{\unicode[STIX]{x1D706}_{s}}{\unicode[STIX]{x1D706}_{p}}}-1\right)\right.\nonumber\\ \displaystyle & & \displaystyle \times \,\left\{\displaystyle \int \left[\displaystyle \int _{\unicode[STIX]{x1D70F}=0}^{t}\displaystyle \int {\displaystyle \frac{1}{\unicode[STIX]{x1D705}}}G\unicode[STIX]{x1D711}_{1}\unicode[STIX]{x1D711}_{2}^{\ast }e^{-i\unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D70F}-t)}\,\text{d}A^{\prime }\text{d}\unicode[STIX]{x1D70F}\right]\right.\nonumber\\ \displaystyle & & \displaystyle \times \left.\left.\unicode[STIX]{x1D711}_{2}\unicode[STIX]{x1D711}_{1}^{\ast }\,\text{d}A\vphantom{\left(\displaystyle \int _{\unicode[STIX]{x1D70F}=0}^{t}\displaystyle \int {\displaystyle \frac{1}{\unicode[STIX]{x1D705}}}G\unicode[STIX]{x1D711}_{1}\unicode[STIX]{x1D711}_{2}^{\ast }e^{-i\unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D70F}-t)}\,dA^{\prime }\text{d}\unicode[STIX]{x1D70F}\right)}\right\}\right\},\nonumber\\ \displaystyle {\displaystyle \frac{\unicode[STIX]{x2202}A_{2}}{\unicode[STIX]{x2202}z}} & = & \displaystyle {\displaystyle \frac{\unicode[STIX]{x1D6E4}_{2}}{2}}A_{2}g+{\displaystyle \frac{1}{2}}n_{0}\unicode[STIX]{x1D700}_{0}cA_{1}A_{1}^{\ast }e^{-2\unicode[STIX]{x1D6FC}_{1}z}A_{2}g_{\text{sat}}\nonumber\\ \displaystyle & & \displaystyle \times \,\left\{{\displaystyle \frac{i\unicode[STIX]{x1D702}\unicode[STIX]{x1D6FD}_{2}}{n_{0}}}\left({\displaystyle \frac{\unicode[STIX]{x1D706}_{s}}{\unicode[STIX]{x1D706}_{p}}}-1\right)\right.\nonumber\\ \displaystyle & & \displaystyle \times \,\left\{\displaystyle \int \left[\displaystyle \int _{\unicode[STIX]{x1D70F}=0}^{t}\displaystyle \int {\displaystyle \frac{1}{\unicode[STIX]{x1D705}}}G\unicode[STIX]{x1D711}_{1}^{\ast }\unicode[STIX]{x1D711}_{2}e^{i\unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D70F}-t)}\,\text{d}A^{\prime }\text{d}\unicode[STIX]{x1D70F}\right]\right.\nonumber\\ \displaystyle & & \displaystyle \times \left.\left.\unicode[STIX]{x1D711}_{1}\unicode[STIX]{x1D711}_{2}^{\ast }\,\text{d}A\vphantom{\left(\displaystyle \int _{\unicode[STIX]{x1D70F}=0}^{t}\displaystyle \int {\displaystyle \frac{1}{\unicode[STIX]{x1D705}}}G\unicode[STIX]{x1D711}_{1}\unicode[STIX]{x1D711}_{2}^{\ast }e^{-i\unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D70F}-t)}\,dA^{\prime }d\unicode[STIX]{x1D70F}\right)}\right\}\right\}\!,\quad\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\displaystyle \frac{\unicode[STIX]{x2202}A_{1}}{\unicode[STIX]{x2202}z}} & = & \displaystyle {\displaystyle \frac{\unicode[STIX]{x1D6E4}_{1}}{2}}A_{1}g+{\displaystyle \frac{1}{2}}n_{0}\unicode[STIX]{x1D700}_{0}cA_{2}A_{2}^{\ast }e^{-2\unicode[STIX]{x1D6FC}_{2}z}A_{1}g_{\text{sat}}\nonumber\\ \displaystyle & & \displaystyle \times \,\left\{{\displaystyle \frac{i\unicode[STIX]{x1D702}\unicode[STIX]{x1D6FD}_{1}}{n_{0}}}\left({\displaystyle \frac{\unicode[STIX]{x1D706}_{s}}{\unicode[STIX]{x1D706}_{p}}}-1\right)\right.\nonumber\\ \displaystyle & & \displaystyle \times \,\left\{\displaystyle \int \left[\displaystyle \int _{\unicode[STIX]{x1D70F}=0}^{t}\displaystyle \int {\displaystyle \frac{1}{\unicode[STIX]{x1D705}}}G\unicode[STIX]{x1D711}_{1}\unicode[STIX]{x1D711}_{2}^{\ast }e^{-i\unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D70F}-t)}\,\text{d}A^{\prime }\text{d}\unicode[STIX]{x1D70F}\right]\right.\nonumber\\ \displaystyle & & \displaystyle \times \left.\left.\unicode[STIX]{x1D711}_{2}\unicode[STIX]{x1D711}_{1}^{\ast }\,\text{d}A\vphantom{\left(\displaystyle \int _{\unicode[STIX]{x1D70F}=0}^{t}\displaystyle \int {\displaystyle \frac{1}{\unicode[STIX]{x1D705}}}G\unicode[STIX]{x1D711}_{1}\unicode[STIX]{x1D711}_{2}^{\ast }e^{-i\unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D70F}-t)}\,dA^{\prime }\text{d}\unicode[STIX]{x1D70F}\right)}\right\}\right\},\nonumber\\ \displaystyle {\displaystyle \frac{\unicode[STIX]{x2202}A_{2}}{\unicode[STIX]{x2202}z}} & = & \displaystyle {\displaystyle \frac{\unicode[STIX]{x1D6E4}_{2}}{2}}A_{2}g+{\displaystyle \frac{1}{2}}n_{0}\unicode[STIX]{x1D700}_{0}cA_{1}A_{1}^{\ast }e^{-2\unicode[STIX]{x1D6FC}_{1}z}A_{2}g_{\text{sat}}\nonumber\\ \displaystyle & & \displaystyle \times \,\left\{{\displaystyle \frac{i\unicode[STIX]{x1D702}\unicode[STIX]{x1D6FD}_{2}}{n_{0}}}\left({\displaystyle \frac{\unicode[STIX]{x1D706}_{s}}{\unicode[STIX]{x1D706}_{p}}}-1\right)\right.\nonumber\\ \displaystyle & & \displaystyle \times \,\left\{\displaystyle \int \left[\displaystyle \int _{\unicode[STIX]{x1D70F}=0}^{t}\displaystyle \int {\displaystyle \frac{1}{\unicode[STIX]{x1D705}}}G\unicode[STIX]{x1D711}_{1}^{\ast }\unicode[STIX]{x1D711}_{2}e^{i\unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D70F}-t)}\,\text{d}A^{\prime }\text{d}\unicode[STIX]{x1D70F}\right]\right.\nonumber\\ \displaystyle & & \displaystyle \times \left.\left.\unicode[STIX]{x1D711}_{1}\unicode[STIX]{x1D711}_{2}^{\ast }\,\text{d}A\vphantom{\left(\displaystyle \int _{\unicode[STIX]{x1D70F}=0}^{t}\displaystyle \int {\displaystyle \frac{1}{\unicode[STIX]{x1D705}}}G\unicode[STIX]{x1D711}_{1}\unicode[STIX]{x1D711}_{2}^{\ast }e^{-i\unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D70F}-t)}\,dA^{\prime }d\unicode[STIX]{x1D70F}\right)}\right\}\right\}\!,\quad\end{eqnarray}$$
where the gain saturation effect is included in the
![]() $g_{\text{sat}}$
, which is defined as[Reference Hansen and Lægsgaard15]
$g_{\text{sat}}$
, which is defined as[Reference Hansen and Lægsgaard15]
where
![]() $g_{0}$
is the small signal gain,
$g_{0}$
is the small signal gain,
![]() $P_{\text{sat}}$
is the saturation power, and
$P_{\text{sat}}$
is the saturation power, and
![]() $\unicode[STIX]{x1D6E4}_{1}$
and
$\unicode[STIX]{x1D6E4}_{1}$
and
![]() $P_{1}$
are the filling factor and power of the FM, respectively.
$P_{1}$
are the filling factor and power of the FM, respectively.
Similar to Ref. [Reference Tao, Su, Ma, Wang and Zhou17], we define the coupling coefficient as
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D712}(\unicode[STIX]{x1D6FA}) & = & \displaystyle 2\frac{i\unicode[STIX]{x1D702}\unicode[STIX]{x1D6FD}_{2}}{n_{0}}\left(\frac{\unicode[STIX]{x1D706}_{s}}{\unicode[STIX]{x1D706}_{p}}-1\right)\nonumber\\ \displaystyle & & \displaystyle \times \,\left\{\int \left[\int _{\unicode[STIX]{x1D70F}=0}^{t}\int \frac{1}{\unicode[STIX]{x1D705}}G\unicode[STIX]{x1D711}_{1}^{\ast }\unicode[STIX]{x1D711}_{2}e^{i\unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D70F}-t)}\,\text{d}A^{\prime }\text{d}\unicode[STIX]{x1D70F}\right]\right.\nonumber\\ \displaystyle & & \displaystyle \times \,\left.\unicode[STIX]{x1D711}_{1}\unicode[STIX]{x1D711}_{2}^{\ast }\,\text{d}A\vphantom{\left(\displaystyle \int _{\unicode[STIX]{x1D70F}=0}^{t}\displaystyle \int {\displaystyle \frac{1}{\unicode[STIX]{x1D705}}}G\unicode[STIX]{x1D711}_{1}\unicode[STIX]{x1D711}_{2}^{\ast }e^{-i\unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D70F}-t)}\,dA^{\prime }d\unicode[STIX]{x1D70F}\right)}\right\}\!.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D712}(\unicode[STIX]{x1D6FA}) & = & \displaystyle 2\frac{i\unicode[STIX]{x1D702}\unicode[STIX]{x1D6FD}_{2}}{n_{0}}\left(\frac{\unicode[STIX]{x1D706}_{s}}{\unicode[STIX]{x1D706}_{p}}-1\right)\nonumber\\ \displaystyle & & \displaystyle \times \,\left\{\int \left[\int _{\unicode[STIX]{x1D70F}=0}^{t}\int \frac{1}{\unicode[STIX]{x1D705}}G\unicode[STIX]{x1D711}_{1}^{\ast }\unicode[STIX]{x1D711}_{2}e^{i\unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D70F}-t)}\,\text{d}A^{\prime }\text{d}\unicode[STIX]{x1D70F}\right]\right.\nonumber\\ \displaystyle & & \displaystyle \times \,\left.\unicode[STIX]{x1D711}_{1}\unicode[STIX]{x1D711}_{2}^{\ast }\,\text{d}A\vphantom{\left(\displaystyle \int _{\unicode[STIX]{x1D70F}=0}^{t}\displaystyle \int {\displaystyle \frac{1}{\unicode[STIX]{x1D705}}}G\unicode[STIX]{x1D711}_{1}\unicode[STIX]{x1D711}_{2}^{\ast }e^{-i\unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D70F}-t)}\,dA^{\prime }d\unicode[STIX]{x1D70F}\right)}\right\}\!.\end{eqnarray}$$
According to Equation (12), the powers of the FM and HOM are as follows:
Substituting Equation (25) and Equation (26) into Equation (23) and re-writing the mode coupling equation in the form of the mode power, we obtain the improved coupled-mode equation that considers the thermally induced mode bending loss decrease and TMI:
 $$\begin{eqnarray}\begin{array}{@{}l@{}}{\displaystyle \frac{\unicode[STIX]{x2202}P_{1}}{\unicode[STIX]{x2202}z}}=\unicode[STIX]{x1D6E4}_{1}(Q_{p})gP_{1}-g_{\text{sat}}\unicode[STIX]{x1D712}(Q_{p})P_{2}P_{1}-2\unicode[STIX]{x1D6FC}_{1}(Q_{p})P_{1},\\ {\displaystyle \frac{\unicode[STIX]{x2202}P_{2}}{\unicode[STIX]{x2202}z}}=\unicode[STIX]{x1D6E4}_{2}(Q_{p})gP_{2}+g_{\text{sat}}\unicode[STIX]{x1D712}(Q_{p})P_{2}P_{1}-2\unicode[STIX]{x1D6FC}_{2}(Q_{p})P_{2}.\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}l@{}}{\displaystyle \frac{\unicode[STIX]{x2202}P_{1}}{\unicode[STIX]{x2202}z}}=\unicode[STIX]{x1D6E4}_{1}(Q_{p})gP_{1}-g_{\text{sat}}\unicode[STIX]{x1D712}(Q_{p})P_{2}P_{1}-2\unicode[STIX]{x1D6FC}_{1}(Q_{p})P_{1},\\ {\displaystyle \frac{\unicode[STIX]{x2202}P_{2}}{\unicode[STIX]{x2202}z}}=\unicode[STIX]{x1D6E4}_{2}(Q_{p})gP_{2}+g_{\text{sat}}\unicode[STIX]{x1D712}(Q_{p})P_{2}P_{1}-2\unicode[STIX]{x1D6FC}_{2}(Q_{p})P_{2}.\end{array}\end{eqnarray}$$
This equation is very straightforward that the first term on the RHS stands for the power amplification, the second term is the power coupling between FM and HOM due to the TMI, and the third term represents the power loss due to the fiber bending. It should be noted that the parameters such as filling factor, coupling coefficient and mode loss are now the functions of the heat load
![]() $Q_{p}$
and should be calculated along the active fiber.
$Q_{p}$
and should be calculated along the active fiber.
3 Numerical simulation of the TICLL in co-pumped step-index 20/400 fiber amplifier
Based on the improved coupled-mode equation, we simulate the TICLL in the co-pumped fiber amplifier based on conventional LMA 20/400 fiber. The core/cladding diameter is
![]() $20~\unicode[STIX]{x03BC}\text{m}/400~\unicode[STIX]{x03BC}\text{m}$
and the core/cladding numerical aperture (NA) is
$20~\unicode[STIX]{x03BC}\text{m}/400~\unicode[STIX]{x03BC}\text{m}$
and the core/cladding numerical aperture (NA) is
![]() $0.06/0.46$
, repectively. The fiber core supports fundamental mode and two HOMs:
$0.06/0.46$
, repectively. The fiber core supports fundamental mode and two HOMs:
![]() $\mathit{LP}_{11o}$
,
$\mathit{LP}_{11o}$
,
![]() $\mathit{LP}_{11e}$
, considering the polarization due to the fiber coiling. We only focus on the mode coupling between the FM and the
$\mathit{LP}_{11e}$
, considering the polarization due to the fiber coiling. We only focus on the mode coupling between the FM and the
![]() $\mathit{LP}_{11o}$
mode since TMI usually happens between FM and the nearest HOM[Reference Hansen, Alkeskjold, Broeng and Lægsgaard14]. Other parameters are listed in Table 1.
$\mathit{LP}_{11o}$
mode since TMI usually happens between FM and the nearest HOM[Reference Hansen, Alkeskjold, Broeng and Lægsgaard14]. Other parameters are listed in Table 1.
Table 1. Parameters of the LMA 20/400 fiber.

In order to solve the coupled-mode equations given by Equation (27), the pump power distribution along the active fiber as well as the signal gain is required. Therefore, we introduce the rate equation and the pump propagation equation as shown below:
 $$\begin{eqnarray}\begin{array}{@{}l@{}}N_{2}=N_{Yb} [\,(P_{p}^{+}+P_{p}^{-})\unicode[STIX]{x1D70E}_{p}^{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6E4}_{p}/h\unicode[STIX]{x1D710}_{p}A_{\text{clad}}\\ \qquad \;+\,(\unicode[STIX]{x1D6E4}_{1}P_{1}+\unicode[STIX]{x1D6E4}_{2}P_{2})\unicode[STIX]{x1D70E}_{s}^{\unicode[STIX]{x1D6FC}}/h\unicode[STIX]{x1D710}_{s}A_{\text{clad}}]/\\ \qquad \;[\,(P_{p}^{+}+P_{p}^{-})\times (\unicode[STIX]{x1D70E}_{p}^{\unicode[STIX]{x1D6FC}}+\unicode[STIX]{x1D70E}_{p}^{e})\times \unicode[STIX]{x1D6E4}_{p}/h\unicode[STIX]{x1D710}_{p}A_{\text{clad}}\\ \qquad \;+\,(\unicode[STIX]{x1D6E4}_{1}P_{1}+\unicode[STIX]{x1D6E4}_{2}P_{2})\times (\unicode[STIX]{x1D70E}_{s}^{\unicode[STIX]{x1D6FC}}+\unicode[STIX]{x1D70E}_{s}^{e})/h\unicode[STIX]{x1D710}_{s}A_{\text{clad}}+1/\unicode[STIX]{x1D70F}\!]^{-1},\\ {\displaystyle \frac{\text{d}\!P_{p}^{\pm }}{\text{d}z}}=\pm \unicode[STIX]{x1D6E4}_{p}P_{p}^{\pm }(\unicode[STIX]{x1D70E}_{p}^{e}N_{2}-\unicode[STIX]{x1D70E}_{p}^{\unicode[STIX]{x1D6FC}}N_{1}),\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}l@{}}N_{2}=N_{Yb} [\,(P_{p}^{+}+P_{p}^{-})\unicode[STIX]{x1D70E}_{p}^{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D6E4}_{p}/h\unicode[STIX]{x1D710}_{p}A_{\text{clad}}\\ \qquad \;+\,(\unicode[STIX]{x1D6E4}_{1}P_{1}+\unicode[STIX]{x1D6E4}_{2}P_{2})\unicode[STIX]{x1D70E}_{s}^{\unicode[STIX]{x1D6FC}}/h\unicode[STIX]{x1D710}_{s}A_{\text{clad}}]/\\ \qquad \;[\,(P_{p}^{+}+P_{p}^{-})\times (\unicode[STIX]{x1D70E}_{p}^{\unicode[STIX]{x1D6FC}}+\unicode[STIX]{x1D70E}_{p}^{e})\times \unicode[STIX]{x1D6E4}_{p}/h\unicode[STIX]{x1D710}_{p}A_{\text{clad}}\\ \qquad \;+\,(\unicode[STIX]{x1D6E4}_{1}P_{1}+\unicode[STIX]{x1D6E4}_{2}P_{2})\times (\unicode[STIX]{x1D70E}_{s}^{\unicode[STIX]{x1D6FC}}+\unicode[STIX]{x1D70E}_{s}^{e})/h\unicode[STIX]{x1D710}_{s}A_{\text{clad}}+1/\unicode[STIX]{x1D70F}\!]^{-1},\\ {\displaystyle \frac{\text{d}\!P_{p}^{\pm }}{\text{d}z}}=\pm \unicode[STIX]{x1D6E4}_{p}P_{p}^{\pm }(\unicode[STIX]{x1D70E}_{p}^{e}N_{2}-\unicode[STIX]{x1D70E}_{p}^{\unicode[STIX]{x1D6FC}}N_{1}),\end{array}\end{eqnarray}$$
where
![]() $A_{\text{clad}}$
is the area of the inner cladding,
$A_{\text{clad}}$
is the area of the inner cladding,
![]() $\unicode[STIX]{x1D70E}_{p}^{e}$
,
$\unicode[STIX]{x1D70E}_{p}^{e}$
,
![]() $\unicode[STIX]{x1D70E}_{p}^{a}$
and
$\unicode[STIX]{x1D70E}_{p}^{a}$
and
![]() $\unicode[STIX]{x1D6E4}_{p}$
are the emission/absorption cross section and filling factor for the pump light, respectively. The seed power consists of 10 W FM power and the pump power is increased gradually from 200 W to 2850 W. The TMI is assumed to be seeded by quantum noise. The total length of the active fiber used in our simulation is 14 m, which is coiled at the radius of 5 cm. The doping concentration is
$\unicode[STIX]{x1D6E4}_{p}$
are the emission/absorption cross section and filling factor for the pump light, respectively. The seed power consists of 10 W FM power and the pump power is increased gradually from 200 W to 2850 W. The TMI is assumed to be seeded by quantum noise. The total length of the active fiber used in our simulation is 14 m, which is coiled at the radius of 5 cm. The doping concentration is
![]() $5.58\times 10^{25}~\text{m}^{-3}$
, which corresponds to the absorption coefficient of
$5.58\times 10^{25}~\text{m}^{-3}$
, which corresponds to the absorption coefficient of
![]() $0.48~\text{dB}/\text{m}$
at 915 nm. Other parameters for the fiber amplifier are shown in Table 2.
$0.48~\text{dB}/\text{m}$
at 915 nm. Other parameters for the fiber amplifier are shown in Table 2.
Table 2. Parameters of the 20/400 amplifier.

Figure 1 shows the output power evolution and the power conversion efficiency (PCE) evolution with the pump power for the co-pumped 20/400 fiber amplifier. It can be seen that the TICLL is successfully reproduced in our simulation, the output power first increases monolithically when the pump power is less than 3300 W and then deceases dramatically when the pump power is further increased above 3300 W. Similarly, the PCE first increases and then decreases with the pump power as well. The maximum output power of 2856 W is obtained at 3300 W pump power, while the maximum PCE of 90.3% is achieved at 2800 W pump power.

Figure 1. Output power and PCE evolution of the co-pumped amplifier.
According to the peak value of the PCE and the output power, Figure 1 could be divided into three stages: (I) the pump power is below 2800 W, where both the PCE and the output power increase with the pump power, (II) the pump power is between 2800 W and 3300 W, where the PCE starts to decrease with the pump power while the output power increases slowly with the pump power, and (III) the pump power is above 3300 W and both the PCE and the output power decrease with the pump power. In order to provide a better insight into the output power evolution in these three stages, we plot the power distribution along the active fiber under three different pump powers, 2000, 3250, and 3400 W, as shown in Figures 2, 3 and 4, respectively.
For the first stage shown in Figure 2, only FM power is amplified, which also leads to the quasi-linear increase of the output power. No power coupling from FM to HOM happens, meaning that the signal power is still below the threshold of TMI. The increase of the PCE is due to the decrease of the FM loss, which is consistent with the result in Ref. [Reference Kong, Leng, Zhou and Jiang20]. For the second stage, a small fraction of FM power couples into the HOM power, as demonstrated in Figure 3. This indicates that the signal power is near the threshold of the TMI. Then the HOM power decreases in the rear section of the active fiber. This is the main reason for the decrease of the PCE. It should be mentioned that the output power is dominated by the FM power and the FM gain is stronger than the coupling from FM to the HOM. Therefore, the output power still increases with the pump power in the second stage. For the third stage shown in Figure 4, the TMI is triggered so that obvious power coupling from FM to HOM is observed. Similar to Figure 3, the HOM power also decreases dramatically in the rear section of the fiber. In this stage, the coupling from the FM to the HOM is stronger than the FM gain, which leads to the decrease of both the PCE and output power.

Figure 2. Power distribution in the co-pumped amplifier in the first stage.

Figure 3. Power distribution in the co-pumped amplifier in the second stage.

Figure 4. Power distribution in the co-pumped amplifier in the third stage.
The HOM power decrease is due to the thermally induced mode bending loss decrease along the active fiber. We plot the local heat load and HOM loss along the active fiber under 3000 W pump power, as shown in Figure 5. It could be seen that in the front section of the active fiber, the HOM loss becomes very small due to the excessive heat load. In the rear section of the fiber, the heat load decreases due to the pump power depletion and leads to the increase of the HOM loss. Large HOM bending loss will result in the leakage of the HOM power from the core to the inner cladding, which causes the HOM power decrease in the rear section of the active fiber. It should be noted that the HOM loss in Figure 5 is in the unit of dB
![]() $/$
m and must be transformed from the mode loss in Equation (2). Meanwhile, we also plot the coupling coefficient evolution along the active fiber, as demonstrated in Figure 6. It can be seen that the excessive heat load also leads to the increase of the coupling coefficient in the front section of the active fiber. The distribution of the coupling coefficient indicates that excessive heat load will not only lead to the decrease of the HOM loss but also the stronger coupling from the FM to the HOM.
$/$
m and must be transformed from the mode loss in Equation (2). Meanwhile, we also plot the coupling coefficient evolution along the active fiber, as demonstrated in Figure 6. It can be seen that the excessive heat load also leads to the increase of the coupling coefficient in the front section of the active fiber. The distribution of the coupling coefficient indicates that excessive heat load will not only lead to the decrease of the HOM loss but also the stronger coupling from the FM to the HOM.

Figure 5. Heat load and HOM loss distribution of the co-pumped fiber amplifier under 3000 W pump power.

Figure 6. Distribution of the mode coupling coefficient of the co-pumped fiber amplifier under 3000 W pump power.
To wrap up, the physical process of the core laser leakage could be summarized as follows: (I) the FM power reaches the threshold of TMI; (II) power coupling from FM to HOM happens in the front section of the active fiber; (III) HOM power leaks into the inner cladding due to the increase of the HOM loss in the rear section of the active fiber.
It should be noted that the TMI threshold in our simulation is much lower than that in Tao’s results, in which the output signal laser at TMI threshold is about 6.7 kW for the
![]() $20/400$
fiber amplifier under 5 cm bending radius. The reason for such significant threshold difference is due to the combined effect of the thermally induced bending mode loss decrease and the thermally induced mode coupling coefficient evolution. In Tao’s work, the mode loss is calculated via the Marcuse’s formula and the mode coupling coefficient is calculated based on the mode field of the straight fiber under zero heat load. Therefore the mode loss and the mode coupling coefficient are constant along the active fiber. In our model, the mode loss and mode field are first calculated according to the local refractive index profile via the FEM solver. Then the mode field is used to calculate the filling factor and the mode coupling coefficient. Thus the mode loss and the mode coupling coefficient are decided by the local refractive index, which depends on the local heat load. As discussed above, excessive heat load will lead to the decrease of the HOM loss and increase of the coupling coefficient, which further decrease the TMI threshold as a result. Thus the threshold calculated by our model is much lower than that in Ref. [Reference Tao, Su, Ma, Wang and Zhou17].
$20/400$
fiber amplifier under 5 cm bending radius. The reason for such significant threshold difference is due to the combined effect of the thermally induced bending mode loss decrease and the thermally induced mode coupling coefficient evolution. In Tao’s work, the mode loss is calculated via the Marcuse’s formula and the mode coupling coefficient is calculated based on the mode field of the straight fiber under zero heat load. Therefore the mode loss and the mode coupling coefficient are constant along the active fiber. In our model, the mode loss and mode field are first calculated according to the local refractive index profile via the FEM solver. Then the mode field is used to calculate the filling factor and the mode coupling coefficient. Thus the mode loss and the mode coupling coefficient are decided by the local refractive index, which depends on the local heat load. As discussed above, excessive heat load will lead to the decrease of the HOM loss and increase of the coupling coefficient, which further decrease the TMI threshold as a result. Thus the threshold calculated by our model is much lower than that in Ref. [Reference Tao, Su, Ma, Wang and Zhou17].

Figure 7. Comparison of the output power evolution with the pump power for the co-pumping scheme and counter-pumping scheme.
4 Discussion
In the above section, we have successfully reproduced the TICLL phenomenon in the co-pumped step-index
![]() $20/400$
fiber amplifier based on our improved coupled-mode equation. The TICLL effect is in fact a damage effect for the co-pumped fiber amplifier since this effect will generate large amount of cladding light, which may damage the cladding power stripper. Moreover, the TICLL effect is also related to the photodarkening effect[Reference Kong, Li, Leng, Wang, Zhou, Xu, Chen and Jiang22], which will greatly influence the long term stability of the higher power fiber amplifier. Therefore, a mitigating strategy is required.
$20/400$
fiber amplifier based on our improved coupled-mode equation. The TICLL effect is in fact a damage effect for the co-pumped fiber amplifier since this effect will generate large amount of cladding light, which may damage the cladding power stripper. Moreover, the TICLL effect is also related to the photodarkening effect[Reference Kong, Li, Leng, Wang, Zhou, Xu, Chen and Jiang22], which will greatly influence the long term stability of the higher power fiber amplifier. Therefore, a mitigating strategy is required.
In our previous work[Reference Kong, Leng, Zhou and Jiang20], we have demonstrated that the counter-pumping scheme shows much better HOM suppression than the co-pumping scheme. In Ref. [Reference Kong, Li, Leng, Wang, Zhou, Xu, Chen and Jiang22], photodarkening induced TICLL effect is mitigated via the counter-pumping amplifier. These works indicate that the counter-pumping scheme will mitigate the TICLL effect. Thus in this section, we will investigate the core laser leakage in the counter-pumping fiber amplifier based on our improved model. All parameters are the same as in the simulation in the previous section except the pump power is launched from the rear end of the active fiber.
Figure 7 shows comparison of the output power evolution for the co-pumping scheme and counter-pumping scheme. It can be seen that the output power increases linearly with the pump power and no power decrease is observed. This indicates that the TICLL could be mitigated via the counter-pumping scheme. In order to further explain this phenomenon, we plot the heat load and HOM loss distribution for the counter-pumping fiber amplifier in Figure 8. It can be seen that the HOM loss is very small in the rear section of the active fiber due to the excessive heat load. Since the HOM loss is small, the HOM power will be confined in the core rather than leakage into the inner cladding even if the HOM power is excited. This is also consistent with the refractive index (RI) profile at the output end of the ytterbium doped fiber (YDF) for both the co-pumping scheme and counter-pumping scheme. Figure 9 plots the RI profile of the output end of the active fiber under 3000 W pump power. The corresponding heat is
![]() $1.5~\text{W}/\text{m}$
and
$1.5~\text{W}/\text{m}$
and
![]() $86~\text{W}/\text{m}$
, respectively. The core NA of the YDF in the counter-pumping scheme is much higher than that in the co-pumping scheme. Larger NA indicates better confinement for the core mode which means smaller HOM loss. Thus the excited HOM will output from the rear end of the YDF.
$86~\text{W}/\text{m}$
, respectively. The core NA of the YDF in the counter-pumping scheme is much higher than that in the co-pumping scheme. Larger NA indicates better confinement for the core mode which means smaller HOM loss. Thus the excited HOM will output from the rear end of the YDF.

Figure 8. HOM loss and heat load distribution along the active fiber in the counter-pumping fiber amplifier under 3000 W pump power.

Figure 9. RI profile at the output end of the YDF under 3000 W pump power for the co-pumping scheme and counter-pumping scheme.
Besides, the TMI threshold of the counter-pumping scheme is also higher than the threshold of the co-pumping scheme due to the gain saturation effect[Reference Hansen and Lægsgaard15]. It should be noted that our simulation does not consider the stimulated Raman scattering effect, which may also result in the onset of the TMI[Reference Hejaz, Shayganmanesh, Rezaei-Nasirabad, Roohforouz, Azizi, Abedinajafi and Vatani27]. This will be improved in our future work. Nevertheless, the mode loss distribution and higher TMI threshold lead to the mitigation of the TICLL effect in the counter-pumping scheme.
It should be noted that the TICLL could also be mitigated by adopting larger bending radius. However this will also lead to the dramatical decrease of the TMI threshold. As demonstrated in Figure 10, the corresponding output power and pump power are 1209 W and 1351 W, respectively. which are much lower than the threshold in the case of 5 cm bending radius. It can be seen that TICLL is not triggered as the output power still shows a linear increase with the pump power even when the pump power is above the TMI threshold.

Figure 10. Output power and HOM ratio evolution with the pump power for 20 cm bending radius.
5 Conclusion
In this paper, we propose a novel model to explain the physical process of the TICLL effect in high power co-pumped YDF amplifier. Both the thermally induced mode bending loss decrease and the TMI in the coiled active fiber are considered. Based on this model, we successfully reproduce the core laser leakage in the co-pumped
![]() $20/400$
fiber amplifier. The result shows that the core laser leakage is a combined effect of the thermally induced mode bending loss decrease and TMI that the FM power couples into the HOM power due to HOM loss decrease and the TMI effect in the front section of the active fiber and then leaks into the inner cladding due to the recovery of the HOM loss in the rear section of the active fiber. Besides, we simulate the mode coupling in the counter-pumping scheme based on our model. The result shows that the core laser leakage is mitigated in the counter-pumping scheme.
$20/400$
fiber amplifier. The result shows that the core laser leakage is a combined effect of the thermally induced mode bending loss decrease and TMI that the FM power couples into the HOM power due to HOM loss decrease and the TMI effect in the front section of the active fiber and then leaks into the inner cladding due to the recovery of the HOM loss in the rear section of the active fiber. Besides, we simulate the mode coupling in the counter-pumping scheme based on our model. The result shows that the core laser leakage is mitigated in the counter-pumping scheme.
Acknowledgement
The authors thank the support of National Natural Science Foundation of China (NSFC) (No. 61605246).