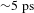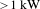1 Introduction
The continued advancement of compact, short pulse lasers with high average power is crucial for the development of important applications. These include driving the next generation of ultra-intense few-cycle and single-cycle sources at wavelengths ranging from the visible to the far infrared through optical parametric chirped pulse amplification (OPCPA)[Reference Fattahi, Barros, Gorjan, Nubbemeyer, Alsaif, Teisset, Schultze, Prinz, Haefner, Ueffing, Alismail, Vámos, Schwarz, Pronin, Brons, Geng, Arisholm, Ciappina, Yakovlev, Kim, Azzeer, Karpowicz, Sutter, Major, Metzger and Krausz1] and related schemes such as frequency-domain optical parametric amplification (FOPA)[Reference Schmidt, Thiré, Boivin, Laramée, Poitras, Lebrun, Ozaki, Ibrahim and Légaré2]. These lasers are also in demand for pumping tabletop secondary sources of radiation at more extreme wavelengths, such as drivers for coherent and incoherent sources of extreme ultraviolet (EUV), soft X-ray and hard X-rays[Reference Yin, Wang, Reagan, Baumgarten, Shlyaptsev, Bendik and Rocca3–Reference Alessi, Wang, Luther, Yin, Martz, Woolston, Liu, Berrill and Rocca8], and, at the opposite end of the spectrum, terahertz sources exploiting techniques like optical rectification[Reference Huang, Granados, Huang, Hong, Zapata and Kärtner9, Reference Oh, You, Jhajj, Rosenthal, Milchberg and Kim10]. These compact coherent, short wavelength sources can be realized through high harmonic generation[Reference Carstens, Högner, Saule, Holzberger, Lilienfein, Guggenmos, Jocher, Eidam, Esser, Tosa, Pervak, Limpert, Tünnermann, Kleineberg, Krausz and Pupeza5, Reference Popmintchev, Chen, Popmintchev, Arpin, Brown, Alisauskas, Andriukaitis, Balciunas, Mucke, Pugzlys, Baltuska, Shim, Schrauth, Gaeta, Hernandez-Garcia, Plaja, Becker, Jaron-Becker, Murnane and Kapteyn6] and plasma-based soft X-ray lasers[Reference Wang, Larotonda, Luther, Alessi, Berrill, Shlyaptsev and Rocca7, Reference Alessi, Wang, Luther, Yin, Martz, Woolston, Liu, Berrill and Rocca8]. In turn, the development of high power incoherent, plasma-based sources of EUV radiation is key to the advancement of lithography for the fabrication of the next generations of computer processors and memory[Reference Yin, Wang, Reagan, Baumgarten, Shlyaptsev, Bendik and Rocca3]. Furthermore, high flux beams of high energy picosecond pulses are of interest for the production of gamma rays through inverse Compton scattering with accelerated electron beams[Reference Gibson, Albert, Anderson, Betts, Messerly, Phan, Semenov, Shverdin, Tremaine, Hartemann, Siders, McNabb and Barty11, Reference Dupraz, Cassou, Delerue, Fichot, Martens, Stocchi, Variola, Zomer, Courjaud and Mottay12]. In addition, these lasers are of interest for the generation of high energy femtosecond laser pulses at very high repetition rates (multi-kilowatt-average powers) to enable the implementation of compact, practical particle accelerators based on laser wakefield acceleration[Reference Leemans, Gonsalves, Mao, Nakamura, Benedetti, Schroeder, Tóth, Daniels, Mittelberger, Bulanov, Vay, Geddes and Esarey13, Reference Wang, Zgadzaj, Fazel, Li, Yi, Zhang, Henderson, Chang, Korzekwa, Tsai, Pai, Quevedo, Dyer, Gaul, Martinez, Bernstein, Borger, Spinks, Donovan, Khudik, Shvets, Ditmire and Downer14], greatly increasing access to giga electron-volt beams for basic research and therapeutic radiation treatments. These and other applications are motivating the development of high average power, short pulse lasers by groups at institutions worldwide.

Figure 1. Summary of diode-pumped, high energy/high average power, short pulse lasers. Demonstrated, diode-pumped,
![]() $\unicode[STIX]{x1D706}\approx 1~\unicode[STIX]{x03BC}\text{m}$
lasers producing
$\unicode[STIX]{x1D706}\approx 1~\unicode[STIX]{x03BC}\text{m}$
lasers producing
![]() ${>}10~\text{mJ}$
pulse energy at
${>}10~\text{mJ}$
pulse energy at
![]() ${>}10~\text{Hz}$
repetition rate that are compressible to sub-10 ps duration are included. The energy scale is before compression, and the reference number of each laser is shown next to each.
${>}10~\text{Hz}$
repetition rate that are compressible to sub-10 ps duration are included. The energy scale is before compression, and the reference number of each laser is shown next to each.

Figure 2. (a) Laser system diagram. The output of a diode-pumped, mode-locked bulk Yb:KYW oscillator is stretched by a grating stretcher and amplified to the millijoule level by a Yb:YAG regenerative amplifier. These seed pulses are subsequently amplified by a chain of two high power cryogenic amplifiers, and are compressed in vacuum by a dielectric grating pair. (b) Panoramic photograph of the high energy, high average power laser.
Figure 1 summarizes the current state of the art of high energy, high average power, diode-pumped short pulse lasers[Reference Kawanaka, Yamakawa, Nishioka and Ueda15–Reference Curtis, Reagan, Wernsing, Furch, Luther and Rocca38]. Considerable progress has been made in the development of picosecond and femtosecond lasers with pulse energies of tens of millijoules to a few hundred millijoules at average powers approaching or exceeding 1 kW. These lasers have been enabled using various techniques. The thin disk geometry[Reference Giesen, Hügel, Voss, Wittig, Brauch and Opower39] was particularly successful, and was recently employed to generate
![]() ${>}$
200 mJ pulses at 5 kHz repetition rate and
${>}$
200 mJ pulses at 5 kHz repetition rate and
![]() ${>}$
100 mJ at 10 kHz repetition rate[Reference Fattahi, Alismail, Wang, Brons, Pronin, Buberl, Vámos, Arisholm, Azzeer and Krausz25]. Other schemes include the innoslab geometry[Reference Russbueldt, Mans, Rotarius, Weitenberg, Hoffmann and Poprawe40], which is recently demonstrated to produce
${>}$
100 mJ at 10 kHz repetition rate[Reference Fattahi, Alismail, Wang, Brons, Pronin, Buberl, Vámos, Arisholm, Azzeer and Krausz25]. Other schemes include the innoslab geometry[Reference Russbueldt, Mans, Rotarius, Weitenberg, Hoffmann and Poprawe40], which is recently demonstrated to produce
![]() ${>}$
50 mJ pulses at 10 kHz repetition rate[Reference Schmidt, Hage, Mans, Légaré and Wörner34], coherent beam combining of ultrafast fiber lasers[Reference Kienel, Müller, Klenke, Limpert and Tünnermann18, Reference Astrauskas, Kaksis, Flöry, Andriukaitis, Pugžlys, Baltuška, Ruppe, Chen, Galvanauskas and Balčiūnas41] and cryogenic cooling[Reference Kawanaka, Yamakawa, Nishioka and Ueda15, Reference Zapata, Lin, Calendron, Cankaya, Hemmer, Reichert, Huang, Granados, Hong and Kärtner21, Reference Morrissey, Fan, Miller and Rand33, Reference Rand, Miller, Ripin and Fan42]. These techniques have all been successful at generating moderate pulse energies with kilowatt-level average powers and are actively under development. Most of these lasers employ diode-pumped Yb:YAG as the active material due to its excellent average power-handling characteristics and broad availability. Lasers based on other materials which support a broader bandwidth, including Yb:YLF[Reference Kawanaka, Yamakawa, Nishioka and Ueda15, Reference Rand, Shaw, Ochoa, Ripin, Taylor, Fan, Martin, Hawes, Zhang, Sarkisyan, Wilson and Lundquist26, Reference Miller, Zapata, Ripin and Fan27], Yb:CaF
${>}$
50 mJ pulses at 10 kHz repetition rate[Reference Schmidt, Hage, Mans, Légaré and Wörner34], coherent beam combining of ultrafast fiber lasers[Reference Kienel, Müller, Klenke, Limpert and Tünnermann18, Reference Astrauskas, Kaksis, Flöry, Andriukaitis, Pugžlys, Baltuška, Ruppe, Chen, Galvanauskas and Balčiūnas41] and cryogenic cooling[Reference Kawanaka, Yamakawa, Nishioka and Ueda15, Reference Zapata, Lin, Calendron, Cankaya, Hemmer, Reichert, Huang, Granados, Hong and Kärtner21, Reference Morrissey, Fan, Miller and Rand33, Reference Rand, Miller, Ripin and Fan42]. These techniques have all been successful at generating moderate pulse energies with kilowatt-level average powers and are actively under development. Most of these lasers employ diode-pumped Yb:YAG as the active material due to its excellent average power-handling characteristics and broad availability. Lasers based on other materials which support a broader bandwidth, including Yb:YLF[Reference Kawanaka, Yamakawa, Nishioka and Ueda15, Reference Rand, Shaw, Ochoa, Ripin, Taylor, Fan, Martin, Hawes, Zhang, Sarkisyan, Wilson and Lundquist26, Reference Miller, Zapata, Ripin and Fan27], Yb:CaF
![]() $_{2}$
[Reference Siebold, Bock, Schramm, Xu, Doualan, Camy and Moncorgé43] and others are under development. Figure 1 also summarizes the progress in the development of kilowatt average short pulse lasers with pulse energies of
$_{2}$
[Reference Siebold, Bock, Schramm, Xu, Doualan, Camy and Moncorgé43] and others are under development. Figure 1 also summarizes the progress in the development of kilowatt average short pulse lasers with pulse energies of
![]() ${>}1~\text{J}$
that are in demand for tabletop X-ray and gamma ray sources and, with further scaling, will allow the development of practical compact giga electron-volt particle accelerators.
${>}1~\text{J}$
that are in demand for tabletop X-ray and gamma ray sources and, with further scaling, will allow the development of practical compact giga electron-volt particle accelerators.
In this paper, we describe a chirped pulse amplification (CPA) laser that produces 1 J pulses of picosecond duration at 0.5 kHz repetition rate with good long-term stability. We discuss new results of the characterization of this laser, including at-wavelength interferometry of the active region under thermal load, and we report initial results of operation of a 1 J amplifier operating at 1 kHz repetition rate, corresponding to 1 kW average power.
Our approach to generating high energy, picosecond duration pulses at high repetition rates relies on cryogenically cooled Yb:YAG active mirrors[Reference Reagan, Curtis, Wernsing, Furch, Luther and Rocca44]. Cryogenic cooling of Yb:YAG offers several advantages over room temperature operation. First, the thermal conductivity of undoped YAG is nearly an order of magnitude higher at liquid nitrogen boiling temperature than at room temperature[Reference Slack and Oliver45]. This enhancement is reduced when YAG is doped with a few percent Yb, but still offers a significant improvement of 3–5 times for moderate doping levels[Reference Aggarwal, Ripin, Ochoa and Fan46]. In addition, at this temperature, the thermal expansion coefficient and thermo-optic coefficient improve by factors of 4 and 7, respectively[Reference Aggarwal, Ripin, Ochoa and Fan46]. These enhancements are important as they largely determine the thermal refractive response of the material, which is often the effect that limits the achievable average power. In addition, the emission spectrum of Yb:YAG is narrower at 77 K, leading to an increase of the stimulated emission cross-section and the corresponding decrease of the saturation fluence[Reference Dong, Bass, Mao, Deng and Gan47]. This allows efficient energy extraction in a low number of passes at fluences which do not cause damage and do not lead to high nonlinear phase accumulation for the stretched pulse durations typically used in CPA systems. Furthermore, at cryogenic temperature, Yb-doped media function as four-level laser systems, as opposed to the quasi-three-level nature present at room temperature. This allows more efficient operation for high energy pulsed amplifiers.
The active mirror, thick disk geometry employed in our amplifiers develops mostly longitudinal thermal gradients which do not contribute to thermal lensing as strongly as the predominately radial gradients encountered in cylindrically cooled gain geometries. Its still comparatively small thickness, which minimizes the distance between heat generation and the cooling surface, limits the maximum temperature difference within the gain region while its moderate diameter to length ratio has the advantage of limiting the transverse gain, which diminishes amplified spontaneous emission (ASE) depletion of the amplifier storage energy[Reference Reagan, Curtis, Wernsing, Furch, Luther and Rocca44]. The improved thermal parameters at cryogenic temperatures compensates the larger thickness of this geometry compared to thin disk lasers (a few millimeter vs. a few hundred microns), with the additional advantage of increased pump absorption with reducing the complexity of the pump optics. Using this scheme, we have developed high energy CPA lasers that were used for a number of applications including the first demonstration of a diode-pumped, plasma-based soft X-ray laser[Reference Furch, Reagan, Luther, Curtis, Meehan and Rocca35],
![]() ${>}100~\unicode[STIX]{x03BC}\text{W}$
average power tabletop lasers at
${>}100~\unicode[STIX]{x03BC}\text{W}$
average power tabletop lasers at
![]() $\unicode[STIX]{x1D706}=18.9$
[Reference Reagan, Wernsing, Curtis, Furch, Luther, Patel, Menoni and Rocca48, Reference Reagan, Li, Urbanski, Wernsing, Salsbury, Baumgarten, Marconi, Menoni and Rocca49] and 13.9 nm[Reference Reagan, Berrill, Wernsing, Baumgarten, Woolston and Rocca50], Laser-induced damage threshold (LIDT) measurements of multilayer coatings[Reference Langston, Krous, Schiltz, Patel, Emmert, Markosyan, Reagan, Wernsing, Xu, Sun, Route, Fejer, Rocca, Rudolph and Menoni51], driving a 100 Hz repetition rate, millijoule energy OPCPA at
$\unicode[STIX]{x1D706}=18.9$
[Reference Reagan, Wernsing, Curtis, Furch, Luther, Patel, Menoni and Rocca48, Reference Reagan, Li, Urbanski, Wernsing, Salsbury, Baumgarten, Marconi, Menoni and Rocca49] and 13.9 nm[Reference Reagan, Berrill, Wernsing, Baumgarten, Woolston and Rocca50], Laser-induced damage threshold (LIDT) measurements of multilayer coatings[Reference Langston, Krous, Schiltz, Patel, Emmert, Markosyan, Reagan, Wernsing, Xu, Sun, Route, Fejer, Rocca, Rudolph and Menoni51], driving a 100 Hz repetition rate, millijoule energy OPCPA at
![]() $\unicode[STIX]{x1D706}=1.6~\unicode[STIX]{x03BC}\text{m}$
[Reference Schiltz, Patel, Baumgarten, Reagan, Rocca and Menoni52] and the characterization of the emission from a
$\unicode[STIX]{x1D706}=1.6~\unicode[STIX]{x03BC}\text{m}$
[Reference Schiltz, Patel, Baumgarten, Reagan, Rocca and Menoni52] and the characterization of the emission from a
![]() $\unicode[STIX]{x1D706}=6.x~\text{nm}$
laser produced plasma source for beyond EUV (BEUV) lithography[Reference Yin, Wang, Reagan, Baumgarten, Gullikson, Berrill, Shlyaptsev and Rocca53].
$\unicode[STIX]{x1D706}=6.x~\text{nm}$
laser produced plasma source for beyond EUV (BEUV) lithography[Reference Yin, Wang, Reagan, Baumgarten, Gullikson, Berrill, Shlyaptsev and Rocca53].

Figure 3. (a) Layout of the 500 Hz repetition rate, 100-mJ-level, cryogenic amplifier. (b) Measured pulse energy as a function of total pump energy at 500 Hz repetition rate. (c) Spectrum of the amplified pulses showing a bandwidth of 0.43 nm FWHM. (d) SHG autocorrelation of the compressed, 100 mJ pulses at 500 Hz repetition rate. The sech
![]() $^{2}$
fit shown corresponds to a pulse duration of 3.9 ps FWHM.
$^{2}$
fit shown corresponds to a pulse duration of 3.9 ps FWHM.
2 Laser description and results
2.1 Laser frontend
A block diagram showing the layout of the 500 Hz repetition rate, 1 J, picosecond laser system is shown in Figure 2(a). A semiconductor saturable absorber mirror (SESAM) mode-locked Yb:KYW oscillator produces
![]() ${\sim}20~\text{nJ}$
,
${\sim}20~\text{nJ}$
,
![]() ${\sim}300~\text{fs}$
pulses at 55 MHz repetition rate. These pulses are stretched by a folded, grating pulse stretcher to a duration of 270 ps FWHM after gain narrowing in the power amplifiers. The stretched pulses are amplified to
${\sim}300~\text{fs}$
pulses at 55 MHz repetition rate. These pulses are stretched by a folded, grating pulse stretcher to a duration of 270 ps FWHM after gain narrowing in the power amplifiers. The stretched pulses are amplified to
![]() ${\sim}1~\text{mJ}$
by a Yb:YAG active mirror regenerative amplifier. For the 500 Hz results summarized below, a Yb:YAG disk is soldered to a heat sink that is water-cooled at room temperature. For the 1 kHz operation we report here, the disk assembly was cooled by liquid nitrogen to 77 K. The millijoule-level pulses produced by the regenerative amplifier are temporally “cleaned” by a crossed calcite polarizer pair and Pockels cell before injection into the high power amplifier chain, which consists of the 100 mJ-level amplifier and a joule-level amplifier described below.
${\sim}1~\text{mJ}$
by a Yb:YAG active mirror regenerative amplifier. For the 500 Hz results summarized below, a Yb:YAG disk is soldered to a heat sink that is water-cooled at room temperature. For the 1 kHz operation we report here, the disk assembly was cooled by liquid nitrogen to 77 K. The millijoule-level pulses produced by the regenerative amplifier are temporally “cleaned” by a crossed calcite polarizer pair and Pockels cell before injection into the high power amplifier chain, which consists of the 100 mJ-level amplifier and a joule-level amplifier described below.

Figure 4. (a) Measured pulse energy exiting the 100-mJ-level cryogenic amplifier at 1 kHz repetition rate. (b) 30 min continuous operation at 1 kHz. A mean energy of 67 mJ with RMS fluctuation of 0.6% was measured over this 1.8 million consecutive shots.

Figure 5. (a) Layout of the high repetition rate, 1.5 J amplifier. (b) Photo of the enclosed amplifier, which occupies a table space of just over
![]() $1~\text{m}\times 0.5~\text{m}$
.
$1~\text{m}\times 0.5~\text{m}$
.
![]() $\unicode[STIX]{x1D706}/4$
: quarter waveplate, P: periscope, 6 kW: 60 bar laser diode stacks.
$\unicode[STIX]{x1D706}/4$
: quarter waveplate, P: periscope, 6 kW: 60 bar laser diode stacks.

Figure 6. (a) Measured laser pulse energy exiting the main amplifier at 500 Hz repetition rate as a function of combined pump energy. (b) Amplified pulse energy over 30 min of continuous operation at 500 Hz repetition rate. A mean energy of 1.4 J was measured with an RMS fluctuation of 0.75%. (c) M
![]() $^{2}$
measurement in two orthogonal directions of the amplified output producing 1.4 J at 500 Hz repetition rate. (d) Far-field beam image of the full power output.
$^{2}$
measurement in two orthogonal directions of the amplified output producing 1.4 J at 500 Hz repetition rate. (d) Far-field beam image of the full power output.
2.2 100-mJ-level amplifier
The layout of the 100-mJ-level amplifier is shown in Figure 3(a). A 5 mm thick, 2 at. % Yb:YAG active mirror is mounted on a cryogenic cooling manifold enclosed in a vacuum chamber. The highly reflective face of the active mirror is cooled by direct contact with flowing cryogenic liquid cooled to 77 K[Reference Baumgarten, Pedicone, Bravo, Wang, Yin, Menoni, Rocca and Reagan37]. The Yb:YAG active mirror is pumped by
![]() $\unicode[STIX]{x1D706}=940~\text{nm}$
,
$\unicode[STIX]{x1D706}=940~\text{nm}$
,
![]() $450~\unicode[STIX]{x03BC}\text{s}$
duration pulses produced by two, 400 W peak power fiber-coupled laser diode modules. A pump spot diameter of
$450~\unicode[STIX]{x03BC}\text{s}$
duration pulses produced by two, 400 W peak power fiber-coupled laser diode modules. A pump spot diameter of
![]() ${\sim}4~\text{mm}$
was used, and the pump radiation was absorbed in a single pass. We define a single pass as transmitting through the active region, reflecting from the back face, and passing back through active region before exiting the active mirror. The seed pulses from the laser frontend make four passes through the amplifier. Figure 3(b) shows the measured pulse energy exiting the amplifier as a function of total pump energy at 500 Hz repetition rate. As can be seen from this plot, an amplified pulse energy of 100 mJ (50 W average power) is obtained at the maximum pump energy. These pulses have a bandwidth of 0.43 nm FWHM [Figure 3(c)] and are compressed to sub-4 ps FWHM duration as can be seen by the second harmonic generation (SHG) autocorrelation of Figure 3(d). We have also operated this amplifier with a few modifications at higher repetition rates. For 1 kHz repetition rate amplification, the active mirror was replaced with a 2 mm thick, 3 at. % Yb:YAG active mirror, and an additional pass was added bringing the total pass number to 5. Figure 4(a) shows the amplified pulse energy at the output of this amplifier at 1 kHz repetition rate. Figure 4(b) shows an average energy of 67 mJ was measured with shot-to-shot energy fluctuations of 0.6% RMS over a continuous 30 min of operation (1.8 million shots).
${\sim}4~\text{mm}$
was used, and the pump radiation was absorbed in a single pass. We define a single pass as transmitting through the active region, reflecting from the back face, and passing back through active region before exiting the active mirror. The seed pulses from the laser frontend make four passes through the amplifier. Figure 3(b) shows the measured pulse energy exiting the amplifier as a function of total pump energy at 500 Hz repetition rate. As can be seen from this plot, an amplified pulse energy of 100 mJ (50 W average power) is obtained at the maximum pump energy. These pulses have a bandwidth of 0.43 nm FWHM [Figure 3(c)] and are compressed to sub-4 ps FWHM duration as can be seen by the second harmonic generation (SHG) autocorrelation of Figure 3(d). We have also operated this amplifier with a few modifications at higher repetition rates. For 1 kHz repetition rate amplification, the active mirror was replaced with a 2 mm thick, 3 at. % Yb:YAG active mirror, and an additional pass was added bringing the total pass number to 5. Figure 4(a) shows the amplified pulse energy at the output of this amplifier at 1 kHz repetition rate. Figure 4(b) shows an average energy of 67 mJ was measured with shot-to-shot energy fluctuations of 0.6% RMS over a continuous 30 min of operation (1.8 million shots).

Figure 7. (a) Schematic of the Mach–Zehnder interferometer used to make the thermal wavefront measurements. Millijoule-level,
![]() $\unicode[STIX]{x1D706}=1.03~\text{m}$
pulses produced by a Yb:YAG regenerative amplifier are magnified and beamsplit with equal magnitude. The probe arm is made to make a single pass through the Yb:YAG amplifier disk under test (where one pass is defined at transmitting through the active region of the active mirror, reflecting off the highly reflective (HR) face and transmitting again through the active region). The reference beam is sent through a delay line of length equal to the probe arm before the two beams are recombined by a second beamsplitter. An
$\unicode[STIX]{x1D706}=1.03~\text{m}$
pulses produced by a Yb:YAG regenerative amplifier are magnified and beamsplit with equal magnitude. The probe arm is made to make a single pass through the Yb:YAG amplifier disk under test (where one pass is defined at transmitting through the active region of the active mirror, reflecting off the highly reflective (HR) face and transmitting again through the active region). The reference beam is sent through a delay line of length equal to the probe arm before the two beams are recombined by a second beamsplitter. An
![]() $f=680~\text{mm}$
convex lens is used to image the plane of the amplifier onto a CMOS camera. The camera used in the interferometer is mounted on a translation stage that allows for precise determination of the location of the focus of the convex lens.
$f=680~\text{mm}$
convex lens is used to image the plane of the amplifier onto a CMOS camera. The camera used in the interferometer is mounted on a translation stage that allows for precise determination of the location of the focus of the convex lens.
2.3 High repetition rate, 1 J amplifier
The Joule-level amplifier is shown in Figure 5. Two Yb:YAG active mirrors are mounted on a single cryogenic cooling head. The active mirrors are composites, consisting of a
![]() $30~\text{mm}\times 30~\text{mm}\times 2~\text{mm}$
thick 3 at. % Yb:YAG section optically bonded on the four lateral faces to an absorbing Cr
$30~\text{mm}\times 30~\text{mm}\times 2~\text{mm}$
thick 3 at. % Yb:YAG section optically bonded on the four lateral faces to an absorbing Cr
![]() $^{4+}$
:YAG cladding to reduce feedback of transversely emitted ASE and avoid parasitic oscillations. The entire front face of the assembly is bonded to an undoped YAG cap to further reduce ASE and add mechanical stability to the assembly. As can be seen from Figure 5(a), each active mirror is pumped by pulses of
$^{4+}$
:YAG cladding to reduce feedback of transversely emitted ASE and avoid parasitic oscillations. The entire front face of the assembly is bonded to an undoped YAG cap to further reduce ASE and add mechanical stability to the assembly. As can be seen from Figure 5(a), each active mirror is pumped by pulses of
![]() $500~\unicode[STIX]{x03BC}\text{s}$
duration from a
$500~\unicode[STIX]{x03BC}\text{s}$
duration from a
![]() $\unicode[STIX]{x1D706}=940~\text{nm}$
60 bar laser diode stack. The pump beam diameter is
$\unicode[STIX]{x1D706}=940~\text{nm}$
60 bar laser diode stack. The pump beam diameter is
![]() ${\sim}16~\text{mm}$
, and the pump light is double-passed to achieve
${\sim}16~\text{mm}$
, and the pump light is double-passed to achieve
![]() ${>}$
95% absorption. Seed pulses are injected into the amplifier though a thin film polarizer (TFP) and are directed to pass through each active mirror twice. After double-passing a quarter waveplate the seed pulses pass back through the amplifier along the reverse path, achieving a total of four passes through each active mirror before being ejected from the amplifier by reflecting off the TFP. The amplifier occupies just over
${>}$
95% absorption. Seed pulses are injected into the amplifier though a thin film polarizer (TFP) and are directed to pass through each active mirror twice. After double-passing a quarter waveplate the seed pulses pass back through the amplifier along the reverse path, achieving a total of four passes through each active mirror before being ejected from the amplifier by reflecting off the TFP. The amplifier occupies just over
![]() $0.5~\text{m}^{2}$
of optical table area.
$0.5~\text{m}^{2}$
of optical table area.
3 High repetition rate, 1.5 J performance
The performance characteristics of this amplifier operating at 500 Hz repetition rate are shown in Figure 6. The laser output pulse energy as a function of total pump energy incident on the active mirrors is displayed in the plot of Figure 6(a). An output energy of 1.5 J (750 W average power) is obtained with an optical-to-optical efficiency of 37% at the maximum pump power. Figure 6(b) shows the measured output pulse energy stability over 30 min of continuous operation at 500 Hz repetition rate. A mean pulse energy of 1.4 J was obtained with an RMS deviation of 0.75%. Figure 6(c), shows the results of the measurement of the M
![]() $^{2}$
parameter under these same operating conditions. M
$^{2}$
parameter under these same operating conditions. M
![]() $^{2}$
values of about 1.3 are obtained on both axes. The second moment method was employed to make these measurements. The high beam quality can also be observed in the far-field image of Figure 6(d) along with its horizontal and vertical cuts. The output from this amplifier was collimated, and the beam was expanded to 40 mm before injection into the pulse compressor. The pulses were compressed with about 70% efficiency by a pair of
$^{2}$
values of about 1.3 are obtained on both axes. The second moment method was employed to make these measurements. The high beam quality can also be observed in the far-field image of Figure 6(d) along with its horizontal and vertical cuts. The output from this amplifier was collimated, and the beam was expanded to 40 mm before injection into the pulse compressor. The pulses were compressed with about 70% efficiency by a pair of
![]() $200~\text{mm}\times 150~\text{mm}$
,
$200~\text{mm}\times 150~\text{mm}$
,
![]() $1740~\text{mm}^{-1}$
dielectric diffraction gratings in vacuum. The resulting pulses had an energy of 1 J and a duration of
$1740~\text{mm}^{-1}$
dielectric diffraction gratings in vacuum. The resulting pulses had an energy of 1 J and a duration of
![]() ${\sim}5~\text{ps}$
at 500 Hz repetition rate, corresponding to a peak power of 0.2 TW and an average power of 0.5 kW. This laser was employed to make a first demonstration of a
${\sim}5~\text{ps}$
at 500 Hz repetition rate, corresponding to a peak power of 0.2 TW and an average power of 0.5 kW. This laser was employed to make a first demonstration of a
![]() ${>}100~\text{Hz}$
repetition rate, compact, plasma-based sub-20 nm soft X-ray laser[Reference Baumgarten, Pedicone, Bravo, Wang, Yin, Menoni, Rocca and Reagan37].
${>}100~\text{Hz}$
repetition rate, compact, plasma-based sub-20 nm soft X-ray laser[Reference Baumgarten, Pedicone, Bravo, Wang, Yin, Menoni, Rocca and Reagan37].
4 Interferometry of high energy active mirror amplifier
To further characterize these amplifiers at the pumping conditions corresponding to kilowatt average power operation and for evaluating their potential for future power scaling, we have made at-wavelength interferometric measurements of the gain medium deformation under full thermal load. Figure 7 shows the layout of the Mach–Zehnder interferometer that was constructed for these measurements. The
![]() $\unicode[STIX]{x1D706}=1030~\text{nm}$
output of the regenerative amplifier was used to record the interferograms. The results are shown in Figure 8. Figures 8(a)–8(d) show the interferograms obtained for average pump powers of 0.63, 0.70, 1.04, and 1.53 kW, respectively. The 1.04 kW interferogram [Figure 8(c)] corresponds to the pump power used in the 1.5 J, 500 Hz repetition rate demonstration described in the previous section. The amplifier was pumped, but no laser energy was extracted for these measurements. Operation of the amplifier with energy extraction is expected to decrease the overall thermal load. One feature to notice in this measurement is that the thermally induced wavefront partially compensates the static deformation present in the interferometer. Figures 8(e)–8(h) and 8(i)–8(l) show the wavefront profiles determined from these interferograms for different thermal load conditions. For these wavefront maps, the reference wavefront obtained with zero pump power is subtracted leaving only the thermal contribution. From these maps, we see that the thermal degradation of the wavefront for 0.63 kW average pump power is insignificant. The deformation increases to just over one wavelength at 1.53 kW, the highest pump power measured.
$\unicode[STIX]{x1D706}=1030~\text{nm}$
output of the regenerative amplifier was used to record the interferograms. The results are shown in Figure 8. Figures 8(a)–8(d) show the interferograms obtained for average pump powers of 0.63, 0.70, 1.04, and 1.53 kW, respectively. The 1.04 kW interferogram [Figure 8(c)] corresponds to the pump power used in the 1.5 J, 500 Hz repetition rate demonstration described in the previous section. The amplifier was pumped, but no laser energy was extracted for these measurements. Operation of the amplifier with energy extraction is expected to decrease the overall thermal load. One feature to notice in this measurement is that the thermally induced wavefront partially compensates the static deformation present in the interferometer. Figures 8(e)–8(h) and 8(i)–8(l) show the wavefront profiles determined from these interferograms for different thermal load conditions. For these wavefront maps, the reference wavefront obtained with zero pump power is subtracted leaving only the thermal contribution. From these maps, we see that the thermal degradation of the wavefront for 0.63 kW average pump power is insignificant. The deformation increases to just over one wavelength at 1.53 kW, the highest pump power measured.

Figure 8. Interferograms obtained for average pump power of (a) 0.63, (b) 0.70, (c) 1.04, and (d) 1.53 kW, respectively. (e–h) Calculated thermally deformed wavefront maps from these interferograms. A reference wavefront measured with no pump power was subtracted in each case, resulting in only the thermal contribution. All maps are plotted on the same scale. (i–l) 3D surface plots of the wavefronts.

Figure 9. Thermal focusing power as a function of average pump power calculated from the interferograms of Figure 8 (circles). Also shown are the thermal lens strengths measured from the displacement of the focus (squares). Straight lines connect successive points to guide the eye. At the highest thermal load, positive focal lengths of 30 and 41 m are obtained for the horizontal and vertical axes, respectively.
The thermal lens power obtained from these wavefronts is plotted in Figure 9. These powers were obtained by fitting an ellipsoid to the wavefronts, with the resulting horizontal and vertical radii constituting the thermal lens focal length. These interferometrically determined focal lengths were verified by measuring the focal length shift obtained by focusing a probe beam with a known positive lens. These latter values are shown to be in reasonable agreement with the data extracted from the interferograms, as shown in Figure 9. As can be seen from this figure, the thermal lens is positive, and increases approximately linearly with pump power for the lower pump powers. A rollover in optical power is observed at the highest pump powers, which is beneficial. This rollover may be due to contributions to the wavefront from heating of the anti-ASE absorbing cladding surrounding the Yb:YAG active mirror, but this requires further study. At the highest pump powers, focal lengths of 30 and 41 m are obtained. The astigmatism observed is partially a result of the angle of incidence of the probe beam on the amplifier disk of about
![]() ${\sim}10^{\circ }$
. This level of thermal lensing, while not negligible, is within the range that can be effectively compensated by adjusting the collimation of telescopes before and after the amplifier. It is concluded that at thermally induced wavefront deformation is not an impediment for scaling to the kilowatt average power level.
${\sim}10^{\circ }$
. This level of thermal lensing, while not negligible, is within the range that can be effectively compensated by adjusting the collimation of telescopes before and after the amplifier. It is concluded that at thermally induced wavefront deformation is not an impediment for scaling to the kilowatt average power level.

Figure 10. Measured amplified pulse energy at 1 kHz repetition rate as a function of total pump energy. The pump pulse duration was 0.5 ms, and the amplifier was seeded with about 65 mJ pulses (see Figure 4). At the maximum pump energy, an amplified pulse energy of 1 J was obtained with 25% optical-to-optical efficiency.
5 Initial demonstration of 1 J, 1 kHz repetition rate operation
In progress toward scaling this amplifier to higher repetition rates and average powers, we have made an initial demonstration of laser operation at 1 J and 1 kHz repetition rate (1 kW average power). This first test at the kilowatt average power level was conducted by seeding the high power amplifier with the 67 mJ pulses from the 1 kHz amplifier described above, and pumping the amplifier with the same pump pulses as before, but at an increased repetition rate of 1 kHz. The geometry of the joule-level, multi-pass amplifier remained the same. The results of this demonstration are shown in Figure 10. With a combined pump pulse energy of 4 J, an amplified pulse energy of 1 J was produced. In this initial demonstration, the amplifier was operated for short periods of time. Improved thermal management of the mechanical layout will be implemented to avoid misalignment of the beam during long term operation at 1 kW average power.
6 Summary
In summary, we have developed a CPA laser based on cryogenically cooled Yb:YAG active mirror amplifiers that produces 1 J, picosecond duration pulses at 500 Hz repetition rate with a measured RMS pulse to pulse energy variation of 0.75% over 30 min of operation. The amplifiers are modular and scalable. Interferometric measurements of the thermal lens show that this approach is suitable for the generation of beams of joule-level energy ultrashort laser pulses with kilowatt average power. We have made an initial demonstration of operation at 1 kW average power (1 J pulses at 1 kHz repetition rate).
Acknowledgements
The characterization of the cryogenically cooled high energy amplifier was supported by the U.S. Department of Energy Accelerator Stewardship programme, Office of High Energy Physics, Office of Science under award DE-SC0016136. The laser amplifier was developed with support by the U.S. Department of Energy, Office of Science SBIR programme under award DE-SC0011375.