No CrossRef data available.
Published online by Cambridge University Press: 12 April 2016
The main steps of the non-linear theory of spiral structure are described. Near each of the main resonances the basic periodic orbits are calculated, and the sets of non-periodic orbits that follow them are found. A different integral of motion is applicable for each set, besides the Jacobi integral. Then the initial distribution function, f, is expressed as a function of the two integrals and the corresponding angles. The final distribution function is found by averaging over the angles: 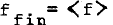 Then by integrating
Then by integrating 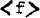 over all velocities we find the response density σresp. In order that σresp should be equal to the imposed density, σimp we must adjust the parameters of the imposed spiral field. The form of σresp away from resonances can be derived explicitely for tight ana open spirals or bars; however near the resonances σresp can be only calculated numerically. If the imposed field has almost constant amplitude, then the amplitude of the response is very large near the Inner Lindblad Resonance. In the case of a tight spiral the azimuth of the response density maximum with respect to the imposed density maximum tends to zero outside the ILR, while it tends to -90° inside the ILR. One possible self-consistent solution has zero amplitude inside the ILR both in the case of tight spirals and of bars. Finally an important quadrupole term was found near the ILR.
over all velocities we find the response density σresp. In order that σresp should be equal to the imposed density, σimp we must adjust the parameters of the imposed spiral field. The form of σresp away from resonances can be derived explicitely for tight ana open spirals or bars; however near the resonances σresp can be only calculated numerically. If the imposed field has almost constant amplitude, then the amplitude of the response is very large near the Inner Lindblad Resonance. In the case of a tight spiral the azimuth of the response density maximum with respect to the imposed density maximum tends to zero outside the ILR, while it tends to -90° inside the ILR. One possible self-consistent solution has zero amplitude inside the ILR both in the case of tight spirals and of bars. Finally an important quadrupole term was found near the ILR.