No CrossRef data available.
Published online by Cambridge University Press: 12 April 2016
We consider here the spin—orbit coupling influence on the relative orbital motion of two bodies interacting gravitationally. We assume that one of the bodies is spherically symmetric and the other possesses a plane of dynamical symmetry. In the full non-linear settings, this problem permits coplanar motion when the mass center of the spherically symmetric body moves in the plane. We used this simple model for a qualitative estimation of the changes of the relative orbit in two cases: A) the Sun-asteroid case (the fast rotating rigid body), B) a small satellite of a big planet in resonant rotation.
The motion is described in the rigid body fixed frame. An appropriate change of physical units (Goźdiewski,1998a) leads to nondimensional dynamical variables and parameters. After that the Hamiltonian of the problem, written in polar variables, is the following
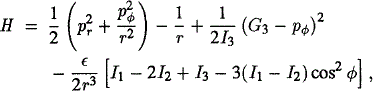
where (I1, I2, I3) are the principal moments of inertia, (r, φ) are the relative polar coordinates of the point mass in the body frame, (Pr, pφ) are the canonical momenta, (G3 represents the constant of total angular momentum, ε = (ro/r)2, and ro is the mean radius of the body.