Article contents
Planetary geodynamics and age constraints on circumstellar habitable zones around main sequence stars
Published online by Cambridge University Press: 14 March 2023
Abstract
Planetary geodynamics may have an important influence over planetary habitability and the boundaries of the circumstellar habitable zone (CHZ) in space and time. To investigate this we use a minimal parameterized model of the co-evolution of the geosphere and atmosphere of Earth-like planets around F, G, K and M main sequence stars. We found the CHZ for the present Solar System located between 0.92 and 1.09 au for a 1.0 M$_{\oplus }$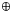 Earth-like planet, extendible to 1.36 au for a 4.0 M$_{\oplus }$
Earth-like planet, extendible to 1.36 au for a 4.0 M$_{\oplus }$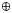 planet. In the literature, the CHZ varies considerably in width and border location, but the outer edges tend to be more spread out than the inner edges, showing a higher difficulty in determining the outer edge. Planetary mass has a considerable effect on planetary geodynamics, with low-mass planets cooling down faster and being less capable of maintaining a rich carbon dioxide atmosphere for several billions of years. Age plays a particularly important role in the width of the CHZ as the CHZ contracts in both directions: from the inner edge (as stellar luminosity increases with time), and from the outer edge (as planetary heat flux and seafloor spreading rate decrease with time). This strongly affects long-lived habitability as the 5 Gyr continuous CHZ may be very narrow or even non-existent for low-mass planets (<0.5 M$_{\oplus }$
planet. In the literature, the CHZ varies considerably in width and border location, but the outer edges tend to be more spread out than the inner edges, showing a higher difficulty in determining the outer edge. Planetary mass has a considerable effect on planetary geodynamics, with low-mass planets cooling down faster and being less capable of maintaining a rich carbon dioxide atmosphere for several billions of years. Age plays a particularly important role in the width of the CHZ as the CHZ contracts in both directions: from the inner edge (as stellar luminosity increases with time), and from the outer edge (as planetary heat flux and seafloor spreading rate decrease with time). This strongly affects long-lived habitability as the 5 Gyr continuous CHZ may be very narrow or even non-existent for low-mass planets (<0.5 M$_{\oplus }$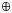 ) and fast-evolving high-mass stars (>1.1 M$_{\odot }$
) and fast-evolving high-mass stars (>1.1 M$_{\odot }$ ). Because of this, the mean age of habitable terrestrial planets in our Galaxy today may be younger than Earth's age. Our results suggest that the best targets for future surveys of biosphere signatures may be planets between 0.5 and 4.0 M$_{\oplus }$
). Because of this, the mean age of habitable terrestrial planets in our Galaxy today may be younger than Earth's age. Our results suggest that the best targets for future surveys of biosphere signatures may be planets between 0.5 and 4.0 M$_{\oplus }$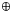 , in systems younger than the Solar System. These planets may present the widest and long-lived CHZ.
, in systems younger than the Solar System. These planets may present the widest and long-lived CHZ.
- Type
- Research Article
- Information
- Copyright
- Copyright © The Author(s), 2023. Published by Cambridge University Press
References
A correction has been issued for this article:
- 2
- Cited by
Linked content
Please note a has been issued for this article.



