Article contents
Least-squares fitting with errors in the response andpredictor
Published online by Cambridge University Press: 14 November 2012
Abstract
Least squares regression is commonly used in metrology for calibration and estimation. Inregression relating a response y to a predictor x, thepredictor x is often measured with error that is ignored in analysis.Practitioners wondering how to proceed when x has non-negligible errorface a daunting literature, with a wide range of notation, assumptions, and approaches.For the model ytrue = β0 + β1 xtrue,we provide simple expressions for errors in predictors (EIP) estimators \hbox{$\Hat{{\beta }}_{0, {\rm EIP}} $}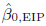 β̂0, EIP for β0 and \hbox{$\Hat{{\beta }}_{1, {\rm EIP}} $}
β̂0, EIP for β0 and \hbox{$\Hat{{\beta }}_{1, {\rm EIP}} $}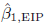 β̂1, EIP for β1 and for anapproximation to covariance (\hbox{$\Hat{{\beta }}_{0, {\rm EIP}} $}
β̂1, EIP for β1 and for anapproximation to covariance (\hbox{$\Hat{{\beta }}_{0, {\rm EIP}} $}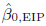 β̂0, EIP, \hbox{$\Hat{{\beta }}_{1, {\rm EIP}} $}
β̂0, EIP, \hbox{$\Hat{{\beta }}_{1, {\rm EIP}} $}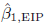 β̂1, EIP). It is assumed that there are measured datax = xtrue + ex,andy = ytrue + eywith errors ex in x andey in y and thevariances of the errors ex andey are allowed to depend onxtrue and ytrue, respectively.This paper also investigates the accuracy of the estimated cov(\hbox{$\Hat{{\beta }}_{0, {\rm EIP}} $}
β̂1, EIP). It is assumed that there are measured datax = xtrue + ex,andy = ytrue + eywith errors ex in x andey in y and thevariances of the errors ex andey are allowed to depend onxtrue and ytrue, respectively.This paper also investigates the accuracy of the estimated cov(\hbox{$\Hat{{\beta }}_{0, {\rm EIP}} $}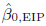 β̂0, EIP, \hbox{$\Hat{{\beta }}_{1, {\rm EIP}} $}
β̂0, EIP, \hbox{$\Hat{{\beta }}_{1, {\rm EIP}} $}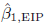 β̂1, EIP) and provides a numerical Bayesian alternative usingMarkov Chain Monte Carlo, which is recommended particularly for small sample sizes wherethe approximate expression is shown to have lower accuracy than desired.
β̂1, EIP) and provides a numerical Bayesian alternative usingMarkov Chain Monte Carlo, which is recommended particularly for small sample sizes wherethe approximate expression is shown to have lower accuracy than desired.
Information
- Type
- Research Article
- Information
- International Journal of Metrology and Quality Engineering , Volume 3 , Issue 2 , 2012 , pp. 117 - 123
- Copyright
- © EDP Sciences 2012
References
- 8
- Cited by

