Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-28T01:43:58.115Z Has data issue: false hasContentIssue false
  • English
  • Français

Least-squares fitting with errors in the response andpredictor

Published online by Cambridge University Press:  14 November 2012

T. Burr ,
S. Croft  and
B.C. Reed
T. Burr*
Affiliation:
Statistical Sciences, Los Alamos National Laboratory, USA
S. Croft
Affiliation:
Safeguards Science and Technology, Los Alamos National Laboratory, USA
B.C. Reed
Affiliation:
Department of Physics, Alma College, USA
*
⋆ Correspondence:tburr@lanl.gov
Get access

Abstract

Least squares regression is commonly used in metrology for calibration and estimation. Inregression relating a response y to a predictor x, thepredictor x is often measured with error that is ignored in analysis.Practitioners wondering how to proceed when x has non-negligible errorface a daunting literature, with a wide range of notation, assumptions, and approaches.For the model ytrue = β0 + β1   xtrue,we provide simple expressions for errors in predictors (EIP) estimators \hbox{$\Hat{{\beta }}_{0, {\rm EIP}} $}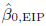β̂0, EIP for β0 and \hbox{$\Hat{{\beta }}_{1, {\rm EIP}} $}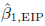β̂1, EIP for β1 and for anapproximation to covariance (\hbox{$\Hat{{\beta }}_{0, {\rm EIP}} $}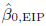β̂0, EIP, \hbox{$\Hat{{\beta }}_{1, {\rm EIP}} $}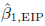β̂1, EIP). It is assumed that there are measured datax = xtrue + ex,andy = ytrue + eywith errors ex in x andey in y and thevariances of the errors ex andey are allowed to depend onxtrue and ytrue, respectively.This paper also investigates the accuracy of the estimated cov(\hbox{$\Hat{{\beta }}_{0, {\rm EIP}} $}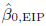β̂0, EIP, \hbox{$\Hat{{\beta }}_{1, {\rm EIP}} $}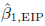β̂1, EIP) and provides a numerical Bayesian alternative usingMarkov Chain Monte Carlo, which is recommended particularly for small sample sizes wherethe approximate expression is shown to have lower accuracy than desired.

Keywords

Least squareregressionBayesian estimationerrors
Type
Research Article
Information
International Journal of Metrology and Quality Engineering , Volume 3 , Issue 2 , 2012 , pp. 117 - 123
Copyright
© EDP Sciences 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

R. Carroll, D. Ruppert, L. Stefanski, C. Crainiceanu, Measurement Error in Nonlinear Models (Chapman & Hall, 2006)
W. Deming, Statistical Adjustment of Data (Wiley, 1943)
W. Fuller, Measurement Error Models (Wiley, 1987)
Reed, B., A spreadsheet for linear least-squares fitting with errors in both coordinates, Phys. Educ. 45, 93–95 (2010) CrossRefGoogle Scholar
Reed, B., Linear least-squares fits with errors in both coordinates. II : Comments on parameter variances, Am. J. Phys. 60, 59–62 (1992) CrossRefGoogle Scholar
York, D., Evensen, N., Martinez, M., Delgado, J., Unified equations for the slope, intercept, and standard errors of the best straight line, Am. J. Phys. 72, 367–375 (2004) CrossRefGoogle Scholar
Wang, C., Iyer, H., Fiducial approach for assessing agreement between two instruments, Metrologia 45, 415–421 (2008) CrossRefGoogle Scholar
Brown, M., Robust line estimation with errors in both variables, J. Am. Stat. Assoc. 77, 71–79 (1982) CrossRefGoogle Scholar
Madansky, A., The fitting of straight lines when both variables are subject to errors, J. Am. Stat. Assoc. 54, 173–205 (1959) CrossRefGoogle Scholar
W. Press, S. Teukolsky, W. Vettterling, B. Flannery, Numerical Recipes, The Art of Scientific Computing, 3rd edn. (Cambridge University Press, 2007)
Toivanen, J., Dobaczewski, J., Kortelainen, M., Mizuyama, K., Error analysis of nuclear mass fits, Phys. Rev. C 78, 0343061–0343068 (2008) CrossRefGoogle Scholar
R Development Core Team 2004 R : A Language and Environment for Statistical Computing
Burr, T., Knepper, P., A study of the effect of measurement error in predictor variables in nondestructive assay, Appl. Radiat. Isotopes 53, 547–555 (2000) CrossRefGoogle ScholarPubMed
Elster, C., Toman, B., Bayesian uncertainty analysis for a regression model versus application of GUM supplement 1 to the least-squares estimate, Metrologia 48, 233–240 (2011) CrossRefGoogle Scholar
W. Gilks, S. Richardson, D. Spiegelhalter, Markov Chain Monte Carlo in Practice (Chapman & Hall/CRC, 1996)
Dellaportas, P., Stephens, D., Bayesian analysis of errors-in-variables regression models, Biometrics 51, 1085–1095 (1995) CrossRefGoogle Scholar
Kulathinal, S., Kuulasmaa, K., Gasbarra, D., Estimation of an errors-in-variables regression model with the variance of the measurement errors vary between the observations, Stat. Med. 21, 1089–1101 (2002) CrossRefGoogle ScholarPubMed
M. DeGroot, Probability and Statistics, 2nd edn. (Addison-Wesley, 1986)