Highly miniaturized wideband angular stable linear–circular and linear–cross polarization converter for Ka-band satellite applications
Published online by Cambridge University Press: 03 May 2023
Abstract
This work proposes a novel, extremely miniaturized wideband linear–circular and linear–cross metasurface-enabled reflective polarizer. This design comprises a Meander-line structure with horizontal dipoles as the top frequency selective surface, printed on a 1 mm thin-grounded FR-4 substrate. The x/y-polarized incident electromagnetic wave is converted as circularly polarized from 10.60 to 10.92 GHz (LHCP/RHCP), 12.12 to 17.32 GHz (RHCP/LHCP), and 22.72 to 37.76 GHz (LHCP/RHCP) during reflection with 2.97, 35.33, and 49.74% Fractional Bandwidth (FBW). In addition, this design shows linear–cross conversion with a minimum 90% polarization conversion ratio from 11.41 to 12, 19.01 to 22.34, and 40.74 to 46.82 GHz with an FBW of 5.04, 16.11, and 13.89%. The device performance is considerably stable under different oblique incidences, and the polarizer's unitcell is compact with a structural periodicity of 0.089 × 0.064 $\lambda _L^2$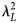 , and ultra-thin low-profile substrate thickness of 0.035λL. The proposed prototype is fabricated, and the measured results are in good agreement with the simulated one. This article also mentions how this polarizer could be tuned for dual-band K- and Ka-band satellite applications. The authors believe that the design's novelty lies in the multiband conversion with circular-polarization orthogonality, a highly miniaturized unitcell's volume of 0.199 $\lambda _L^3$
, and ultra-thin low-profile substrate thickness of 0.035λL. The proposed prototype is fabricated, and the measured results are in good agreement with the simulated one. This article also mentions how this polarizer could be tuned for dual-band K- and Ka-band satellite applications. The authors believe that the design's novelty lies in the multiband conversion with circular-polarization orthogonality, a highly miniaturized unitcell's volume of 0.199 $\lambda _L^3$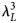 /1000, and better angular stability made this design a potential candidate for real-time satellite applications.
/1000, and better angular stability made this design a potential candidate for real-time satellite applications.
Information
- Type
- Metamaterials andPhotonic Bandgap Structures
- Information
- International Journal of Microwave and Wireless Technologies , Volume 15 , Issue 9 , November 2023 , pp. 1557 - 1569
- Copyright
- Copyright © Indian Institute of Technology Palakkad, 2023. Published by Cambridge University Press in association with the European Microwave Association
References
- 5
- Cited by


