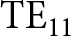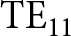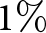Introduction
This paper is a continuation of the version presented at the Swedish Microwave Days (SMWD) conference and provides further results and discussion regarding the relativistic magnetron (RM) with a transparent cathode configuration [Reference Sawert, Vallejos, Nyberg, Hurtig and Dancila1].
The RM is a device that generates high-power microwaves (HPM), i.e., microwaves with radiation power exceeding ∼100 MW for frequencies of 1 GHz up to ∼10 GHz [Reference Benford, Swegle and Schamiloglu2–Reference Benford4]. This is achieved by applying high voltages over the anode-cathode (A-K) gap, which causes explosive emission of electrons from the emitter material disposed on the cathode. Furthermore, by applying an axial magnetic field over the interaction region, the electrons will start to gyrate in the A-K gap and drift in the azimuthal direction as a result of the relativistic Lorentz force. Slow-wave structures (SWS) in the form of cavities in the anode slow down the azimuthal phase velocity of the microwaves in order for them to match the velocity of the electrons. Consequently, electron-wave interaction occurs, enabling the transfer of electron kinetic energy to electromagnetic energy [Reference Benford, Swegle and Schamiloglu2].
The electron-wave interaction is greatly influenced by the applied voltage and magnetic field. As a result, different electromagnetic modes can be excited, depending on the exact values of the voltage and magnetic field. Previous research on RMs with six cavities (commonly referred to as A6 magnetrons) has shown favorable performance for the ![]() $2\pi/3$, π, and 2π modes [Reference Palevsky and Bekefi5–Reference Li and Liu12]. In this work, we will focus on exciting the π mode only, as this mode has been shown to yield good performance.
$2\pi/3$, π, and 2π modes [Reference Palevsky and Bekefi5–Reference Li and Liu12]. In this work, we will focus on exciting the π mode only, as this mode has been shown to yield good performance.
RMs that extract microwaves in the axial direction use a diffraction output structure that has the shape of an inverted cone with cavities (see Fig. 1). The role of the diffraction output is to extract the microwaves with high efficiency and to convert the radiation into a suitable mode in the cylindrical waveguide. In Ref. [Reference Fuks and Schamiloglu6], the A6 magnetron has a diffraction output with six equally shaped cavities and converts the π mode to a ![]() $\textrm{TE}_{31}$ mode and the
$\textrm{TE}_{31}$ mode and the ![]() $2\pi/3$ mode to a
$2\pi/3$ mode to a ![]() $\textrm{TE}_{21}$ mode at high efficiency. However, since there is an interest in the HPM community to work with a
$\textrm{TE}_{21}$ mode at high efficiency. However, since there is an interest in the HPM community to work with a ![]() $\textrm{TE}_{11}$ mode, several attempts have been made to modify the diffraction output to convert the radiation directly into a
$\textrm{TE}_{11}$ mode, several attempts have been made to modify the diffraction output to convert the radiation directly into a ![]() $\textrm{TE}_{11}$ mode. In Ref. [Reference Li and Liu12], the diffraction output was modified to have two diametrically opposed large cavities and four small cavities, resulting in a
$\textrm{TE}_{11}$ mode. In Ref. [Reference Li and Liu12], the diffraction output was modified to have two diametrically opposed large cavities and four small cavities, resulting in a ![]() $\textrm{TE}_{11}$ mode when operating the magnetron in π mode. More recently, a diffraction output with four large and two small cavities was investigated using a semi-transparent cathode in Ref. [Reference Yang, Dong, Sun, Yang and Dong13], where the π mode was efficiently converted to a
$\textrm{TE}_{11}$ mode when operating the magnetron in π mode. More recently, a diffraction output with four large and two small cavities was investigated using a semi-transparent cathode in Ref. [Reference Yang, Dong, Sun, Yang and Dong13], where the π mode was efficiently converted to a ![]() $\textrm{TE}_{11}$ mode. This idea was also investigated independently in two master theses projects at the Swedish Defence Research Agency [Reference Thunberg14, Reference Sawert15], but by using cylindrical and transparent cathodes, respectively. Both studies concluded that conversion from the π mode to
$\textrm{TE}_{11}$ mode. This idea was also investigated independently in two master theses projects at the Swedish Defence Research Agency [Reference Thunberg14, Reference Sawert15], but by using cylindrical and transparent cathodes, respectively. Both studies concluded that conversion from the π mode to ![]() $\textrm{TE}_{11}$ mode was possible at high efficiency.
$\textrm{TE}_{11}$ mode was possible at high efficiency.

Figure 1. (a) 3D cross-section of the RM, showing the different regions and parts. (b) Diffraction output viewed from the cylindrical waveguide side, illustrating how the cavities extend from the interaction region.
The main objective of this paper is to further investigate the diffraction output with four large and two small cavities from [Reference Thunberg14, Reference Sawert15] using the transparent cathode from [Reference Fuks and Schamiloglu6], and to show efficient conversion to a ![]() $\textrm{TE}_{11}$ mode. Furthermore, we present a novel method for minimizing the leakage current from the interaction region that does not compromise the performance. The leakage current is caused by electrons leaving the interaction region in the axial direction, which can potentially reduce efficiency and cause damage to the inner structure of the RM or the vacuum window. A common approach to minimize the leakage current is to use endcaps at the ends of the interaction region [Reference Yang, Dong, Yang and Dong11, Reference Leach, Prasad, Fuks and Schamiloglu16]. For instance, in an experimental study of the A6 magnetron with transparent cathode, a spherical endcap was introduced [Reference Leach, Prasad, Fuks, Buchenauer, McConaha and Schamiloglu17]. However, physical damage was reported on the spherical endcap after experiments.
$\textrm{TE}_{11}$ mode. Furthermore, we present a novel method for minimizing the leakage current from the interaction region that does not compromise the performance. The leakage current is caused by electrons leaving the interaction region in the axial direction, which can potentially reduce efficiency and cause damage to the inner structure of the RM or the vacuum window. A common approach to minimize the leakage current is to use endcaps at the ends of the interaction region [Reference Yang, Dong, Yang and Dong11, Reference Leach, Prasad, Fuks and Schamiloglu16]. For instance, in an experimental study of the A6 magnetron with transparent cathode, a spherical endcap was introduced [Reference Leach, Prasad, Fuks, Buchenauer, McConaha and Schamiloglu17]. However, physical damage was reported on the spherical endcap after experiments.
In this study, we show that it is possible to reduce the leakage current by increasing the length of the interaction region without using endcaps. As such, we avoid potential issues related to endcaps. Also, by keeping the cathode flat we keep the manufacturing process simple and prevent locally high electric fields in areas with a small radius of curvature.
Another benefit of working with the ![]() $\textrm{TE}_{11}$ mode is that it makes it possible to reduce the radius of the cylindrical waveguide, since the cutoff frequency of the
$\textrm{TE}_{11}$ mode is that it makes it possible to reduce the radius of the cylindrical waveguide, since the cutoff frequency of the ![]() $\textrm{TE}_{11}$ mode is lower than the
$\textrm{TE}_{11}$ mode is lower than the ![]() $\textrm{TE}_{31}$ mode. Consequently, both the waveguide and the diffraction output become smaller, which benefits compactness. For the proposed RM (with a 7 cm radius where the π mode resonates near 2.5 GHz), the propagating modes are reduced to only the
$\textrm{TE}_{31}$ mode. Consequently, both the waveguide and the diffraction output become smaller, which benefits compactness. For the proposed RM (with a 7 cm radius where the π mode resonates near 2.5 GHz), the propagating modes are reduced to only the ![]() $\textrm{TE}_{11}$,
$\textrm{TE}_{11}$, ![]() $\textrm{TM}_{01}$, and
$\textrm{TM}_{01}$, and ![]() $\textrm{TE}_{21}$ modes.
$\textrm{TE}_{21}$ modes.
Lastly, we investigate the possibility of operating the RM at a lower voltage. Most RMs operate at voltages exceeding 400 kV, which is beneficial for obtaining high output power. However, high voltage increases the risk of electrical breakdown (e.g., RF breakdown outside the vacuum window) and reduces the lifetime of components, e.g., the emitter [Reference Baturin, Kelly, Mousa, Gribb, Martens and Sheshin18]. In particular, by lowering the voltage, the intention is to reduce the surface current density on the emitter to improve its lifetime and still demonstrate high efficiency with a reasonable amount of peak output power. Another benefit is that the RM can be operated using a smaller primary energy source (Marx generator). Furthermore, a lower voltage makes it possible to operate the RM using a simpler system for the Helmholtz pair (that generates the axial magnetic field), as the magnetic field strength can be reduced in the interaction region.
Model
Figure 1a depicts a cross-section of the RM. The coaxial input is followed by the interaction region, where the cathode splits into six separate stalks, hence defining the transparent cathode. This configuration enables electrons to have a trajectory that goes in between the cathode stalks, thus allowing for a longer time of travel before they eventually hit the cathode or the anode. The generated microwaves inside the interaction region are then fed through the diffraction output to the cylindrical waveguide. The six cavities in the interaction region are tapered through the diffraction output. However, as shown in Fig. 1b, only four cavities are tapered completely to the end of the waveguide, whereas the remaining two cavities are simply extruded from the interaction region.
A MAGIC3D [Reference Goplen, Ludeking, Smith and Warren19] model of the interaction region of the RM is shown in Fig. 2, where the different radii and angles are outlined. The transparent cathode orientation, denoted θ, was defined as the angle measured counter-clockwise from the midpoint of a cavity to the midpoint of the nearest cathode stalk. Furthermore, Fig. 3 displays the RM from the side, showing the lengths of the interaction region and the emitter, as well as the radius of the Helmholtz pair. An absorbing boundary condition was defined at the end of the output waveguide, depicted in purple. The values of the parameters used are shown in Table 1.

Figure 2. r-ϕ cross-section of the interaction region, illustrating the six cathode stalks and the six cavities in the anode. The lengths are shown in red while the angles are shown in blue.

Figure 3. r-z cross-section of the interaction region, shown between two cavities and with a cathode stalk present. The pair of Helmholtz coils are depicted in yellow outside the structure.
Table 1. Parameters of the RM. The last three parameters were varied

Method
The simulations in MAGIC3D were conducted by applying a voltage at the input, denoted Vin. This voltage was simulated using a ramp function with a rise time of 4 ns. However, due to the impedance of the system, the measured voltage over the A-K gap, Vac, will be lower than Vin. To generate the magnetic field, a pair of Helmholtz coils were positioned outside the structure in a symmetrical manner around the emitter with radius Rcoil, shown in Fig. 3. This ensures an almost uniform magnetic field inside the interaction region.
Studies were performed for three different geometrical parameters of the RM; the transparent cathode orientation θ, the emitter length Le, and the interaction region length Lint. By rotating the cathode, the electric field structure in the interaction region changes due to the symmetries of the transparent cathode and the anode structure. This can in turn affect the electron dynamics and trajectories, subsequently impacting the overall performance. Due to the symmetric structure, it is sufficient to study the angle θ for the values 0∘ to 60∘.
The study of the emitter length focused on values ranging from 4 to 8.5 cm. Emitter lengths shorter than 4 cm were considered impractical due to the system exhibiting a too-high impedance and current density. The main benefit of increasing the emitter size is that it can lower the local current density on the emitter, which can improve its lifetime.
As for the length of the interaction region, the objective is to study how it affects the leakage current and the magnetron performance. Note that in the interaction region, the magnetic field only has an axial component (see Fig. 3). Hence, electrons can move freely in the axial direction when they gain axial velocity from Coulomb collisions in the interaction region. Due to the strong electric field in the interaction region, most electrons will reach the anode within this area. However, a small fraction of the electrons will escape the interaction region. These electrons then enter the region where the magnetic field lines start to diverge. Consequently, the electrons will follow the field lines until they intersect a wall (or vacuum window). The objective here is to find out if the leakage current can be minimized by extending the interaction region. To achieve this, we investigate a range of lengths, varying from 11.5 to 23.5 cm.
For the parameter study of θ, four different combinations of voltages and magnetic fields were used. Input voltages Vin of 350 and 400 kV were applied for 0.28 T and 0.30 T. For the studies of the emitter length and interaction region length, the applied voltage and magnetic field were held constant at ![]() $V_{in} = 400$ kV and B = 0.30 T.
$V_{in} = 400$ kV and B = 0.30 T.
The net cathode current Ic was defined as the difference between the total emitted current and the return current that hit the cathode surface. Hence, the input power was calculated as ![]() $P_{in} = V_{ac} \cdot I_c$ while the output power Pout was measured at the end of the waveguide by integrating the axial component of the Poynting vector over the whole cross-section. Since the output power oscillates, its time-average
$P_{in} = V_{ac} \cdot I_c$ while the output power Pout was measured at the end of the waveguide by integrating the axial component of the Poynting vector over the whole cross-section. Since the output power oscillates, its time-average ![]() $\overline{P}_{out}$ was used to calculate the efficiency η, which was defined as
$\overline{P}_{out}$ was used to calculate the efficiency η, which was defined as ![]() $\eta = \overline{P}_{out}/P_{in}$.
$\eta = \overline{P}_{out}/P_{in}$.
For the optimized geometry, i.e., the geometry that resulted in the highest efficiency, a B-V study was performed, where the voltage over the A-K gap Vac was varied from 164 to 356 kV for a magnetic field strength B between 0.24 and 0.34 T.
Results
Parameter studies
The efficiencies with respect to the transparent cathode orientation are shown in Fig. 4. For all cases where the efficiency exceeds about 27%, a π mode was excited in the interaction region that converted to a ![]() $\textrm{TE}_{11}$ mode after passing the diffraction output. The black-dashed line is the only case not exhibiting a clear maximum in efficiency, as the variation with respect to the angle θ is small. The remaining cases all exhibit maxima near 10∘ to 20∘, however, the variation is still small and does not exceed about 5 percentage units.
$\textrm{TE}_{11}$ mode after passing the diffraction output. The black-dashed line is the only case not exhibiting a clear maximum in efficiency, as the variation with respect to the angle θ is small. The remaining cases all exhibit maxima near 10∘ to 20∘, however, the variation is still small and does not exceed about 5 percentage units.

Figure 4. Efficiency for different transparent cathode orientations θ for four combinations of Vin and B.
Note that a drastic decrease in efficiency occurs for ![]() $V_{in} = 400$ kV and B = 0.28 T at θ = 5∘, 50∘, and 55∘. At these angles, the
$V_{in} = 400$ kV and B = 0.28 T at θ = 5∘, 50∘, and 55∘. At these angles, the ![]() $2\pi/3$ mode (which has two electron spokes in the interaction region as shown in Fig. 15a) was excited instead of the π mode. The
$2\pi/3$ mode (which has two electron spokes in the interaction region as shown in Fig. 15a) was excited instead of the π mode. The ![]() $2\pi/3$ mode converts to a
$2\pi/3$ mode converts to a ![]() $\textrm{TE}_{21}$ mode after passing the diffraction output (see Fig. 15b). Since the diffraction output is not optimized for converting into a
$\textrm{TE}_{21}$ mode after passing the diffraction output (see Fig. 15b). Since the diffraction output is not optimized for converting into a ![]() $\textrm{TE}_{21}$ mode, the efficiency becomes low. The reason that a
$\textrm{TE}_{21}$ mode, the efficiency becomes low. The reason that a ![]() $2\pi/3$ mode is observed is due to the voltage over the A-K gap, which is approximately
$2\pi/3$ mode is observed is due to the voltage over the A-K gap, which is approximately ![]() $V_{ac} = 260$ kV for these cases. Hence, the voltage is just below the Buneman–Hartree voltage for the
$V_{ac} = 260$ kV for these cases. Hence, the voltage is just below the Buneman–Hartree voltage for the ![]() $2\pi/3$ mode, which for B = 0.28 T is
$2\pi/3$ mode, which for B = 0.28 T is ![]() $V_{BH, 2\pi/3} = 282$ kV. Despite being below
$V_{BH, 2\pi/3} = 282$ kV. Despite being below ![]() $V_{BH, 2\pi/3}$, it appears that the
$V_{BH, 2\pi/3}$, it appears that the ![]() $2\pi/3$ mode can be excited by chance.
$2\pi/3$ mode can be excited by chance.
In Fig. 5, the peak output power and efficiency are shown for different emitter lengths. The best performance is observed for emitter lengths between 4 and 5.5 cm, where the highest efficiency is ![]() $37\%$ with a corresponding peak power near 590 MW. Due to the loss in performance, there is no benefit in having an emitter longer than about 6.5 cm.
$37\%$ with a corresponding peak power near 590 MW. Due to the loss in performance, there is no benefit in having an emitter longer than about 6.5 cm.

Figure 5. Efficiency and peak output power for different emitter lengths with ![]() $V_{in} = 400$ kV and B = 0.30 T.
$V_{in} = 400$ kV and B = 0.30 T.
Figure 6 shows how the interaction region length Lint affects the peak power and efficiency. Within the interval 11.5–19.5 cm, we observe good performance in general, where the efficiency peaks at ![]() $37\%$ for
$37\%$ for ![]() $L_{int} = 13.5$ cm. The peak power within this range varies between 530 and 590 MW. For
$L_{int} = 13.5$ cm. The peak power within this range varies between 530 and 590 MW. For ![]() $L_{int} \gt 19.5$ cm, we observe a fast performance drop for both peak power and efficiency.
$L_{int} \gt 19.5$ cm, we observe a fast performance drop for both peak power and efficiency.

Figure 6. Efficiency and peak output power for different interaction region lengths with ![]() $V_{in} = 400$ kV and B = 0.30 T.
$V_{in} = 400$ kV and B = 0.30 T.
The leakage current and net cathode current are shown in Fig. 7. We note that the total net cathode current increases with Lint. Despite the increased current, the fraction of leakage current (red dashed curve) quickly drops with increasing length. For ![]() $L_{int} = 13.5$ cm, the leakage current is ∼10
$L_{int} = 13.5$ cm, the leakage current is ∼10![]() $\%$, while for
$\%$, while for ![]() $L_{int} = 19.5$ cm (where the performance is still good), the leakage current is less than
$L_{int} = 19.5$ cm (where the performance is still good), the leakage current is less than ![]() $1\%$.
$1\%$.

Figure 7. Net cathode current and leakage current as a ratio of net cathode current for different interaction region lengths with ![]() $V_{in} = 400$ kV and B = 0.30 T.
$V_{in} = 400$ kV and B = 0.30 T.
Figure 8 shows the input, output, and average output powers over time for the case with the highest efficiency and ![]() $\theta = 15^\circ$,
$\theta = 15^\circ$, ![]() $L_e = 4.5$ cm, and
$L_e = 4.5$ cm, and ![]() $L_{int} = 13.5$ cm. The reference values of
$L_{int} = 13.5$ cm. The reference values of ![]() $V_{in} = 400$ kV and B = 0.30 T were used for a total time of 50 ns. At steady-state, the voltage over the A-K gap, Vac, stabilizes at 261 kV (see Fig. 12). The input power stabilizes at 800 MW after ∼11 ns, while the peak output power reaches its maximum at 590 MW after ∼15 ns. Note that between 4 and 6 ns, the input power Pin drops with about 200 MW. Within this interval, the voltage Vac increases weakly (see Fig.12), hence the drop is explained by a fast-dropping net cathode current shown in Fig. 9. At about 7 ns, both the input power and net cathode current increase again. This occurs because the π mode starts to oscillate in the interaction region. The π mode for a six-cavity magnetron is characterized by having three electron spokes in the interaction region, as illustrated in Fig. 10a. Consequently, this resulted in a
$V_{in} = 400$ kV and B = 0.30 T were used for a total time of 50 ns. At steady-state, the voltage over the A-K gap, Vac, stabilizes at 261 kV (see Fig. 12). The input power stabilizes at 800 MW after ∼11 ns, while the peak output power reaches its maximum at 590 MW after ∼15 ns. Note that between 4 and 6 ns, the input power Pin drops with about 200 MW. Within this interval, the voltage Vac increases weakly (see Fig.12), hence the drop is explained by a fast-dropping net cathode current shown in Fig. 9. At about 7 ns, both the input power and net cathode current increase again. This occurs because the π mode starts to oscillate in the interaction region. The π mode for a six-cavity magnetron is characterized by having three electron spokes in the interaction region, as illustrated in Fig. 10a. Consequently, this resulted in a ![]() $\textrm{TE}_{11}$ mode at the waveguide, depicted in Fig. 10b. Regarding the frequency of the
$\textrm{TE}_{11}$ mode at the waveguide, depicted in Fig. 10b. Regarding the frequency of the ![]() $\textrm{TE}_{11}$ mode, the Fast Fourier Transform (FFT) of the output microwaves in Fig. 11 shows a distinct peak at f = 2.57 GHz.
$\textrm{TE}_{11}$ mode, the Fast Fourier Transform (FFT) of the output microwaves in Fig. 11 shows a distinct peak at f = 2.57 GHz.

Figure 8. Time evolution of the input, output, and average output powers for ![]() $V_{in} = 400$ kV and B = 0.30 T.
$V_{in} = 400$ kV and B = 0.30 T.

Figure 9. Time evolution of the net cathode current and the leakage current for ![]() $V_{in} = 400$ kV and B = 0.30 T.
$V_{in} = 400$ kV and B = 0.30 T.

Figure 10. Simulation with ![]() $V_{in} = 400$ kV and B = 0.3 T at time t = 20 ns. (a) r-ϕ cross-section of the interaction region, showing a π mode with three electron spokes. (b) r-ϕ cross-section of the waveguide, showing the radial electric field component Er, with higher values depicted in yellow and lower values depicted in blue. The pattern illustrates a
$V_{in} = 400$ kV and B = 0.3 T at time t = 20 ns. (a) r-ϕ cross-section of the interaction region, showing a π mode with three electron spokes. (b) r-ϕ cross-section of the waveguide, showing the radial electric field component Er, with higher values depicted in yellow and lower values depicted in blue. The pattern illustrates a ![]() $\textrm{TE}_{11}$ mode.
$\textrm{TE}_{11}$ mode.

Figure 11. FFT of the output microwaves for ![]() $V_{in} = 400$ kV and B = 0.30 T, showing one peak at f = 2.57 GHz. The FFT was captured over the whole time range of 0–50 ns.
$V_{in} = 400$ kV and B = 0.30 T, showing one peak at f = 2.57 GHz. The FFT was captured over the whole time range of 0–50 ns.

Figure 12. Time evolution of the voltages over the A-K gap for three cases with different magnetic field strengths. Note that the voltages in this graph have been filtered from noise.
Figure 9 also shows the leakage current over time. The results show that the leakage current is significant up to about when the π mode starts to resonate, and then drops, indicating that more electrons stay within the interaction region during π mode operation.
B-V study
For the optimized geometry (![]() $\theta = 15^\circ$,
$\theta = 15^\circ$, ![]() $L_{e} = 4.5$ cm,
$L_{e} = 4.5$ cm, ![]() $L_{int} = 13.5$ cm), different voltages and magnetic fields were applied. Figure 12 shows the time evolution of Vac for this geometry for three different values of B and Vin. All the voltages reach their maxima after ∼5–6 ns, and then drop to stabilize at slightly lower steady-state values. The voltage drops either because it enters a mode competition stage or the π mode starts to resonate. Mode competition is characterized by several cavity modes being excited in the interaction region with no significant microwave power generation. For the case with B = 0.26 T and
$L_{int} = 13.5$ cm), different voltages and magnetic fields were applied. Figure 12 shows the time evolution of Vac for this geometry for three different values of B and Vin. All the voltages reach their maxima after ∼5–6 ns, and then drop to stabilize at slightly lower steady-state values. The voltage drops either because it enters a mode competition stage or the π mode starts to resonate. Mode competition is characterized by several cavity modes being excited in the interaction region with no significant microwave power generation. For the case with B = 0.26 T and ![]() $V_{in} = 300$ kV, mode competition occurs between 5 and 16 ns and then the voltage drops to stabilize at 210 kV when a π mode starts to resonate. For the other two cases, the π mode starts to resonate near 7 ns, hence the voltage stabilizes earlier with no mode competition occurring.
$V_{in} = 300$ kV, mode competition occurs between 5 and 16 ns and then the voltage drops to stabilize at 210 kV when a π mode starts to resonate. For the other two cases, the π mode starts to resonate near 7 ns, hence the voltage stabilizes earlier with no mode competition occurring.
The efficiencies and peak output powers for the three cases are illustrated for a range of steady-state voltages Vac in Figs. 13 and 14, respectively. Note that for each case, there is a lower and an upper limit of Vac for which the π mode is excited. When operating outside these limits, a ![]() $\textrm{TE}_{21}$ mode is instead excited to the waveguide (see Fig. 15b). The Buneman–Hartree voltage VBH plays a crucial role in determining the excitation of modes in the interaction region. Specifically, it provides the minimum voltage required to excite a specific mode for a given magnetic field B. The relationship between B and VBH is written as [Reference Benford, Swegle and Schamiloglu2]:
$\textrm{TE}_{21}$ mode is instead excited to the waveguide (see Fig. 15b). The Buneman–Hartree voltage VBH plays a crucial role in determining the excitation of modes in the interaction region. Specifically, it provides the minimum voltage required to excite a specific mode for a given magnetic field B. The relationship between B and VBH is written as [Reference Benford, Swegle and Schamiloglu2]:
 \begin{equation}
\begin{aligned}
B = \frac{|V_{BH}|p}{d_e\omega r_a} + \frac{m_ec^2p}{ed_e\omega r_a} \left(1 - \sqrt{1 - \frac{(\omega r_a)^2}{(pc)^2}} \right),
\end{aligned}
\end{equation}
\begin{equation}
\begin{aligned}
B = \frac{|V_{BH}|p}{d_e\omega r_a} + \frac{m_ec^2p}{ed_e\omega r_a} \left(1 - \sqrt{1 - \frac{(\omega r_a)^2}{(pc)^2}} \right),
\end{aligned}
\end{equation}
Figure 13. Efficiency for different steady-state voltages over the A-K gap for three different magnetic fields.

Figure 14. Peak output power for different steady-state voltages over the A-K gap for three different magnetic fields.

Figure 15. Simulation with ![]() $V_{ac} = 247$ kV and B = 0.26 T at time t = 47 ns. (a) r-ϕ cross-section of the interaction region, showing a
$V_{ac} = 247$ kV and B = 0.26 T at time t = 47 ns. (a) r-ϕ cross-section of the interaction region, showing a ![]() $2\pi/3$ mode with two electron spokes. (b) r-ϕ cross-section of the waveguide, showing the radial electric field component Er, with higher values depicted in yellow and lower values depicted in blue. The pattern illustrates a
$2\pi/3$ mode with two electron spokes. (b) r-ϕ cross-section of the waveguide, showing the radial electric field component Er, with higher values depicted in yellow and lower values depicted in blue. The pattern illustrates a ![]() $\textrm{TE}_{21}$ mode.
$\textrm{TE}_{21}$ mode.
where p is the azimuthal mode number, ω the angular frequency, e the electron charge, me the electron mass, c the speed of light in vacuum, and ![]() $d_e = 2(r_a^2 - r_c^2)/r_a$.
$d_e = 2(r_a^2 - r_c^2)/r_a$.
For B = 0.26 T, B = 0.30 T, and B = 0.34 T, the Buneman–Hartree voltage for the π mode, ![]() $V_{BH, \pi}$, is 203, 241, and 278 kV, respectively. Note that
$V_{BH, \pi}$, is 203, 241, and 278 kV, respectively. Note that ![]() $V_{BH, \pi}$ was calculated using a frequency of 2.57 GHz. These theoretical predictions agree reasonably well with the results obtained in Fig. 13.
$V_{BH, \pi}$ was calculated using a frequency of 2.57 GHz. These theoretical predictions agree reasonably well with the results obtained in Fig. 13.
For excitation of the π mode, the case with B = 0.26 T shows the lowest efficiency, peaking at 31% with a peak output power of 263 MW. For the other two cases, efficiency peaks near 37% for B = 0.30 T and B = 0.34 T (but for different Vac), having peak output powers of 594 and 960 MW, respectively. Nevertheless, a noteworthy exception occurred for B = 0.30 T and ![]() $V_{ac} = 282$ kV, where a spontaneous excitation of the
$V_{ac} = 282$ kV, where a spontaneous excitation of the ![]() $2\pi/3$ mode took place, leading to a decrease in efficiency.
$2\pi/3$ mode took place, leading to a decrease in efficiency.
The peak output powers in Fig. 14 exhibit a continuous rise with increasing Vac and B, reaching maximum values of 400, 790 MW, and 1.1 GW, respectively. Similar to the efficiency, the spontaneous excitation of the ![]() $2\pi/3$ mode for B = 0.30 T and
$2\pi/3$ mode for B = 0.30 T and ![]() $V_{ac} = 282$ kV also decreases the peak output power substantially.
$V_{ac} = 282$ kV also decreases the peak output power substantially.
Furthermore, a broader range of values for Vac and B were simulated and plotted in a Hull–Buneman–Hartree (HBH) diagram, shown in Fig. 16. This diagram gives valuable information into the excitation of modes and their respective efficiencies. The minimum value of the magnetic field Bmin given a voltage Vac for which mode excitation is possible is determined by the Hull cutoff condition [Reference Benford, Swegle and Schamiloglu2]. As shown, the limit for the Hull cutoff condition is beyond the operational regime for π mode excitation. Instead, excitation of the π mode occurs when its Buneman–Hartree condition is fulfilled, i.e., for ![]() $V_{ac} \geq V_{BH, \pi}$. This excitation continues until Vac gets close to the Buneman–Hartree voltage of the
$V_{ac} \geq V_{BH, \pi}$. This excitation continues until Vac gets close to the Buneman–Hartree voltage of the ![]() $2\pi/3$ mode, i.e.,
$2\pi/3$ mode, i.e., ![]() $V_{BH, 2\pi/3}$, at which point the
$V_{BH, 2\pi/3}$, at which point the ![]() $2\pi/3$ mode becomes excited instead. As a result, an interval for π mode excitation is established:
$2\pi/3$ mode becomes excited instead. As a result, an interval for π mode excitation is established: ![]() $V_{BH, \pi} \leq V_{ac} \leq V_{BH, 2\pi/3}$. However, despite that only a π mode is expected within this interval, we still observe spontaneous
$V_{BH, \pi} \leq V_{ac} \leq V_{BH, 2\pi/3}$. However, despite that only a π mode is expected within this interval, we still observe spontaneous ![]() $2\pi/3$ mode excitation when operating just below
$2\pi/3$ mode excitation when operating just below ![]() $V_{BH, 2\pi/3}$ (shown in Fig. 16 by the diamond-shaped points with low efficiency). When operating above
$V_{BH, 2\pi/3}$ (shown in Fig. 16 by the diamond-shaped points with low efficiency). When operating above ![]() $V_{BH, 2\pi/3}$, only the
$V_{BH, 2\pi/3}$, only the ![]() $2\pi/3$ mode is excited.
$2\pi/3$ mode is excited.

Figure 16. Hull–Buneman–Hartree (HBH) diagram showing the Hull cutoff condition (black line), as well as the Buneman–Hartree condition for the ![]() $2\pi/3$ and π modes with the efficiency shown as a colorbar. Circles represent π mode excitation and diamonds
$2\pi/3$ and π modes with the efficiency shown as a colorbar. Circles represent π mode excitation and diamonds ![]() $2\pi/3$ mode excitation. Triangles represent cavity modes with four electron spokes, while crosses represent cases with no mode excitation.
$2\pi/3$ mode excitation. Triangles represent cavity modes with four electron spokes, while crosses represent cases with no mode excitation. ![]() $V_{BH, \pi}$ was calculated using a frequency of 2.57 GHz and
$V_{BH, \pi}$ was calculated using a frequency of 2.57 GHz and ![]() $V_{BH, 2\pi/3}$ with 2.35 GHz.
$V_{BH, 2\pi/3}$ with 2.35 GHz.
When operating below the Buneman–Hartree voltage ![]() $V_{BH, \pi}$, no π mode excitation is observed, which is in agreement with the Buneman–Hartree condition. Instead, we observe excitation of a cavity mode where the electron cloud has four spokes (marked as triangles in Fig. 16). This cavity mode converts to a propagating
$V_{BH, \pi}$, no π mode excitation is observed, which is in agreement with the Buneman–Hartree condition. Instead, we observe excitation of a cavity mode where the electron cloud has four spokes (marked as triangles in Fig. 16). This cavity mode converts to a propagating ![]() $\textrm{TE}_{21}$ mode in the cylindrical waveguide, but at low efficiency. The cavity mode is also observed in two cases above the voltage
$\textrm{TE}_{21}$ mode in the cylindrical waveguide, but at low efficiency. The cavity mode is also observed in two cases above the voltage ![]() $V_{BH, \pi}$, but does not generate significant microwave power (as indicated by the use of dark blue triangles). When this mode generates microwaves, its voltage should in theory drop to somewhere below
$V_{BH, \pi}$, but does not generate significant microwave power (as indicated by the use of dark blue triangles). When this mode generates microwaves, its voltage should in theory drop to somewhere below ![]() $V_{BH, \pi}$. However, the electron spokes for these particular cases never reach the anode inside the interaction region, instead, all the current is leaking in the axial direction. Consequently, when the voltage Vac reaches its peak, it remains elevated and results in a higher positioning in the HBH diagram. For even lower voltages, no cavity mode was excited as shown by the data points marked as crosses.
$V_{BH, \pi}$. However, the electron spokes for these particular cases never reach the anode inside the interaction region, instead, all the current is leaking in the axial direction. Consequently, when the voltage Vac reaches its peak, it remains elevated and results in a higher positioning in the HBH diagram. For even lower voltages, no cavity mode was excited as shown by the data points marked as crosses.
Discussion and conclusions
In this paper, a RM with a transparent cathode and a novel diffraction output was investigated. Parameter studies of the transparent cathode orientation, emitter length, and interaction region length were performed as well as a comprehensive study of how Vac and B affected the performance. From the parameter studies, we concluded that the new diffraction output can efficiently convert π mode excitation in the interaction region into a single ![]() $\textrm{TE}_{11}$ mode at the cylindrical waveguide. Furthermore, we found that there are favorable geometrical values for which the efficiency is maximized near 37%, having a
$\textrm{TE}_{11}$ mode at the cylindrical waveguide. Furthermore, we found that there are favorable geometrical values for which the efficiency is maximized near 37%, having a ![]() $\textrm{TE}_{11}$ mode. The peak efficiency was observed in several simulations with varying voltages and magnetic fields, but we particularly emphasized two cases. The first case had B = 0.30 T and
$\textrm{TE}_{11}$ mode. The peak efficiency was observed in several simulations with varying voltages and magnetic fields, but we particularly emphasized two cases. The first case had B = 0.30 T and ![]() $V_{ac} = 261$ kV, while the second had B = 0.34 T and
$V_{ac} = 261$ kV, while the second had B = 0.34 T and ![]() $V_{ac} = 318$ kV. The peak output powers were 590 and 960 MW, respectively. Additionally, we show that it is possible to use a smaller waveguide and operate at a lower voltage while maintaining good performance. The smaller waveguide is beneficial for compactness and for reducing the number of propagating modes to only three at the operating frequency of 2.57 GHz. By operating at lower voltage, the requirements for the primary energy source can be relaxed, while also allowing operation at lower magnetic field strength.
$V_{ac} = 318$ kV. The peak output powers were 590 and 960 MW, respectively. Additionally, we show that it is possible to use a smaller waveguide and operate at a lower voltage while maintaining good performance. The smaller waveguide is beneficial for compactness and for reducing the number of propagating modes to only three at the operating frequency of 2.57 GHz. By operating at lower voltage, the requirements for the primary energy source can be relaxed, while also allowing operation at lower magnetic field strength.
Furthermore, we show that it is possible to significantly reduce the electron leakage current by extending the interaction region without impacting efficiency too much (see Fig. 7). Consequently, we can avoid using endcaps that introduce additional geometrical features that increase the risk of high electric fields where the radius of curvature is small.
In this work, the HBH diagram in Fig. 16 was generated to understand the performance of the RM for different values of Vac and B. The π mode is excited when the voltage is above the Buneman–Hartree voltage for the π mode but below the Buneman–Hartree voltage for the ![]() $2\pi/3$ mode, i.e.,
$2\pi/3$ mode, i.e., ![]() $V_{BH,\pi} \leq V_{ac} \leq V_{BH,2\pi/3}$. The efficiency as a function of Vac for various B seems consistent, and the maximum is typically found a bit above
$V_{BH,\pi} \leq V_{ac} \leq V_{BH,2\pi/3}$. The efficiency as a function of Vac for various B seems consistent, and the maximum is typically found a bit above ![]() $V_{BH,\pi}$. The peak output power exhibited a steady rise as Vac increased above
$V_{BH,\pi}$. The peak output power exhibited a steady rise as Vac increased above ![]() $V_{BH,\pi}$ (see Fig. 14), presenting the possibility of achieving higher peak output power at the cost of lower efficiency.
$V_{BH,\pi}$ (see Fig. 14), presenting the possibility of achieving higher peak output power at the cost of lower efficiency.
For the proposed RM, the performance is highly dependent on which cavity mode is excited. Excitation of the π mode in the interaction region led to a favorable ![]() $\textrm{TE}_{11}$ mode with high efficiency and output power, whereas excitation of the
$\textrm{TE}_{11}$ mode with high efficiency and output power, whereas excitation of the ![]() $2\pi/3$ mode resulted in a
$2\pi/3$ mode resulted in a ![]() $\textrm{TE}_{21}$ mode with lower efficiency. For the latter case, the low efficiency occurs because the diffraction output performs poorly when converting the
$\textrm{TE}_{21}$ mode with lower efficiency. For the latter case, the low efficiency occurs because the diffraction output performs poorly when converting the ![]() $2\pi/3$ mode to a
$2\pi/3$ mode to a ![]() $\textrm{TE}_{21}$ mode. We note that in this study, excitation of the 2π mode was never observed.
$\textrm{TE}_{21}$ mode. We note that in this study, excitation of the 2π mode was never observed.
Note that it was found that the ![]() $2\pi/3$ mode is sometimes excited when operating the RM just below
$2\pi/3$ mode is sometimes excited when operating the RM just below ![]() $V_{BH,2\pi/3}$, i.e., where only a π mode is expected. While this is not fully understood, one possible explanation is that the Buneman–Hartree condition is not accurate for the
$V_{BH,2\pi/3}$, i.e., where only a π mode is expected. While this is not fully understood, one possible explanation is that the Buneman–Hartree condition is not accurate for the ![]() $2\pi/3$ mode when using a transparent cathode. This might be because the Buneman–Hartree condition is derived assuming a cylindrical cathode, therefore, it does not take into account additional effects caused by the transparent cathode stalks. However, when
$2\pi/3$ mode when using a transparent cathode. This might be because the Buneman–Hartree condition is derived assuming a cylindrical cathode, therefore, it does not take into account additional effects caused by the transparent cathode stalks. However, when ![]() $V_{ac} \gt V_{BH,2\pi/3}$, only a
$V_{ac} \gt V_{BH,2\pi/3}$, only a ![]() $2\pi/3$ mode was excited, but at low efficiency.
$2\pi/3$ mode was excited, but at low efficiency.
When operating the RM below ![]() $V_{BH,\pi}$, no π mode was observed, which is in agreement with the Buneman–Hartree condition. Instead, a different cavity mode was excited, where the electron cloud had four spokes (in Fig. 16, these cases are represented with triangles). This resulted in a
$V_{BH,\pi}$, no π mode was observed, which is in agreement with the Buneman–Hartree condition. Instead, a different cavity mode was excited, where the electron cloud had four spokes (in Fig. 16, these cases are represented with triangles). This resulted in a ![]() $\textrm{TE}_{21}$ mode at the cylindrical waveguide, but at low efficiency.
$\textrm{TE}_{21}$ mode at the cylindrical waveguide, but at low efficiency.
Acknowledgements
We thank Alan Aliyali at the Swedish Defence Research Agency and Dragos Dancila at Uppsala University for their contributions to this work. This research was funded by the Swedish Armed Forces.
Competing interests
None declared.

David Sawert received the M.Sc. degree in engineering physics from Uppsala University in 2023. He did his master’s thesis at the Swedish Defence Research Agency in the field of HPM and is currently working with electronic design at Saab Technologies in Stockholm.

Pablo Vallejos received his M.Sc. degree in engineering physics in 2009 from Uppsala University, Sweden. He then worked for COMSOL for 4 years with technical support and sales. In 2014, he began his doctorate in the field of plasma physics and nuclear fusion at the Royal Institute of Technology, Sweden, and received his Ph.D. degree in 2020. He is currently working with HPM research and technologies at the Swedish Defence Research Agency.

Frans Nyberg received the B.S. and M.S. degrees in engineering physics from the Royal Institute of Technology, Stockholm, Sweden, in 2020 and 2022, respectively. He is currently working at the Swedish Defence Research Agency in the microwave engineering field.

Tomas Hurtig received the M.Sc. degree in electrical engineering and the Ph.D. degree in plasma physics from the Royal Institute of Technology, Stockholm, in 1997 and 2004, respectively. Since 2004, he has been with FOI – Swedish Defence Research Agency at the Division of Weapons, Protection and Security. He is currently managing projects concerning Directed Energy Weapons and Plasma Assisted Combustion.