1. Introduction
Since the early 1990s, the beef cattle industry has become increasingly focused on carcass “end-point” marketing strategies (EPMSs) in an attempt to provide higher-quality and more consistent meat products for consumers (McKenna et al., Reference McKenna, Roberts, Bates, Schmidt, Hale, Griffin, Savell, Brooks, Morgan, Montgomery, Belk and Smith2002). Platter et al. (Reference Platter, Tatum, Belk, Koontz, Chapman and Smith2005), and many others,Footnote 1 have routinely demonstrated that consumers are willing to pay higher premiums for beef that has a higher-quality grade. In an effort to meet this demand, feedlot operators attempt to market their cattle at U.S. Department of Agriculture (USDA) Choice quality grade based on visual assessments of back fat (0.4 to 0.5 inches of back fat). The result of this focus is evident as a growing percentage of carcasses grade Choice each year. Although this strategy may ultimately address consumer needs, EPMS does not necessarily result in profit maximization unless cattle feeders are adequately compensated for the added costs over time for attaining the demanded target. Additionally, though cattle feeders routinely maintain individual identification for their herd health and accounting systems, they rarely market cattle based on individual characteristics. Because cattle are not marketed on an individual basis, it has been estimated that 25% of cattle are “underfed” and 25% are “overfed” (Brethour, Reference Brethour2000).
A classic profit maximization decision rule described in production economic text books is to choose the amount of input(s) where the value of the marginal product equals the marginal factor cost of production (e.g., Beattie et al., Reference Beattie, Taylor and Watts1985). Beef cattle feeders experience two major production decisions in relation to a specific pen of cattle. The first decision is the choice of production process including types of inputs. The second, and final, decision is when the animal(s) should be sold given market conditions and production efficiency. However, in regard to a biological process, time and genetic variation are dimensions that complicate this decision rule and are often ignored in general expositions of profit maximization for livestock producers. In livestock production, inputs from the first decision are added at multiple points over time (typically daily), but revenues are realized only once. Therefore, the optimal quantity of inputs is directly related to the amount of time that the animal is exposed to the production process. As a result, the primary objective of this research is to determine a method for assessing cattle growth and using this information to test the outcomes of a profit maximizing end-point rule versus the traditional carcass end-point rule for fed beef cattle.
The realization of maximum profitability requires livestock producers to account for continuous and dynamic growth (i.e., weight and carcass characteristics) and its impacts on both cost and revenue. As far as the researchers are aware, no academic research has considered integrating dynamic nonlinear growth functions into the profit objective function, and thus, this constitutes our major contribution to the literature. This is surprising as there are numerous nonlinear growth functions that are routinely estimated in the biological and scientific literature for numerous species of animals including cattle, pork, lambs, and poultry.
The major finding of this article is that a simple profit maximization rule (PMR) leads to higher average profits per head than the cattle industry's EPMS (targeting a specific weight and/or 0.4 to 0.5 inches of back fat). Our results from analyzing 1,467 head of individually marketed cattle through the Mississippi Farm to Feedlot Program indicated that the average opportunity cost of EPMS ranged from $6.71 to $8.71 per head, depending on the price received. Greater estimates are found using alternative growth models.
2. Literature
We first discuss the relevant literature pertaining to the general use of dynamic growth functions. Next, a brief background of the relevant literature pertaining to the beef cattle feeding industry is summarized.
2.1. Growth Functions
The use of dynamic nonlinear growth functions to predict the growth of living species is a well-established practice in the biological and scientific literature as there are many applications for these types of growth functions in the animal and plant science arenas. Recently, Strathe et al. (Reference Strathe, Danfær, Sørensen and Kebreab2010) utilized nonlinear growth functions to model pig growth, whereas Khamis et al. (Reference Khamis, Ismail, Haron and Muhammad2005) used these functions to estimate palm oil yields.
Specific to the cattle industry, research that estimates dynamic nonlinear growth functions is well established. Brown et al. (Reference Brown, Fitzhugh and Cartwright1976) compared the effectiveness of five different growth functions when modeling weight-age relationships for female cattle. They estimated the Logistic, Gompertz, Richards, and Brody growth functions and found the Brody function to be the best predictor of weight for their application. Goonewardene et al. (Reference Goonewardene, Berg and Hardin1981) developed a similar approach using the Logistic, Richards, Brody, and Von Bertalanffy functions to analyze the growth of female cattle. Forni et al. (Reference Forni, Piles, Blasco, Varona, Oliveira, Lôbo and Albuquerque2009) provided another example in which these growth functions are used to model the growth of Nelore female cattle. Each of these studies analyzed the growth of cattle over multiple years (life cycle) of data as these females are tracked from birth through the removal from the breeding herd.
There are several dynamic nonlinear growth functions to consider when estimating biological growth (Tsoularis and Wallace, Reference Tsoularis and Wallace2002). Estimates of growth in animals are obtained by tracking live animal weight over time (age), and the functional form is often chosen by how well it fits the data and its computational ease (Brown et al., Reference Brown, Fitzhugh and Cartwright1976; Lopez et al., Reference Lopez, France, Gerrits, Dhanoa, Humphries and Dijkstral2000). Growth functions can be estimated for either an individual or groups of animals by estimating nonlinear biological parameters, such as the intrinsic rate of growth over time (e.g., Brown et al., Reference Brown, Fitzhugh and Cartwright1976; Menchaca et al., Reference Menchaca, Chase, Olson and Hammond1996; Perotto et al., Reference Perotto, Coe and Lee1992). Furthermore, it has been shown that growth and nutrient requirements are interrelated, and feed sources necessarily impact growth rates (Pereda-Solis et al., Reference Pereda-Solis, Gonzalez-Munoz, Arjona-Suarez, Bueno-Auilar, Mendoza Martinez, Ramirez and Martinez Guerrero2011; Perry and Fox, Reference Perry and Fox1997).
2.2. Fed Cattle Industry
Much research has focused on the determinants of profitability and the adoption of new technology to predict carcass characteristics, and hence value. Langemeier et al. (Reference Langemeier, Schroeder and Mintert1992), Lawrence et al. (Reference Lawrence, Wang and Loy1999), and Mark et al. (Reference Mark, Schroeder and Jones2000), among others, identified factors that influence cattle feeding profitability, focusing primarily on input and output prices. Cattle slaughter weight is often noted in the literature as significantly impacting profitability, regardless of the marketing method. For instance, Feuz (Reference Feuz, Ward, Feuz and Schroeder1999) found that body weight explains 96% to 100% of the variation in revenue when cattle are sold on the cash market. Furthermore, Johnson and Ward (Reference Johnson and Ward2005) found that carcass (and hence live body) weight explains 61% to 71% of the variation in revenue when cattle are sold under carcass merit (formula) pricing. Johnson and Ward (Reference Johnson and Ward2006) found in their study of formula pricing, that carcass weight sends a stronger signal to producers than (noisy) carcass quality characteristics.
Other research has focused on the profitability differences between different pricing methods including formula (based on the value of various individual animal carcass characteristics), carcass weight, and live weight pricing (Feuz et al., Reference Feuz, Fausti and Wagner1993; Johnson and Ward, Reference Johnson and Ward2005, Reference Johnson and Ward2006; McDonald and Schroeder, Reference McDonald and Schroeder2003). Although each strategy can be optimal based on market conditions and animal profiles, profit variability is least for live weight pricing and greatest for formula pricing (Koontz et al., Reference Koontz, Hoag, Brethour and Walker2008). As such, formula pricing shifts the risk of the animal's true value from the processor to the feeder. Additionally, analyses of using ultrasound and genetic testing technologies to improve carcass estimates of a live animal have been conducted (DeVuyst et al., Reference DeVuyst, Bullinger, Bauer, Berg and Larson2007; Lusk et al., Reference Lusk, Little, Williams, Anderson and McKinley2003). Such research follows the rationale that additional information improves pricing method choice and returns to the seller. For instance, Schroeder and Graff (Reference Schroeder and Graff2000) found that average revenues could be improved from $15 to $35 per head if producers had perfect foresight as to animals’ quality and yield grade prior to slaughter. Similar analyses have been conducted by DeVuyst et al. (Reference DeVuyst, Bullinger, Bauer, Berg and Larson2007) using animal genotyping and by Walburger and Crews (Reference Walburger and Crews2004) using animal parentage.
Lusk et al. (Reference Lusk, Little, Williams, Anderson and McKinley2003) used ultrasound technology to predict carcass qualities and estimated the value of the information over the three main marketing methods: live weight, carcass weight, and formula pricing. They analyzed data from 163 animals from Mississippi State University's Mississippi Farm to Feedlot Program. They found that using ultrasound information could have increased revenue by approximately $25 or $33 per head for cattle marketed on a live or grid basis, respectively.
Previous studies have also shown increases in profitability based on a variety of different market timing approaches (Koontz et al., Reference Koontz, Hoag, Walker and Brethour2000, Reference Koontz, Hoag, Brethour and Walker2008; Lusk et al., Reference Lusk, Little, Williams, Anderson and McKinley2003). Koontz et al. (Reference Koontz, Hoag, Brethour and Walker2008) estimated the value of sorting cattle utilizing ultrasound technology in combination with three animal growth and carcass development curves to predict slaughter weight, USDA quality grade, and USDA yield grade. To predict carcass weight at any point in time, they utilized a linear standard growth curve and assumed cattle gain 3.2 pounds per day. Koontz et al. (Reference Koontz, Hoag, Brethour and Walker2008) found a $15 to $25 per head increase in returns from sorting cattle multiple times in the final 80 days prior to slaughter, and they estimated the marginal increase in fixed cost from sorting to be $5.70 per head. They also reported that the opportunity cost of overfeeding cattle is much greater than underfeeding due to the additional feed cost.
3. Theoretical Profit Maximization Model
Assuming the production technology has been chosen in advance,Footnote 2 we represent the competitive producer's dynamic profit response function as
In equation (1), the ith animal's output price, pi
(M(t), H
i
(t)) ∈ P, is derived from a vector of market variables, M(t), and a vector of hedonic value adjustments, H
i
(t) (e.g., perceived carcass quality, age, and weight within a preferred range). Whereas it is largely accepted that fed cattle prices generally follow seasonal patterns (Anderson and Trapp, Reference Anderson and Trapp2000), we assume that market variables are independent of the producer's short-run market timing decision and take the buyer's hedonic value adjustments as given. The animal's weight,
![]() $y_i (t|{\Omega }_i ) \in Y$
, at any moment during the production process is a function of time, conditional on a vector of exogenous, intrinsic, and heterogeneous biological parameters,
$y_i (t|{\Omega }_i ) \in Y$
, at any moment during the production process is a function of time, conditional on a vector of exogenous, intrinsic, and heterogeneous biological parameters,
![]() ${\Omega }_i$
(e.g., the animal's genetic makeup and weather). The type and relative impact of these parameters determines the functional form of the underlying nonlinear growth equation of motion,
${\Omega }_i$
(e.g., the animal's genetic makeup and weather). The type and relative impact of these parameters determines the functional form of the underlying nonlinear growth equation of motion,
![]() $\frac{{\partial y_i (t|{\Omega }_i )}}{{\partial t}}$
. Production costs are a vector of time-dependent input prices and quantities provided denoted as ci
(w(t)
T
x
i
(t)) ∈ C—that is, price of feed (wc
) and feed consumption (xc
i
), daily yardage charges (wy
), and random medicine charges (wv
) and usage (xv
i
)—and Fi
is the summation of all other time-independent fixed and sunk costs applicable to all animals (i.e., transportation, input price of cattle, and processing costs).
$\frac{{\partial y_i (t|{\Omega }_i )}}{{\partial t}}$
. Production costs are a vector of time-dependent input prices and quantities provided denoted as ci
(w(t)
T
x
i
(t)) ∈ C—that is, price of feed (wc
) and feed consumption (xc
i
), daily yardage charges (wy
), and random medicine charges (wv
) and usage (xv
i
)—and Fi
is the summation of all other time-independent fixed and sunk costs applicable to all animals (i.e., transportation, input price of cattle, and processing costs).
Not explicitly represented in the model is the relationship between growth and feed consumption (Pereda-Solis et al., Reference Pereda-Solis, Gonzalez-Munoz, Arjona-Suarez, Bueno-Auilar, Mendoza Martinez, Ramirez and Martinez Guerrero2011; Perry and Fox, Reference Perry and Fox1997). Maintenance requirements of beef cattle are driven primarily by body weight; as an animal grows, it requires more total energy to meet those demands. Nonetheless, there are biological constraints to how much feedstuffs cattle can consume, impacted by factors such as fiber content and type (Defoor et al., Reference Defoor, Galyean, Salyer, Nunnery and Parsons2002), as well as grain processing (Zinn et al., Reference Zinn, Owens and Ware2002). Furthermore, cattle are free to choose their feed consumption (unless limit fed), and their inherent efficiency of converting any form of inputs to growth is necessarily heterogeneous. These two natural conditions are often difficult to incorporate. For example, cattle feeding closeout data are often generalized to represent feed provided throughout the feeding process and do not include individual, daily consumption. This is the case with data used for this study, and therefore, we must assume fixed technologies with respect to feed inputs. Therefore, these have been ignored in past dynamic fed cattle models intended to solve for optimal weight and replacement policy (Hertzler, Reference Hertzler1988; Trapp, Reference Trapp1989), and this rationale will be followed within this study. In all, given that we assume the feeder's production technology is exogenous and constant, the control variable for the feeder is the time (days on feed) the animal is exposed to the production technology.
Generally, for a unique optimal market timing to exist, the time chosen must satisfy both the necessary condition,
 \begin{equation}
\frac{{d\pi _i }}{{dt}} = \underbrace {p_i ^{\prime} ({\bf M}(t),{\bf H}_i (t)) \cdot y_i (t|{\Omega }_i ) + p_i ({\bf M}(t),{\bf H}_i (t)) \cdot y_i ^{\prime} (t|{\Omega }_i )}_{{\rm value\ of\ the\ marginal\ product}} - \underbrace {c_i ^{\prime} ({\bf w}(t)^T {\bf x}_i (t))}_{{\rm marginal\ factor\ cost}} = 0,\end{equation}
\begin{equation}
\frac{{d\pi _i }}{{dt}} = \underbrace {p_i ^{\prime} ({\bf M}(t),{\bf H}_i (t)) \cdot y_i (t|{\Omega }_i ) + p_i ({\bf M}(t),{\bf H}_i (t)) \cdot y_i ^{\prime} (t|{\Omega }_i )}_{{\rm value\ of\ the\ marginal\ product}} - \underbrace {c_i ^{\prime} ({\bf w}(t)^T {\bf x}_i (t))}_{{\rm marginal\ factor\ cost}} = 0,\end{equation}
and the sufficient condition,
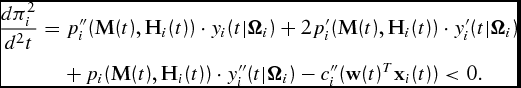 \begin{eqnarray}
\frac{{d\pi _i^2 }}{{d^2 t}} &=& p_i ^{\prime\prime} ({\bf M}(t),{\bf H}_i (t)) \cdot y_i (t|{\Omega }_i ) + 2p_i ^{\prime} ({\bf M}
(t),{\bf H}_i (t)) \cdot y_i ^{\prime} (t|{\Omega }_i )\nonumber\\
&& +\, p_i ({\bf M}(t),{\bf H}_i (t)) \cdot y_i ^{\prime\prime} (t|{\Omega }_i ) - c_i ^{\prime\prime}
({\bf w}(t)^T {\bf x}_i (t)) < 0.
\end{eqnarray}
\begin{eqnarray}
\frac{{d\pi _i^2 }}{{d^2 t}} &=& p_i ^{\prime\prime} ({\bf M}(t),{\bf H}_i (t)) \cdot y_i (t|{\Omega }_i ) + 2p_i ^{\prime} ({\bf M}
(t),{\bf H}_i (t)) \cdot y_i ^{\prime} (t|{\Omega }_i )\nonumber\\
&& +\, p_i ({\bf M}(t),{\bf H}_i (t)) \cdot y_i ^{\prime\prime} (t|{\Omega }_i ) - c_i ^{\prime\prime}
({\bf w}(t)^T {\bf x}_i (t)) < 0.
\end{eqnarray}
The necessary condition (equation 2) generally represents our PMR. Note that for the sufficient condition to hold, the slope of the value of the marginal product, hence the producer's derived demand for time feeding the animal, need only be more negatively sloped than the marginal factor costs of production. Therefore, an optimal marketing time for the animal can be derived even if marginal factor costs decline over time as would be the case of concave consumption (Tedeschi et al., Reference Tedeschi, Fox and Baker2003, p. 26). Due to the dynamics of output prices, input prices, and input quantities, multiple locally optimal points may occur. However, only one point will satisfy both equations (2) and (3) globally.
4. Data Description
We use existing data from the Mississippi Farm to Feedlot Program, which contain individual performance data for approximately 2,700 head of cattle. The Mississippi Farm to Feedlot Program was established in 1993 to evaluate feedlot and carcass performance for calves produced in Mississippi and to provide educational information to Mississippi beef cattle producers regarding retained ownership as a marketing alternative (Parish et al., Reference Parish, Smith and Vann2012). It often serves as an introduction to cattle finishing and harvest production and marketing systems for these producers. The program is coordinated by the Mississippi State University Extension Service.
The data for this analysis were collected from 2005 to 2011 and include dates and animal weights recorded at four different points during the feeding process. Of the 2,700 head in the original data series, only 1,701 had all four weights recorded at the time they were (1) delivered, (2) moved out of the warm-up pen (i.e., on-test weight), (3) reimplanted, and (4) harvested. Visual back fat estimates for each animal were conducted by trained personnel to determine the harvest date (according to EPMS). Table 1 reports the descriptive statistics for the cattle with all four body weights recorded. The delivery weights ranged from 380 to 1,116 pounds (mean 709.07, standard deviation 107.98). Harvest weights ranged from 950.95 to 1,599.97 pounds (mean 1242.64, standard deviation 151.20). Back fat at harvest averaged 0.44 inches (0.13 standard deviation) indicating the personnel were well trained at implementing the EPMS.
Table 1. Descriptive Statistics

Note: DOF, days on feed.
Also included in the data are aggregate production costs, both per head and per feeding group. Daily production costs were calculated by summing the total cost of yardage, feed consumption, and medication for each animal and dividing by the number of days each animal was on feed. Though cattle were managed in feeding groups, individual feed consumption was estimated from the feeder's closeout invoices based on composition of gain (lean vs. fat) using the Cattle Value Discovery System (e.g., Perry and Fox, Reference Perry and Fox1997; Tedeschi et al., Reference Tedeschi, Fox and Baker2003, Reference Tedeschi, Fox, Baker and Kirschten2006). The estimated average total variable costs per day are reported in Table 1. These costs averaged $2.08 per day ($0.31 standard deviation) with extremes ranging from $1.22 and $3.57 per day.
Finally, weekly fed cattle cash prices were obtained from the USDA Agricultural Marketing Service (AMS) Five Area Weekly Weighted Average Direct Slaughter Cattle report (USDA, AMS, 2013a). Descriptive statistics for the price data are also included in Table 1 and represent weekly prices from January 1, 2005, through December 31, 2011.
5. Growth Modeling and Profit Estimation
In the first part of this section, we analyze the Verhulst logistic growth function, which is the most common life-cycle growth equation used in both biological and economic sciences (Tsoularis and Wallace, Reference Tsoularis and Wallace2002). From this we estimate dynamic marginal physical product functions for each animal. As we will demonstrate in “Dynamic Growth Functions,” because cattle feeders do not normally know the age of the animal they purchase, adjustments must be made to the life-cycle model for applicability in the cattle feeding industry.
Next, we describe the empirical methodology used to estimate the parameters of the body weight function that will be substituted into the estimated profit model. To conclude this section, we describe a simplified version of the profit model depicted in equation (1) that was used to determine the profit maximizing harvest dates.
5.1. Dynamic Growth Functions
Estimation of the profit model depicted in equation (1) begins with the choice of a functional form of growth (equation of motion) and corresponding weight function,
![]() $y_i (t|{\Omega }_i ) \in Y$
, followed by estimation of the respective parameters,
$y_i (t|{\Omega }_i ) \in Y$
, followed by estimation of the respective parameters,
![]() ${\Omega }_i$
. We begin with an example of the classic Verhulst life-cycle logistic growth model (LC)
${\Omega }_i$
. We begin with an example of the classic Verhulst life-cycle logistic growth model (LC)
where
![]() $\frac{{dy_i (t)}}{{dt}}$
is the instantaneous rate of weight gain at any point in age (time) with initial condition
$\frac{{dy_i (t)}}{{dt}}$
is the instantaneous rate of weight gain at any point in age (time) with initial condition
![]() $y_i (0) = \frac{{m_i }}{{1 + \gamma _i }}$
(birth weight). Live weights,yi
(t), are the observed as the animal ages (time) t > 0; ki
∈ K > 0 is an efficiency (growth constant) parameter; γ
i
∈ Γ > 0 is a phenotypic adjustment factor (genetic potential) parameter; and mi
∈ M > yi
(0) ∈ Y(0) is the maturity weight parameter asymptotically approached as t → ∞. Equation (4) states that the rate of growth is proportional to the body weight in the current time period and the difference between the current and mature body weight. The corresponding sigmoidal LC weight function can be found by integrating the differential equation (4) resulting in
$y_i (0) = \frac{{m_i }}{{1 + \gamma _i }}$
(birth weight). Live weights,yi
(t), are the observed as the animal ages (time) t > 0; ki
∈ K > 0 is an efficiency (growth constant) parameter; γ
i
∈ Γ > 0 is a phenotypic adjustment factor (genetic potential) parameter; and mi
∈ M > yi
(0) ∈ Y(0) is the maturity weight parameter asymptotically approached as t → ∞. Equation (4) states that the rate of growth is proportional to the body weight in the current time period and the difference between the current and mature body weight. The corresponding sigmoidal LC weight function can be found by integrating the differential equation (4) resulting in
One limitation of any life-cycle growth function is that the age of animal at time t must be known. However, cattle feeders rarely know the age of the animals they feed. Consistent with the producer's lack of information, of the 1,701 head of usable data reported in Table 1, only 592 of the Mississippi cattle included birth date. Furthermore, convergence of three parameters during nonlinear estimation is more difficult when there are limited observations. Recognizing the producer's lack of information, and to make better use of our data, equation (4) can be modified to what we refer to as a days-on-feed growth model (DOFGM),
and the initial condition set as
![]() $y_i (0) = y_{0i} > \frac{{m_i }}{{1 + \gamma _i }}$
. In this model, y
0i
is the delivery weight of an age-unknown animal. Therefore, equation (6) states that the rate of growth is proportional to the difference between the observed weight at any given time (t) and a fixed limit or maturity weight. This type of growth function is, therefore, a limited growth function. Integrating the differential equation (6) results in the corresponding DOFGM weight function,
$y_i (0) = y_{0i} > \frac{{m_i }}{{1 + \gamma _i }}$
. In this model, y
0i
is the delivery weight of an age-unknown animal. Therefore, equation (6) states that the rate of growth is proportional to the difference between the observed weight at any given time (t) and a fixed limit or maturity weight. This type of growth function is, therefore, a limited growth function. Integrating the differential equation (6) results in the corresponding DOFGM weight function,
Note, however, that this functional form is not sigmoidal, but rather a quasi-concave and degenerative growth path.
Owens et al. (Reference Owens, Gill, Secrist and Coleman1995) pointed out an interesting issue related to our fed cattle growth models. They defined maturity weight as that point when the animal reaches a plateau of protein mass and noted that the animal can continue growing in live weight due to continued fat deposition. However, maintaining an extremely heavy animal that has been in a commercial feedlot setting is likely not sustainable due to the potential of subclinical and acute acidosis from consuming a high-energy diet for extended periods of time. Acidosis has been linked to laminitis (also caused by excess weight bearing on feet and legs) and rumen degeneration (Nagaraja, Reference Nagaraja2007). Therefore, the estimated maturity weight parameter must be constrained to a feasible plateau in both protein and fat deposition, in conjunction with the instantaneous rate of change parameter, as simply shape parameters.
5.2. Empirical Estimation of the Weight Function
Individual nonlinear parameters
![]() $\widehat{\Omega} _i = \{ \widehat{k}_i ,\widehat{m}_i ,\widehat{\gamma} _i \}$
for the LC and
$\widehat{\Omega} _i = \{ \widehat{k}_i ,\widehat{m}_i ,\widehat{\gamma} _i \}$
for the LC and
![]() $\widehat{\Omega} _i = \{ \widehat{k}_i ,\widehat{m}_i \}$
for the DOFGM weight functions (equations 5 and 7) are estimated using the nonlinear least squares procedure (Lopez et al., Reference Lopez, France, Gerrits, Dhanoa, Humphries and Dijkstral2000). Maturity weight must be estimated as there is no known research conducted to give us guidance as to the mature live weight of a feedlot animal.
$\widehat{\Omega} _i = \{ \widehat{k}_i ,\widehat{m}_i \}$
for the DOFGM weight functions (equations 5 and 7) are estimated using the nonlinear least squares procedure (Lopez et al., Reference Lopez, France, Gerrits, Dhanoa, Humphries and Dijkstral2000). Maturity weight must be estimated as there is no known research conducted to give us guidance as to the mature live weight of a feedlot animal.
Our estimation strategy uses an initial Gauss-Newton grid search to find adequate starting values of the parameters to be estimated. We then use the Marquardt gradient search method (Marquardt, Reference Marquardt1963) to guide the grid search for the parameters that lead to the minimized sum of squared errors (SSE). When convergence difficulties arose, we incorporated other common methods, the David-Fletcher-Powell and Broyden-Fletcher-Goldfab-Shanno methods (Greene, Reference Greene2003). The key assumptions of these procedures were that model errors are homoscedastic and uncorrelated with zero mean. The primary objective for evaluating the estimated growth functions was robustness of fit, as these results were pivotal in the estimation of the optimal market timing. The estimated LC and the DOFGM weight functions are compared by how well each minimizes the SSE or, more importantly, how well they predict live weight within the relevant region of market timing.
When estimating the LC growth model (equation 4) via the body weight function (equation 5), though the birth date was known, the initial condition, birth weight, was unknown. We assume a birth weight of 80 pounds for Mississippi cattle (Parish et al., Reference Parish, Smith, Parish, Best and Boland2009).Footnote 3 The estimated LC weight function, therefore, provides predictions for the birth weight and all four feedlot weights. The DOFGM model, however, treats the feedlot delivery weight,y 0i , as exogenous and predicts only the three remaining feedlot weights.
5.3. Profit Maximization Rule
To maintain focus on the use of nonlinear dynamic growth functions and recognize our data's limitations, we make several simplifications to the general model presented in equation (1). First, we do not account for dynamic price processes (i.e., changes in M(t) and H i (t)). Instead, we assume the producer makes a myopic marketing decision in relation to output price as opposed to forming an unobservable or proposed price expectation path; therefore, p′ i (M(t), H i (t)) = 0 and, by extension, p′′ i (M(t), H i (t)) = 0. We further assume the output price observed by the producer is competitively determined pi ∈ P. The next simplification is required as a restriction of the data. Production cost data are provided only at the end of the feeding period, and, therefore, we treat marginal factor costs of production as constant, resulting in c′ i (w(t) T x i (t)) = 0 and, by extension, c′′ i (M(t), H i (t)) = 0. Because of this data restriction, we cannot account for dynamic feed consumption or feed input prices. However, we later demonstrate that none of these simplifications/restrictions violate either the necessary nor sufficient conditions provided in equations (2) and (3).
Though the cattle in the data set were sold on a carcass merit basis, the growth functions specified are for live weight. As such, the marketing method used in our PMR is a live cattle spot market transaction for each animal. Furthermore, we do not account for output price paths, and we analyze transactions only within the marketing window, 950(t) ⩽ y(t) ⩽ 1, 450(t). This marketing window represents when the animal is expected to weigh between 950 and 1,450 pounds. Assuming a 63% yield, this results in a corresponding carcass weight range of 600 to 900 pounds, which are the minimum and maximum live weights that will not result in extreme price discounts applied to light- and heavyweight carcasses (USDA, AMS, 2013b).Footnote 4 Allowing for live/carcass weights outside the marketing window would result in discontinuous and unstable predictions of the optimal harvest date that we leave for future research addressing the dynamics of output prices. Finally, to test the robustness of opportunity cost results, we compare three plausible cash output prices observed within each animal's marketing window,pip ∈ (min, mean, max).
As a result of the simplifications, the general form of the estimated profit equations we simulate per animal reduces to
where w(h)
T
x
i
(h) ≡ wi
is the animal's average total daily variable costs calculated at the actual harvest date t = h. The variable costs include daily yardage, feed, and medicine charges. We note again that this is only an estimate of cost as daily individual feed consumption is unobservable in commercial feeding operations. Substitution of the estimated parameters
![]() ${\bf \hat \Omega }_i $
into growth equations (5) and (7) and subsequent substitutions into the profit function (equation 8) results in our two simulated profit functions
${\bf \hat \Omega }_i $
into growth equations (5) and (7) and subsequent substitutions into the profit function (equation 8) results in our two simulated profit functions
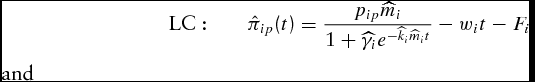 \begin{equation}
{\rm LC:}\quad \quad \hat \pi _{ip} (t) = \frac{{p_{ip} \widehat{m}_i }}{{1 + \widehat{\gamma} _i e^{ - \widehat{k}_i \widehat{m}_i t} }} - w_i t - F_i\end{equation}
and
\begin{equation}
{\rm LC:}\quad \quad \hat \pi _{ip} (t) = \frac{{p_{ip} \widehat{m}_i }}{{1 + \widehat{\gamma} _i e^{ - \widehat{k}_i \widehat{m}_i t} }} - w_i t - F_i\end{equation}
and
where each profit function is constrained within in the marketing window.
The corresponding unconstrained necessary condition for the simulated LC model is
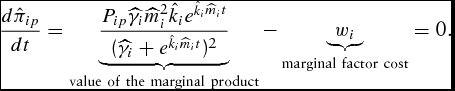 \begin{equation}
\frac{{d\hat \pi _{ip} }}{{dt}} = \underbrace {\frac{{P_{ip} \widehat{\gamma} _i \widehat{m}_i^2 \hat k_i e^{\hat k_i \widehat{m}_i t} }}{{( {\widehat{\gamma} _i + e^{\hat k_i \widehat{m}_i t} } )^2 }}}_{{\rm value\ of\ the\ marginal\ product}} - \underbrace {w_i }_{{\rm marginal\ factor\ cost}} = 0.\end{equation}
\begin{equation}
\frac{{d\hat \pi _{ip} }}{{dt}} = \underbrace {\frac{{P_{ip} \widehat{\gamma} _i \widehat{m}_i^2 \hat k_i e^{\hat k_i \widehat{m}_i t} }}{{( {\widehat{\gamma} _i + e^{\hat k_i \widehat{m}_i t} } )^2 }}}_{{\rm value\ of\ the\ marginal\ product}} - \underbrace {w_i }_{{\rm marginal\ factor\ cost}} = 0.\end{equation}
Solving equation (11) for the unconstrained optimal marketing time results in
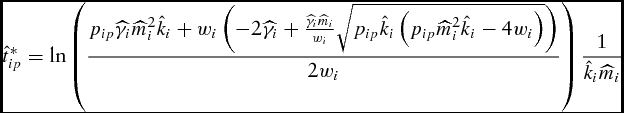 \begin{equation}
\hat t_{ip}^* = \ln \left( {\frac{{p_{ip} \widehat{\gamma} _i \widehat{m}_i ^2 \hat k_i + w_i \left( { - 2\widehat{\gamma} _i + \frac{{\widehat{\gamma} _i \widehat{m}_i }}{{w_i }}\sqrt {p_{ip} \hat k_i \left( {p_{ip} \widehat{m}_i ^2 \hat k_i - 4w_i } \right)} } \right)}}{{2w_i }}} \right)\frac{1}{{\hat k_i \widehat{m}_i }}\end{equation}
\begin{equation}
\hat t_{ip}^* = \ln \left( {\frac{{p_{ip} \widehat{\gamma} _i \widehat{m}_i ^2 \hat k_i + w_i \left( { - 2\widehat{\gamma} _i + \frac{{\widehat{\gamma} _i \widehat{m}_i }}{{w_i }}\sqrt {p_{ip} \hat k_i \left( {p_{ip} \widehat{m}_i ^2 \hat k_i - 4w_i } \right)} } \right)}}{{2w_i }}} \right)\frac{1}{{\hat k_i \widehat{m}_i }}\end{equation}
and, more generally, satisfies the sufficient condition
![]() $\scriptsize\frac{{d^2 \pi _{iP} }}{{dt^2 }} = - \scriptsize\frac{{w_i }}{{p_{ip} }}\scriptsize\sqrt {p_{ip} k_i ( {p_{ip} m_i ^2 k_i - 4w_i } )} < 0$
for all conventional restrictions of output price, production cost, and growth parameters. Substitution of the optimal LC market timing (equation 12) into the weight function (equation 5) results in the feeder's simulated unconstrained optimal supply of live weight,
$\scriptsize\frac{{d^2 \pi _{iP} }}{{dt^2 }} = - \scriptsize\frac{{w_i }}{{p_{ip} }}\scriptsize\sqrt {p_{ip} k_i ( {p_{ip} m_i ^2 k_i - 4w_i } )} < 0$
for all conventional restrictions of output price, production cost, and growth parameters. Substitution of the optimal LC market timing (equation 12) into the weight function (equation 5) results in the feeder's simulated unconstrained optimal supply of live weight,
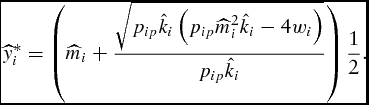 \begin{equation}
\widehat{y}_i^* = \left( {\widehat{m}_i + \frac{{\sqrt {p_{ip} \hat k_i \left( {p_{ip} \widehat{m}_i ^2 \hat k_i - 4w_i } \right)} }}{{p_{ip} \hat k_i }}} \right)\frac{1}{2}.\end{equation}
\begin{equation}
\widehat{y}_i^* = \left( {\widehat{m}_i + \frac{{\sqrt {p_{ip} \hat k_i \left( {p_{ip} \widehat{m}_i ^2 \hat k_i - 4w_i } \right)} }}{{p_{ip} \hat k_i }}} \right)\frac{1}{2}.\end{equation}
Given that the animal is to be marketed within the marketing window to avoid steep discounts, the censored optimality condition is
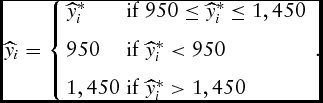 \begin{equation}
\widehat{y}_i = \left\{ \begin{array}{ll}
\widehat{y}_i^*& {\rm if\ }950 \le \widehat{y}_i^* \le 1,450 \\[7pt]
950&{\rm if\ }\widehat{y}_i^* < 950 \\[7pt]
1,450&{\rm if\ }\widehat{y}_i^* > 1,450
\end{array} \right..\end{equation}
\begin{equation}
\widehat{y}_i = \left\{ \begin{array}{ll}
\widehat{y}_i^*& {\rm if\ }950 \le \widehat{y}_i^* \le 1,450 \\[7pt]
950&{\rm if\ }\widehat{y}_i^* < 950 \\[7pt]
1,450&{\rm if\ }\widehat{y}_i^* > 1,450
\end{array} \right..\end{equation}
The corresponding unconstrained simulated necessary condition for the DOFGM model is
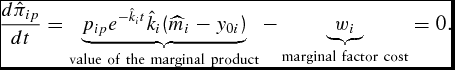 \begin{equation}
\frac{{d\hat \pi _{ip} }}{{dt}} = \underbrace {p_{ip} e^{ - \hat k_i t} \hat k_i (\widehat{m}_i - y_{0i} )}_{{\rm value\ of\ the\ marginal\ product}} - \underbrace {w_i }_{{\rm marginal\ factor\ cost}} = 0.\end{equation}
\begin{equation}
\frac{{d\hat \pi _{ip} }}{{dt}} = \underbrace {p_{ip} e^{ - \hat k_i t} \hat k_i (\widehat{m}_i - y_{0i} )}_{{\rm value\ of\ the\ marginal\ product}} - \underbrace {w_i }_{{\rm marginal\ factor\ cost}} = 0.\end{equation}
Solving equation (15) for the unconstrained simulated optimal marketing time results in
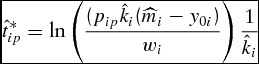 \begin{equation}
\hat t_{ip}^* = \ln \left( {\frac{{(p_{ip} \hat k_i (\widehat{m}_i - y_{0i} )}}{{w_i }}} \right)\frac{1}{{\hat k_i }}\end{equation}
\begin{equation}
\hat t_{ip}^* = \ln \left( {\frac{{(p_{ip} \hat k_i (\widehat{m}_i - y_{0i} )}}{{w_i }}} \right)\frac{1}{{\hat k_i }}\end{equation}
and, more generally, satisfies the sufficient condition as
![]() $\frac{{d^2 \pi _i }}{{dt^2 }} = - w_i k_i < 0$
for all conventional restrictions on production cost and the growth parameter. Substitution of the optimal DOFGM market timing (equation 16) into the body weight function (equation 7) results in the feeder's simulated optimal supply of live weight
$\frac{{d^2 \pi _i }}{{dt^2 }} = - w_i k_i < 0$
for all conventional restrictions on production cost and the growth parameter. Substitution of the optimal DOFGM market timing (equation 16) into the body weight function (equation 7) results in the feeder's simulated optimal supply of live weight
Again, equation (16) follows the censoring condition (equation 14). Comparative statics reveal that under either growth function, feeders would supply larger animals when output price, efficiency, and maturity weight increase and when marginal factor costs decrease.
5.4. Estimated Opportunity Cost
Finally, we compare the PMR approach (choosingt* ip ) with that of the EPMS (observed t = hi ). To do so, we simply calculate the profit difference equation,
for three plausible conditional prices each animal could have received within its respective marketing window. For a direct comparison between the two marketing strategies, animals actually harvested below 950 and above 1,450 pounds are excluded.
6. Empirical Growth and Profit Results
6.1. Growth Models
In this section, we first compare the within-sample predictive capabilities of the LC and DOFGM weight models (equations 5 and 7) when animal age is known.Footnote 5 Of the initial 592 head with a reported birth date, 588 head fell in the marketing window. Second, we present the results of the DOFGM weight model for all cattle. Of the 1,701 head with all four weights recorded, 1,467 head fell within the marketing window.
Owens et al. (Reference Owens, Gill, Secrist and Coleman1995) indicated that average maturity weight of feedlot steers is 1,641. Maturity is defined as the feasible plateaus in both protein and fat deposition. During estimation, we find that constraining the maturity weight parameter within
![]() $1,200 \le \widehat{m}_i \le 1,800$
in both the LC and DOFGM models facilitates more consistent model convergence.Footnote
6
This boundary constraint is significant at conventional levels for 11% of the observations for the DOFGM (equation 7) model when applied to the cattle for which age was known, and 14% for the DOFGM model when applied to all cattle. This boundary is not significant for any of the observations in the LC model.
$1,200 \le \widehat{m}_i \le 1,800$
in both the LC and DOFGM models facilitates more consistent model convergence.Footnote
6
This boundary constraint is significant at conventional levels for 11% of the observations for the DOFGM (equation 7) model when applied to the cattle for which age was known, and 14% for the DOFGM model when applied to all cattle. This boundary is not significant for any of the observations in the LC model.
Table 2 reports the results of the estimated parameters and the average mean squared errors (MSEs) for both the LC and DOFGM weight models for comparable animals. We find that the average MSE for the LC weight model is larger than the DOFGM weight model (2,140 vs. 1,546). On this metric alone, the DOFGM appears to outperform the LC across individuals. However, because the LC is estimating two more body weights per animal than the DOFGM weight model, an inflated MSE is expected. A more direct and important comparison is how well the two models predict each animal's observed weight within the marketing window.
Table 2. Estimation Results Comparison for Known Birth Date Cattle (N = 588)

Note: DOFGM, days-on-feed growth model; LC, life-cycle logistic growth model.
a
![]() $\widehat{k}_i$
is a unitless functional shape parameter.
$\widehat{k}_i$
is a unitless functional shape parameter.
We now focus our attention on the within-sample predictive capabilities of both the LC and DOFGM weight models in regard to the final and reimplant weights. The reason being is that these weights fall within the marketing window, the region where accurate predictions are the most important for later estimations of the optimal marketing time. The results depicted in Table 3 are the average mean deviation errors and root mean square errors (RMSEs) for each predicted weight per model. As can be seen, on average, both the LC and DOFGM models overpredict the reimplant weight (0.72% and 1.84% error, respectively). Also, both models underpredict final weight on average (0.64% and 1.35% error, respectively). These results could be due to a growth regime shift after reimplanting or the long number of days between reimplant and slaughter for the lightweight cattle (Table 1). When considering the standard deviations in prediction errors, both models predict the reimplant and final weights rather well, considering the large degree in variability of live weights at any given time. For instance, postfasting fill (the weight of the digestive tract contents) for feedlot animals has been found to range from 5% to 11% percent within this body weight range (Owens et al., Reference Owens, Gill, Secrist and Coleman1995).Footnote 7 The LC and DOFGM models predict 96% and 85% of the cattle within 3% of actual harvest body weight, respectively. However, some cattle weights are not predicted well when looking at the minimum and maximum mean error prediction. Finally, the RMSEs for the LC and DOFGM weight models are comparable for the two weights that fell within the marketing window (reimplant and harvest weights). However, when considering both the smaller mean deviations and comparable RMSEs, it appears that the LC model generally outperforms the DOFGM. This result indicates the power of more information (age and body weight) and a greater degree of model flexibility (number of parameters).
Table 3. Estimated Weight Error Comparison

Note: DOFGM, days-on-feed growth model; LC, life-cycle logistic growth model; RMSE, root mean square error.
a A 3% to 4 % error allowance for rumen fill is 25.02 to 33.36 pounds, calculated at the mean weight.
b A 3% to 4 % error allowance for rumen fill is 29.37 to 39.16 pounds, calculated at the mean weight.
c A 3% to 4 % error allowance for gut rumen is 37.26 to 49.68 pounds, calculated at the mean weight.
Finally, we present the results of the DOFGM model for all available observations in Table 3. Again, on average, the DOFGM model overestimates the reimplant weight (1.72% error) and underestimates the harvest body weight (1.29% error). These results are similar as those found using only animals of known body weight.
6.2. Profit Estimation
We first estimate LC and DOFGM profit equations (9) and (10) and solve for the optimal days on feed (
![]() $\hat t_{ip}^*$
) conditional on output price within the marketing window from equations (12) and (16). We then derive the estimated opportunity costs of EPMS and the days-on-feed differences for cattle of known age by equation (18). Table 4 reports these later results. Assuming each animal receives the mean price during its individual marketing window, the LC and DOFGM profit models indicate on average a $17.33 and $7.68 per head opportunity cost of the EPMS (or improvement using the PMR) method of marketing cattle, respectively. For all three prices within the marketing window, the LC model predicts a greater opportunity cost than the DOFGM model.
$\hat t_{ip}^*$
) conditional on output price within the marketing window from equations (12) and (16). We then derive the estimated opportunity costs of EPMS and the days-on-feed differences for cattle of known age by equation (18). Table 4 reports these later results. Assuming each animal receives the mean price during its individual marketing window, the LC and DOFGM profit models indicate on average a $17.33 and $7.68 per head opportunity cost of the EPMS (or improvement using the PMR) method of marketing cattle, respectively. For all three prices within the marketing window, the LC model predicts a greater opportunity cost than the DOFGM model.
Table 4. Life-Cycle Logistic Growth Model (LC) versus Days-on-Feed Growth Model (DOFGM): Dollars per Head Estimated Opportunity Cost of End-Point Marketing Strategy and Days-on-Feed (DOF) Differences

Note: Estimated opportunity cost is equation (18),
![]() $\widehat\varepsilon _{i|p} = \hat \pi _{ip} (t_{i|p}^* ) - \hat \pi _{i|p} (h_i )$
, which is the difference in estimated profit conditional on output price (p) if harvested at the optimal date (t*
i|p
) and actual harvest date (hi
). DOF difference is calculated as the difference between the optimum and actual harvest date conditional on output price, which is t*
i|p
− hi
.
$\widehat\varepsilon _{i|p} = \hat \pi _{ip} (t_{i|p}^* ) - \hat \pi _{i|p} (h_i )$
, which is the difference in estimated profit conditional on output price (p) if harvested at the optimal date (t*
i|p
) and actual harvest date (hi
). DOF difference is calculated as the difference between the optimum and actual harvest date conditional on output price, which is t*
i|p
− hi
.
Assuming that cattle are sold at the mean price during the marketing window, the LC and DOFGM profit models indicate on average that cattle were marketed 8.03 days late and 16.44 early, respectively, using the EPMS as shown in Table 4. Given that cattle are marketed on a weekly basis, these mean differences are minor. However, these results are misleading in that what is most important for maximizing the profitability of every individual animal lies in the respective standard deviation. As can be seen, roughly 68% of the cattle are marketed somewhere between a month and 2 months early or late, with a few extremes as much as half a year. Finally, it is not surprising that output price plays a large role in the optimal number of days on feed.
Figure 1a summarizes the estimated average opportunity costs of feeding longer or shorter than optimal using either the LC or DOFGM growth models. As can be seen, both models indicate there are sizable opportunity costs to the EPMS, generally more so using the LC growth model. Figure 1b shows the equivalent frequencies of observations that fall within each respective category. Whereas the average opportunity costs are greatest for those cattle that each model predicts were fed more than 80 days too short or too long, there are relatively few observations that fall within those ranges, especially for the DOFGM. In all, the results indicate there are significant gains in profitability using a PMR approach to market cattle. However, we caveat the magnitudes of these results as they are greatly dependent on accurately identifying and estimating the “true” underlying growth function for each animal. Given the results of model fit, we expect the DOFGM model underpredicts the “true” opportunity costs of EPMS.

Figure 1. Opportunity Cost Comparison and Frequencies between Life-Cycle Logistic Growth Model (LC) versus Days-on-Feed Growth Model (DOFGM) at Various Differences between Profit Maximization Rule (PMR) (Optimal) Days on Feed (DOF) and End-Point Marketing Strategy (EPMS) (Actual) DOF Using the Mean Cash Price, N = 588
In Table 4 we report the results from using all available cattle (1,467 head), whether the age is known (588 head) or not. Lacking such information, the only model we can appeal to is the DOFGM model. We find similar but lower results as those reported from the smaller data series.Footnote 8 Assuming cattle are sold at the mean price during their individual marketing window, the estimated opportunity cost of EPMS is $6.71 per head (down $0.97). At the same price, we now estimate that cattle are overfed 6.27 days, on average (down 10.17 days). Finally, the standard deviations for costs and days remain on par with the results from the smaller database. Figure 2 summarizes the estimated average opportunity costs of feeding longer or shorter than optimal and the frequency of observations using the DOFGM model. As can be seen, the results are on par with that of the smaller (age known) results.

Figure 2. Opportunity Cost and Frequencies at Various Differences between Profit Maximization Rule (PMR) (Optimal) Days on Feed (DOF) and End-Point Marketing Strategy (EPMS) (Actual) DOF Using the Mean Cash Price, N = 1,467
We now address the final question of whether EPMS is more or less appropriate for different classifications of cattle. We only consider delivery body weights as they proxy the age of the animal and the parameters of the growth function capture each animal's genetic potential, hence reducing the need to additionally segment breed types, and so forth. Table 5 presents the opportunity costs of EPMS broken down into delivery weight groups for all cattle. Again assuming each animal receives the mean price during their individual marketing window, we find that the opportunity costs of EPMS are positive for all weight classes, but the least for 500- to 700-pound animals. The results indicate that extremely lightweight animals (<500 pounds) and those from 700 to 900 pounds at delivery have a consistent opportunity cost ($7.26 to $7.54). However, regardless of output price, the greatest opportunity costs are for the heaviest animals. This indicates that very heavy cattle show the greatest area for potential profit improvement using a PMR approach (but carry with them the largest standard deviation). Furthermore, the results suggest that the heaviest cattle are overfed by 2 to 4 weeks on average, from minimum to maximum price. In all, the results suggest that heavy cattle placed on feed would benefit the most from a PMR marketing strategy.
Table 5. Days-on-Feed Growth Model (DOFGM): Dollars per Head Opportunity Cost of End-Point Marketing Strategy and Days-on-Feed (DOF) Differences for All Cattle by Delivery Weight Class (Pounds) (N = 1,467)

Note: Estimated opportunity cost is equation (18),
![]() $\widehat\varepsilon _{i|p} = \hat \pi _{ip} (t_{i|p}^* ) - \hat \pi _{i|p} (h_i )$
, which is the difference in estimated profit conditional on output price (p) if harvested at the optimal date (t*
i|p
) and actual harvest date (hi
). DOF difference is calculated as the difference between the optimum and actual harvest date conditional on output price, which is t*
i|p
− hi
. Standard deviations in parentheses.
$\widehat\varepsilon _{i|p} = \hat \pi _{ip} (t_{i|p}^* ) - \hat \pi _{i|p} (h_i )$
, which is the difference in estimated profit conditional on output price (p) if harvested at the optimal date (t*
i|p
) and actual harvest date (hi
). DOF difference is calculated as the difference between the optimum and actual harvest date conditional on output price, which is t*
i|p
− hi
. Standard deviations in parentheses.
7. Conclusions
This analysis contributes to the body of literature that has attempted to provide cattle feeders with information and decision tools to improve profitability in an otherwise thin-margin and high-risk business. It has long been acknowledged that within-pen (group) variation in cattle quality is an important contributing factor to lower profitability. However, some portion of cattle in the group will necessarily be over/underfed even if cattle are sorted into and sold as sufficiently like groups. The contribution of this analysis is that it incorporates individual dynamic growth models that could one day aid producers in optimally harvesting all animals. The methodology proposed appears to have merit as long as the costs of individual marketing (i.e., reduced pen space utilization and increased carcass variance) do not outweigh the benefits. Although the results of this research are specific to fed cattle production, the methodology used is applicable to any live animal production process.
Similar to past research, we are limited to an ex post analysis. The results indicate that an estimated increase in profitability from utilizing a dynamic profit maximizing approach is similar in magnitude to the improvement in revenue found by Koontz et al. (Reference Koontz, Hoag, Brethour and Walker2008), whereby they attempted to improve EPMSs through optimal, though costly, sorting procedures. Unlike past research in general, however, our approach utilizes information that is feasible and reliably measured in the current commercial setting. However, the optimal number and timing of live weights that should be taken during the production process to result in efficient and reliable predictions of cattle growth are yet to be determined.
The results presented by this research facilitate an important discussion pertaining to EPMSs. Our results imply that physiological attributes should be treated as dynamic outputs of production that increase (decrease) revenue, rather than as the sole target. In all, producers should realize that there is a time variant cost associated with adding body weight and improving carcass characteristics to livestock and that processors may or may not “truly” demand these improvements in value by way of sufficiently higher market prices. Processors, on the other hand, should realize that to solicit greater value products they must offer sufficiently higher prices to compensate the producer for the added costs. Under perfect foresight, we find that at low to average prices feeders generally hold on to cattle longer than our model would recommend and at high prices sell too quickly. However, these results are not necessarily indicative that producers are not attempting to maximize profits as we do not control for producer price expectations. Therefore, an area of future research should incorporate dynamic price expectations (prediction) and risk aversion.
An interesting by-product of our research pertains to the value of historical age and growth information for the feeder. We find that an age-dependent life-cycle growth model appears to modestly outperform a days-on-feed model derived to account for the fact that many, if not most, cattle are of unknown age when purchased by a cattle feeder. The debate over animal identification is well documented (e.g., Pendell et al., Reference Pendell, Brester, Schroeder, Dhuyvetter and Tonsor2010; Pouliot, Reference Pouliot2011; Pouliot and Sumner, Reference Pouliot and Sumner2008; Smith et al., Reference Smith, Tatum, Belk, Scanga, Grandin and Sofos2005; Tonsor and Schroder, Reference Tonsor and Schroeder2006). Many producers have viewed the added burden of maintaining individual identification as simply a cost. However, if historical age and growth information can be used to improve the profitability of the feeder, then by extension, the feeder would be willing to pay for such information. For instance, live cattle auctions can be described as a common value auction (Coatney et al., Reference Coatney, Shaffer and Menkhaus2012). It is a well-established principal in the common value auction literature that bids (price) increase as the noise of the true value's signal is reduced, hence mitigating the winner's curse (Krishna, Reference Krishna2002). Whether or not the actual value of animal identification is at least as great as the cost, we cannot say at this point. However, Pouliot (Reference Pouliot2011) found a processor willingness to pay premiums of 1.2% to 3.1% for Canadian steers when traceable animal identification is known. Our results imply that feeders, like processors, stand to reap benefits from having more complete information about the cattle entering their operations. Anecdotally, we show an average of between 1.4% and 1.9% increase in profitability for feeders if they know the age of feeder cattle. In all, our results indicate that animal identification is not strictly a cost.
We acknowledge that a fully specified profit maximization model for the livestock industry must include three dynamics: (1) growth, (2) prices, and (3) costs. For instance, future work would include estimating dynamic output price (expectations) and factor cost paths. It would also be of value to account for the functional relationships between carcass characteristics (value) and live body weight across time (e.g., Bruns et al., Reference Bruns, Pritchard and Boggs2004; May et al., Reference May, Dolezal, Gill, Ray and Buchanan1992). To extend our model to include dynamic marginal factor costs would require estimates of feed consumption and feed input prices over time. Furthermore, our modeling framework can easily be extended to provide ex ante and updateable predictions. For instance, using the results from ex post growth analyses, each animal can be assigned a growth function and set of parameters upon delivery based on observable and correlated animal characteristics. Throughout the feeding period, each animal's predicted growth function can be updated as cattle are individually weighed.
Finally, future research should include higher-frequency data and a wider variety of more flexible growth functions. Our attempts to estimate more flexible functions (larger number of shape parameters), such as the Gompertz, Richards, Brody, and Von Bertalanffy, were significantly hampered by their larger data requirements for consistent parameter convergence. As we demonstrate, the choice of the underlying growth function is the first step in accurately predicting market timing.









