1. Introduction
To increase sales, companies must either increase market participation or increase consumption intensity of existing customers. Market participation, market development, product development, and diversification are considered the four alternative product-market strategies to improve company performance (Ansoff, Reference Ansoff1957). Market participation has been widely studied in marketing literature (e.g., Applebaum, Reference Applebaum1966; Hadley et al., Reference Hadley, Mitchell, Sulmasy and Bloce1999; Sood, James, and Tellis, Reference Sood, James and Tellis2009). Researchers in applied economics often use discrete-choice models to estimate the effects of products’ and/or consumers’ attributes on the probability that a consumer would participate in a particular market (e.g., Blisard and Blaylock, Reference Bilsard and Blaylock1993; Chiang, Reference Chiang1991; Dubé, Reference Dubé2004; Eppstein et al., Reference Eppstein, Grover, Marshall and Rizzo2011). There is also broad literature on the study of food demand using the classical demand models of the Rotterdam model and the Almost Ideal Demand System (AIDS). Powell et al. (Reference Powell, Chriqui, Khan, Wada and Chaloupka2013) provided a systematic review of recent U.S. studies on price elasticity relating to consumer demand for sugar-sweetened beverages, fast food, and fruits and vegetables using these models. To our knowledge, no study has investigated the respective effect of price and income on market participation and consumption intensity of customers. The main reason for this is that the classical demand models use quantity as the dependent variable, and thus it is not possible to identify whether change in quantity is attributable to a change in purchase volume of existing customers or a change in the proportion of new customers in the market. Although discrete-choice models can be used to explain consumers’ decision as to whether to buy or not, these models usually have product attributes (e.g., fresh vs. frozen fish) and consumer attributes (e.g., consumer income, age, and education) as explanatory variables, instead of price and income variables.
The purpose of this article is to develop an extended Rotterdam model from the classical Rotterdam demand model, in which we measure the effects of economic factors such as price, expenditure, and advertising on the average purchase volume by existing customers and the proportion of customers in the market, separately. This study makes a methodological contribution by showing that the Rotterdam demand model can be extended to include both market participation and consumption intensity as dependent variables instead of using only quantity. In this application, we can estimate the different adjustments in purchase by current customers and potential customers in response to demand determinates. This will provide knowledge about how industries can adjust their market strategies according to market segments, and therefore increase efficiency of these strategies. For example, if the elasticity of market participation is larger than the elasticity of consumption intensity with respect to market promotion, this would suggest that promotion aimed at attracting new customers might be more effective than promotion aimed at increasing the purchase volume by current customers.
To illustrate its usefulness, the extended model is applied to household data on salmon purchases in France. The French salmon market is the world's largest salmon market. Many studies have used demand models to estimate demand elasticities in the main salmon markets, such as the European Union (EU), France, the United States, and Japan (e.g., Asche, Reference Asche1996; Asche, Bjorndal, and Salvanes, Reference Asche, Bjorndal and Salvanes1998; Asche et al., Reference Asche, Guttormsen, Sebulonsen and Sissenerd2005; Bjorndal, Salvanes, and Gordon, Reference Bjorndal, Salvanes and Gordon1994; Eales, Durham, and Wessells, Reference Eales, Durham and Wessells1997; Herrmann and Liu, Reference Herrmann and Lin1988; Herrmann, Mittelhammer, and Lin, Reference Herrmann, Mittelhammer and Lin1993; Wessells and Wilen, Reference Wessells and Wilen1993). The impacts of generic advertising implemented by the Norwegian Seafood Council (NSC) in most of the Norwegian salmon export markets have also been estimated from the results of some studies (e.g., Xie, Reference Xie2015; Xie, Myrland, and Kinnucan, Reference Xie, Myrland and Kinnucan2009). This extended Rotterdam model can be leveraged to further investigate how the demand determinants affect both market participation and consumption intensity of customers in the French salmon market.
The article is organized as follows: We start with a conceptual framework to illustrate how the Rotterdam model can be used to estimate the effect of traditional demand shifters on both market participation and consumption intensity. Next, the extended Rotterdam model is developed, followed by presentation of the data and estimation procedures. The estimated results are then discussed, and the article concludes with a summary of the main findings.
2. Conceptual FrameworkFootnote 1
Equation (1) is formulated to present the relationship in which companies increase product sales by increasing market participation of the product and/or sales to existing customers:
where q is quantity consumed, N is the number of potential customers, and NB is the number of actual consumers. Therefore, ![]() $\frac{q}{N}$ means consumption per capita;
$\frac{q}{N}$ means consumption per capita; ![]() $\frac{q}{{NB}}$ is consumption intensity of existing consumers, or the average weight of purchase (awp); and
$\frac{q}{{NB}}$ is consumption intensity of existing consumers, or the average weight of purchase (awp); and ![]() $\frac{{NB}}{N}$ is the ratio of actual consumers to total potential consumers, or market participation (mp). Per capita consumption, therefore, equals awp multiplied by mp.
$\frac{{NB}}{N}$ is the ratio of actual consumers to total potential consumers, or market participation (mp). Per capita consumption, therefore, equals awp multiplied by mp.
Consumption intensity and market participation could both be influenced by the same factors—namely, price (p), consumer income (y), and advertising (a), which is illustrated by
Taking the logarithmic total differential of equations (1) to (3) yields:
where ηp, ηy, and ηa are elasticities of market demand with respect to price, income, and advertising, respectively. These elasticities conform to the following identities:
Equations (8a)–(8c) indicate that the elasticity of demand with respect to any demand shifter i (i.e., price, income, or advertising) is the sum of the corresponding elasticity of consumption intensity (αi) and market participation (βi). Thus, given the estimates of any two of the elasticities in equations (8a)–(8c), the third elasticity can be obtained by addition or subtraction. For example, given estimates of consumption intensity elasticity αi and market participation elasticity βi, market demand elasticity ηi can obtained by addition. Furthermore, it can be implied that that if αi > βi, this suggests that marketers should focus on persuading current consumers to buy more. On the other hand, if αi < βi, it suggests that market strategies aimed at attracting new customers will be more effective. The elasticities in equations (5)–(7) will be estimated using the Rotterdam model.
3. Extended Rotterdam Model
The Rotterdam demand model (Barten, Reference Barten1964, Reference Barten1968, Reference Barten1977; Theil, Reference Theil1965, Reference Theil1975, Reference Theil1976) was selected because it allows us to implement both awp and mp as dependent variables in replacement of quantity. A similar extension of the AIDS model (Deaton and Muellbauer, Reference Deaton and Muellbauer1980) is not as straightforward. Following Brown and Lee (Reference Brown and Lee2010), the basic specification of the Rotterdam model incorporating advertising is
where the preference variable z in Brown and Lee (Reference Brown and Lee2010) is redefined here to be advertising (aj); while n is the number of goods in the system, and i indexes the equation. Here, ![]() ${w_i} = {{{p_i}{q_i}} / x}$ is the budget share for good i;pi and qi are market price and per capita consumption for good i; dln Q = ∑ni = 1widln qi is the Divisia volume index to measure the effect of real income; and θi = pi(∂qi/∂x) is the marginal propensity to consume the good i. πij = (pipj/x)sij is the Slutsky coefficient, where sij = (∂qi/∂pj + qj∂qi/∂x). This implies that the elasticities estimated by the Rotterdam model are Hicksian elasticities, or, in other words, compensated elasticities.
${w_i} = {{{p_i}{q_i}} / x}$ is the budget share for good i;pi and qi are market price and per capita consumption for good i; dln Q = ∑ni = 1widln qi is the Divisia volume index to measure the effect of real income; and θi = pi(∂qi/∂x) is the marginal propensity to consume the good i. πij = (pipj/x)sij is the Slutsky coefficient, where sij = (∂qi/∂pj + qj∂qi/∂x). This implies that the elasticities estimated by the Rotterdam model are Hicksian elasticities, or, in other words, compensated elasticities.
Substituting equation (4) into equation (9) results in
Therefore, the Rotterdam model can be further decomposed to distinguish consumption intensity (awp) and market participation (mp) as separate dependent variables:
 $$\begin{eqnarray}
{w_i}d\ln aw{p_i} & =& {\xi _{1i}} + {\vartheta _{1i}}d\ln \,Q + \sum\nolimits_j {\sigma {}_{1ij}} d\ln {p_j} + \sum\nolimits_j {\gamma {}_{1ij}} d\ln {a_j}\nonumber\\
{w_i}d\ln m{p_i} & =& {\xi _{2i}} + {\vartheta _{2i}}d\ln \,Q + \sum\nolimits_j {\sigma {}_{2ij}} d\ln {p_j} + \sum\nolimits_j {\gamma {}_{2ij}} d\ln {a_j}.
\end{eqnarray}$$
$$\begin{eqnarray}
{w_i}d\ln aw{p_i} & =& {\xi _{1i}} + {\vartheta _{1i}}d\ln \,Q + \sum\nolimits_j {\sigma {}_{1ij}} d\ln {p_j} + \sum\nolimits_j {\gamma {}_{1ij}} d\ln {a_j}\nonumber\\
{w_i}d\ln m{p_i} & =& {\xi _{2i}} + {\vartheta _{2i}}d\ln \,Q + \sum\nolimits_j {\sigma {}_{2ij}} d\ln {p_j} + \sum\nolimits_j {\gamma {}_{2ij}} d\ln {a_j}.
\end{eqnarray}$$
In the Rotterdam model, corresponding elasticities are calculated by the estimated parameters divided by the mean of the market share of good i in each equation. Hence the elasticities presented by equations (8a)–(8c) imply that the parameters in equation (10) and equation (11) have the following relationships:
Theory implies that the restrictions on the price and expenditure parameters in equation (10) are as follows (Brown and Lee, Reference Brown and Lee2010):
 $$\begin{eqnarray}
\sum\limits_{j = 1}^n {\pi _{ij}} & =& 0\quad \quad i = 1,2,...,n\,\left( {\hbox{Price homogeneity}} \right)\nonumber\\
\pi _{ij} & =& {\pi _{ji\,}}\quad i \ne j\,\left( {\hbox{Price symmetry}} \right)\nonumber\\
\sum\limits_{i = 1}^n {{\theta _i}} & =& 1,\,\sum\limits_{i = 1}^n {{\pi _{ij}}} = 1,\,{\rm and}\,\sum\limits_{i = 1}^n {{\omega _{ij}}} = 1\quad j = 1,2,...,n\,\left( {{\hbox{Adding up}}} \right)\!,
\end{eqnarray}$$
$$\begin{eqnarray}
\sum\limits_{j = 1}^n {\pi _{ij}} & =& 0\quad \quad i = 1,2,...,n\,\left( {\hbox{Price homogeneity}} \right)\nonumber\\
\pi _{ij} & =& {\pi _{ji\,}}\quad i \ne j\,\left( {\hbox{Price symmetry}} \right)\nonumber\\
\sum\limits_{i = 1}^n {{\theta _i}} & =& 1,\,\sum\limits_{i = 1}^n {{\pi _{ij}}} = 1,\,{\rm and}\,\sum\limits_{i = 1}^n {{\omega _{ij}}} = 1\quad j = 1,2,...,n\,\left( {{\hbox{Adding up}}} \right)\!,
\end{eqnarray}$$
where the advertising coefficients also conform to the adding-up restriction, because in order to satisfy the budget constraint, demand increase for some goods because of advertising must be offset by the demand decrease for other goods (Brown and Lee, Reference Brown and Lee2010, p. 889). Brown and Lee (Reference Brown and Lee2010) have also used Tintner-Ichimura-Basmann relationship as a source of restrictions on preference variables (Basmann, Reference Basmann1956; Ichimura Reference Ichimura1950–1951; Tintner, Reference Tintner1952). However, we did not impose these restrictions because different from Brown and Lee (Reference Brown and Lee2010) whereby advertising is assumed to affect demand by raising the marginal utility of the ith goods and therefore advertising enters the demand system as a modifier of the price terms (Xie, Myrland, and Kinnucan, Reference Xie, Myrland and Kinnucan2009), we have followed Xie, Myrland, and Kinnucan (Reference Xie, Myrland and Kinnucan2009) to assume advertising to affect the “baseline” pattern of consumption. Therefore, advertising was incorporated into the model via modification of the intercept terms.
Parameter relationships illustrated by equations (12a)–(12c) imply the corresponding theoretical restrictions in the awp and mp equation (11):
 $$\begin{eqnarray}
\sum\limits_{j = 1}^n {({\sigma _{1ij}} + {\sigma _{2ij}} )} &=& 0\quad i = 1,2,3\left( {{\hbox{Price homogeneity}}} \right)\nonumber\\
{\sigma _{1ij}} + {\sigma _{2ij}} &=& {\sigma _{1ji}} + {\sigma _{2ji}}\,\left( {{\hbox{Price symmetry}}} \right)\nonumber\nonumber\\
\sum\limits_{i = 1}^n {({\sigma _{1ij}} + {\sigma _{2ij}})} &=& 1\quad j = 1,2,3\nonumber\\
\sum\limits_{i = 1}^n {({\vartheta _{1i}} + {\vartheta _{2i}} )} &=& 1\nonumber\\
\sum\limits_{i = 1}^n {({\gamma _{1ij}} + {\gamma _{2ij}})} &=& 1\,( {{\hbox{Adding up}}}).
\end{eqnarray}$$
$$\begin{eqnarray}
\sum\limits_{j = 1}^n {({\sigma _{1ij}} + {\sigma _{2ij}} )} &=& 0\quad i = 1,2,3\left( {{\hbox{Price homogeneity}}} \right)\nonumber\\
{\sigma _{1ij}} + {\sigma _{2ij}} &=& {\sigma _{1ji}} + {\sigma _{2ji}}\,\left( {{\hbox{Price symmetry}}} \right)\nonumber\nonumber\\
\sum\limits_{i = 1}^n {({\sigma _{1ij}} + {\sigma _{2ij}})} &=& 1\quad j = 1,2,3\nonumber\\
\sum\limits_{i = 1}^n {({\vartheta _{1i}} + {\vartheta _{2i}} )} &=& 1\nonumber\\
\sum\limits_{i = 1}^n {({\gamma _{1ij}} + {\gamma _{2ij}})} &=& 1\,( {{\hbox{Adding up}}}).
\end{eqnarray}$$
Elasticities are calculated using the following formulas:
 $$\begin{eqnarray}
e_{ii}^{awp} &=& {\sigma _{1ii}}/{w_i}\quad \quad e_{ij}^{awp} = {\sigma _{1ij}}/{w_i}\,\left( {{\hbox{Price elasticities of}}\,awp} \right)\nonumber\\
e_i^{awp} &=& {\vartheta _{1i}}/{w_i}\,\left( {{\hbox{Expenditure elasticities of}}\,awp} \right)\nonumber\\
ADV_{ij}^{awp} &=& {\gamma _{1il}}/{w_i}\,\left( {{\hbox{Advertising elasticities of}}\,awp} \right)\nonumber\\
e_{ii}^{pene} &=& {\sigma _{2ii}}/{w_i}\quad e_{ij}^{pene} = {\sigma _{2ij}}/{w_i}\,\left( {{\hbox{Price elasticities of}}\,mp} \right)\nonumber\\
e_i^{pene} &=& {\vartheta _{2i}}/{w_i}\,\left( {{\hbox{Expenditure elasticity of}}\,mp} \right)\nonumber\\
ADV_{ij}^{pene} &=& {\gamma _{2ij}}/{w_i}\,\left( {{\hbox{Advertising elasticities of}}\,mp} \right)\nonumber\\
e_{ii}^* &=& ({\sigma _{1ii}} + {\sigma _{2ii}})/{w_i}\quad \quad e_{ij}^* = ({\sigma _{1ij}} + {\sigma _{2ij}})/{w_i}\,\left( {{\hbox{Price elasticity of demand}}} \right)\nonumber\\
e_i^* &=& ({\vartheta _{1ij}} + {\vartheta _{2ij}})/{w_i}\,\left( {{\hbox{Expenditure elasticity of demand}}} \right)\nonumber\\
ADV_{ij}^{} &=& ({\gamma _{1ij}} + {\gamma _{2ij}})/{w_i}\,\left( {{\hbox{Advertising elasticity of demand}}} \right).
\end{eqnarray}$$
$$\begin{eqnarray}
e_{ii}^{awp} &=& {\sigma _{1ii}}/{w_i}\quad \quad e_{ij}^{awp} = {\sigma _{1ij}}/{w_i}\,\left( {{\hbox{Price elasticities of}}\,awp} \right)\nonumber\\
e_i^{awp} &=& {\vartheta _{1i}}/{w_i}\,\left( {{\hbox{Expenditure elasticities of}}\,awp} \right)\nonumber\\
ADV_{ij}^{awp} &=& {\gamma _{1il}}/{w_i}\,\left( {{\hbox{Advertising elasticities of}}\,awp} \right)\nonumber\\
e_{ii}^{pene} &=& {\sigma _{2ii}}/{w_i}\quad e_{ij}^{pene} = {\sigma _{2ij}}/{w_i}\,\left( {{\hbox{Price elasticities of}}\,mp} \right)\nonumber\\
e_i^{pene} &=& {\vartheta _{2i}}/{w_i}\,\left( {{\hbox{Expenditure elasticity of}}\,mp} \right)\nonumber\\
ADV_{ij}^{pene} &=& {\gamma _{2ij}}/{w_i}\,\left( {{\hbox{Advertising elasticities of}}\,mp} \right)\nonumber\\
e_{ii}^* &=& ({\sigma _{1ii}} + {\sigma _{2ii}})/{w_i}\quad \quad e_{ij}^* = ({\sigma _{1ij}} + {\sigma _{2ij}})/{w_i}\,\left( {{\hbox{Price elasticity of demand}}} \right)\nonumber\\
e_i^* &=& ({\vartheta _{1ij}} + {\vartheta _{2ij}})/{w_i}\,\left( {{\hbox{Expenditure elasticity of demand}}} \right)\nonumber\\
ADV_{ij}^{} &=& ({\gamma _{1ij}} + {\gamma _{2ij}})/{w_i}\,\left( {{\hbox{Advertising elasticity of demand}}} \right).
\end{eqnarray}$$
4. Empirical Specification
The extended Rotterdam model will be applied to monthly household data of salmon consumption in France from 2006 through 2009. A dominant share of salmon in the French market is farmed Atlantic salmon. One important advantage of fish farming over capture fisheries is its ability to pace harvests in response to expected changes in price and costs. The greater flexibility in harvesting suggests an elastic supply. A Hausman test conducted by Xie, Myrland, and Kinnucan (Reference Xie, Myrland and Kinnucan2009) affirms the hypothesis that global salmon prices in a monthly model are predetermined. Moreover, France is just one segment of the world's salmon market. The supply to the French market is therefore more elastic. A large share of the smoked salmon in France is processed in eastern European countries by using raw fish imported from Norway, Scotland, and the Faroe Islands. When raw fish is farmed, and processed smoked salmon can be put in stock for a much longer period than fresh salmon, we think the price of smoked salmon is predetermined as well. We therefore assume the salmon prices in our study to be predetermined, and the ordinary Rotterdam model can be applied.
In the empirical model, we have n = 3 to index demand for fresh salmon, frozen salmon, and smoked salmon, respectively. In each equation, a single advertising variable is specified because among the main salmon producers/exporters, only the Norwegian salmon industry has promoted its product category through generic advertising. Advertising incorporated into the model is the expenditure of the generic advertising conducted by the NSC.
A large body of literature suggests that both current and past advertising efforts affect the purchase behaviors of consumers (e.g., Forker and Ward, Reference Forker and Ward1993; Schmit et al., Reference Schmit, Dong, Chung, Kaiser and Gould2002). At the same time, seasonality needs to be taken into account when monthly data are used. To conserve degrees of freedom and to mitigate any multicollinearity problems among the lagged advertising variables, the lag structure for advertising is constrained to follow a second-degree polynomial distribution (PDL) (Schmit et al., Reference Schmit, Dong, Chung, Kaiser and Gould2002), and seasonality is modeled by using harmonic variables (Doran and Quilkey, Reference Doran and Quilkey1972). The empirical modes to be estimated finally take the following form:
 $$\begin{eqnarray}
{w_i}d\ln {q_{i,t}} &=& {\delta _i} + {\theta _i}d\ln {Q_t} + \sum\limits_{j = 1}^3 {{\pi _{ij}}} d\ln {p_{j,t}} + \sum\limits_{m = 0}^2 {{\tau _{im}}d\ln {z_{m,t}}}\nonumber\\
&& +\, {h_{i1}}{H_{11,t}} + {h_{i2}}{H_{12,t}} + {h_{i3}}{H_{21,t}} + {\varepsilon _{i,t}}\nonumber\\
{w_i}d\ln aw{p_{i,t}} &=& {\xi _{1i}} + {\vartheta _{1i}}\,d\ln \,{Q_t} + \sum\limits_{j = 1}^3 {{\sigma _{1ij}}} d\ln {p_{j,t}} + \sum\limits_{m = 0}^2 {{\varphi _{1im}}} d\ln {z_{m,t}}\nonumber\\
&& +\, {h_{1i1}}{H_{11,t}} + {h_{1i2}}{H_{12,t}} + {h_{1i3}}{H_{21,t}} + {\varepsilon _{1i,t}}\nonumber\\
{w_i}d\ln m{p_{i,t}} &=& {\xi _{2i}} + {\vartheta _{2i}}\,d\ln \,{Q_t} + \sum\limits_{j = 1}^3 {{\sigma _{2ij}}} d\ln {p_{j,t}} + \sum\limits_{m = 0}^2 {{\varphi _{2im}}} d\ln {z_{m,t}}\nonumber\\
&& + {h_{2i1}}{H_{11,t}} + {h_{2i2}}{H_{12,t}} + {h_{2i3}}{H_{21,t}} + {\varepsilon _{2i,t}}\quad
i = \ 1,{\rm{ }}2,{\rm{ }}3,
\end{eqnarray}$$
$$\begin{eqnarray}
{w_i}d\ln {q_{i,t}} &=& {\delta _i} + {\theta _i}d\ln {Q_t} + \sum\limits_{j = 1}^3 {{\pi _{ij}}} d\ln {p_{j,t}} + \sum\limits_{m = 0}^2 {{\tau _{im}}d\ln {z_{m,t}}}\nonumber\\
&& +\, {h_{i1}}{H_{11,t}} + {h_{i2}}{H_{12,t}} + {h_{i3}}{H_{21,t}} + {\varepsilon _{i,t}}\nonumber\\
{w_i}d\ln aw{p_{i,t}} &=& {\xi _{1i}} + {\vartheta _{1i}}\,d\ln \,{Q_t} + \sum\limits_{j = 1}^3 {{\sigma _{1ij}}} d\ln {p_{j,t}} + \sum\limits_{m = 0}^2 {{\varphi _{1im}}} d\ln {z_{m,t}}\nonumber\\
&& +\, {h_{1i1}}{H_{11,t}} + {h_{1i2}}{H_{12,t}} + {h_{1i3}}{H_{21,t}} + {\varepsilon _{1i,t}}\nonumber\\
{w_i}d\ln m{p_{i,t}} &=& {\xi _{2i}} + {\vartheta _{2i}}\,d\ln \,{Q_t} + \sum\limits_{j = 1}^3 {{\sigma _{2ij}}} d\ln {p_{j,t}} + \sum\limits_{m = 0}^2 {{\varphi _{2im}}} d\ln {z_{m,t}}\nonumber\\
&& + {h_{2i1}}{H_{11,t}} + {h_{2i2}}{H_{12,t}} + {h_{2i3}}{H_{21,t}} + {\varepsilon _{2i,t}}\quad
i = \ 1,{\rm{ }}2,{\rm{ }}3,
\end{eqnarray}$$
where dln z m, t are the advertising variables computed by using the PDL structure. The Appendix illustrates how these advertising variables were constructed. H 11, t, H 12, t, and H 21, t are the harmonic variables, calculated as follows (Doran and Quilkey, Reference Doran and Quilkey1972; Gould, Cox, and Perali, Reference Gould, Cox and Perali1991):
 $$\begin{eqnarray}
{H_{1kt}} &=& COS({\lambda _k}t)\quad (k = 1,{\rm{ }}2)\ \quad t = \left( {1, \ldots ,T}\right)\!,\nonumber\\
{H_{21t}} &=& SIN({\lambda _1}t),
\end{eqnarray}$$
$$\begin{eqnarray}
{H_{1kt}} &=& COS({\lambda _k}t)\quad (k = 1,{\rm{ }}2)\ \quad t = \left( {1, \ldots ,T}\right)\!,\nonumber\\
{H_{21t}} &=& SIN({\lambda _1}t),
\end{eqnarray}$$
where
The estimated φ1im and φ2im are used to solve back for parameters γ1il and γ2il according to equation (A-7) in the Appendix, where γ1il and γ2il are the current and lag-period effects of advertising on consumption intensity and market participation, respectively.
The corresponding advertising elasticities are calculated using the following formulas:
 $$\begin{eqnarray}
ADV_{il}^{awp} &=& {\gamma _{1il}}/{w_i}\quad l = 0,1,...,13\,\left( {{\hbox{Short-run advertising elasticities of}}\,awp} \right)\nonumber\\
ADV_{il}^{pene} &=& {\gamma _{2il}}/{w_i}\,\left( {{\hbox{Short-run advertising elasticities of}}\,mp} \right)\nonumber\\
ADV_{il}^{} &=& ({\gamma _{1il}} + {\gamma _{2il}})/{w_i}\,\left( {{\hbox{Short-run advertising elasticity of demand}}} \right)\nonumber\\
ADV_i^{awp} &=& \sum\limits_{l = 0}^{13} {{\gamma _{1il}}} /{w_i}\quad l = 0,1,...,13\,( {{\hbox{Long-run advertising elasticities of }}}\nonumber\\
&& {awp} )\nonumber\\
ADV_i^{pene} &=& \sum\limits_{l = 0}^{13} {{\gamma _{2il}}} /{w_i}\,\left( {{\hbox{Long-run advertising elasticities of }}mp} \right)\nonumber\\
ADV_i^{} &=& \sum\limits_{l = 0}^{13} {({\gamma _{1il}} + {\gamma _{2il}}} )/{w_i}\,\left( {{\hbox{Long-run advertising elasticity of demand}}} \right).\nonumber\\
\end{eqnarray}$$
$$\begin{eqnarray}
ADV_{il}^{awp} &=& {\gamma _{1il}}/{w_i}\quad l = 0,1,...,13\,\left( {{\hbox{Short-run advertising elasticities of}}\,awp} \right)\nonumber\\
ADV_{il}^{pene} &=& {\gamma _{2il}}/{w_i}\,\left( {{\hbox{Short-run advertising elasticities of}}\,mp} \right)\nonumber\\
ADV_{il}^{} &=& ({\gamma _{1il}} + {\gamma _{2il}})/{w_i}\,\left( {{\hbox{Short-run advertising elasticity of demand}}} \right)\nonumber\\
ADV_i^{awp} &=& \sum\limits_{l = 0}^{13} {{\gamma _{1il}}} /{w_i}\quad l = 0,1,...,13\,( {{\hbox{Long-run advertising elasticities of }}}\nonumber\\
&& {awp} )\nonumber\\
ADV_i^{pene} &=& \sum\limits_{l = 0}^{13} {{\gamma _{2il}}} /{w_i}\,\left( {{\hbox{Long-run advertising elasticities of }}mp} \right)\nonumber\\
ADV_i^{} &=& \sum\limits_{l = 0}^{13} {({\gamma _{1il}} + {\gamma _{2il}}} )/{w_i}\,\left( {{\hbox{Long-run advertising elasticity of demand}}} \right).\nonumber\\
\end{eqnarray}$$
5. Data and Estimation Procedure
Europanel is a global partnership venture between GFK Panel Services and Kantar Worldpanel, two of the world's largest marketing information companies (Europanel, 2016). A data set of the French household purchase of salmon products between 2006:1 and 2009:13 was provided by Europanel via NSC. The data presented have been grossed by Europanel to the total population on a “monthly” level, with 4 weeks in a month. Therefore, there are 13 such “months” in a year. The original data set has the purchase value in euro, quantity, average weight of purchase (awp), and market participation (mp). Prices were calculated by dividing value by quantity. Each year, 20,000 households were selected by Europanel to represent the entire population of France. These households were randomly selected after basic family characteristics such as income, education, age, family size, and district of residence were controlled for. These households were asked to report what they had purchased each shopping trip by immediately scanning their purchased items using the machines provided by Europanel at their homes. Europanel updated 25% of the households each year, and the remaining 75% would continue their reports in the following year (Europanel, 2014). Advertising data between January 2005 and December 2009 were provided by NSC. We adjusted the advertising expenditure of 13 “months” by moving the weekly averages into a calendar month. The reason for including advertising expenditures for 2005 was to account for carryover effects of advertising on consumer purchases.
Table 1 shows that the mean purchase quantity of salmon products per 4 weeks were 1,829 metric tons (mt) of fresh salmon, 1,425 tons of smoked salmon, and 738 tons of frozen salmon. Smoked salmon is the most expensive at €21.62/kg, followed by frozen salmon at €12.24/kg, and fresh salmon at €11.48/kg. These numbers yield the expenditure shares of smoked, fresh, and frozen salmon at 49%, 36%, and 15%, respectively. From Table 1, we can see that the market participation for smoked salmon is actually quite low; only 28%, compared with 78% for fresh salmon and 63% for frozen salmon. This means that the large market share of smoked salmon is mainly attributed to high purchase volume of existing consumers. The average per household purchase by existing consumers of smoked salmon is 19.10 kg in contrast to 8.92 kg for fresh salmon and 4.50 kg for frozen salmon. NSC has, on average, spent €136,289 per 4 weeks to promote Norwegian salmon in the French market.
Table 1. Descriptive Statistics of Variables

Estimation was conducted in five steps: (a) We estimated the awp and mp equations in equation (16) in one systemFootnote 2 and quantity equations in another separate system. (b) The theoretical restrictions on both systems were then tested to see if they were compatible with the data. (c) The aforementioned two systems were reestimated with the theoretical restrictions imposed suggested by the test results. (d) The hypothesis of the parameter relationships between the two systems, presented by equations (12a)–(12c), were tested. (e) Finally, the elasticities in both the demand and the awp and mp systems were computed according to equations (15) and (18).
The models were estimated by statistical analysis software LIMDEP using seemingly unrelated regression (SUR) estimator. To avoid singularity in the variance-covariance matrix, in each of the three systems, first, the equation for fresh salmon was omitted. Then, to recover the parameters for the fresh salmon equation, we reestimated the systems with the equation for smoked salmon omitted. The results are identical if we recover the parameters in the fresh salmon equations by using the adding-up restriction specified in equation (14).
6. Results
The test results in Tables 2 and 3 show that in both the awp, mp system and the demand system, price homogeneity, and symmetry failed to be rejected when they were imposed separately. They were, however, rejected when imposed jointly. The theoretical restrictions on the demand system are considered the main reason that the estimation of a demand system is better than that of a single equation estimation. Furthermore, homogeneity and symmetry failed to be rejected when they were tested separately. We therefore estimated two systems with both price homogeneity and symmetry imposed.
Table 2. Tests of the Theoretical Restrictions in the awp and mp Model versus the Unrestricted Model

a Degrees of freedom for the tests are 2, 1, and 3 in the order of appearance.
Table 3. Tests of the Theoretical Restrictions in the Demand Model versus the Unrestricted Model

a Degrees of freedom for the tests are 2, 1, and 3 in the order of appearance.
The estimation results of both the demand system and the awp, mp system are satisfactory (Tables 4 and 5). More than half of the price and expenditure parameters were in-line with expected signs and significant at 10% or even lower significant levels. The estimated results of the harmonic variables show that seasonality is important in regard to French salmon consumption. TheR 2 ranged from 0.49 to 0.99, with the smoked salmon equations showing the highest fit. However, only one advertising parameter is statistically significant in the demand system, and three of them are significant in the awp, mp system. Although the results of the Wald tests suggest that the estimated advertising parameters are not jointly significant both in the demand system and the awp, mp system, we decided to keep them in the models because the main objective of the article is to discuss how the classical Rotterdam demand model can be further developed to have awp and mp as dependent variables. The insignificant results of long-term advertising effects should not preclude other researchers from using the extended model to investigate their advertising effects, as it is important in marketing studies. Furthermore, the effects of generic advertising are normally considered difficult to estimate because the level of generic advertising is usually tiny in relation to sales (Kinnucan and Zheng, Reference Kinnucan, Zheng, Kaiser, Alston, Crespi and Sexton2005). As reported in Table 1, the advertising intensity is only 0.23%, which means the advertising expenditure of NSC is only 0.23% of the total French household purchasing value of salmon. In addition, the Norwegian advertising is conducted to promote Norwegian salmon only, not salmon from other sources, and advertising is not only undertaken in grocery stores where most French households buy salmon, but also in restaurants and other places. Therefore, the fact that the estimated advertising effects are not reliable is not unexpected.
Table 4. Seemingly Unrelated Regression Estimates of Parameters for the Demand Model

Note: Asterisks (**, *) indicate significance at the 5% level and the 10% level, respectively; asymptotic t-ratio in parentheses.
Table 5. Seemingly Unrelated Regression Estimates of Parameters for the awp and mp Model

Note: Asterisks (**, *) indicate significance at the 5% level and the 10% level, respectively; asymptotic t-ratio in parentheses.
Mathematically, we can see that the sum of parameters associated with each variable in the mp and awp equations (Table 5) is almost equal to the corresponding parameters in the demand equations (Table 4). To further confirm this relationship, we tested the hypothesis of equations (12a)–(12c) and presented the results in Table 6. Here, t-tests were implemented because there is a single linear relationship existing between the parameters of the same explanatory variable (e.g.,dln pj) in the awp, mp and demand systems. The tested values are extremely close to zero, and t-ratios in the brackets are uniquely insignificant. These results show that the parameter relationships of equations (12a)–(12c) hold.
Table 6. Tests of the Parameter Relationships between the awp and mp Model and the Demand Model

Note: Numbers in parentheses are asymptotic t-ratios.
Although signs of the parameters in the Rotterdam framework are the same as the elasticities, they are not elasticities themselves. For a detailed discussion on the price, expenditure, and advertising effects on awp, mp measures and salmon demand, we focus on the elasticities, which are computed by the Wald test using equations (15) and (18). The elasticities in the demand and awp, mp systems are presented in Tables 7 and 8, respectively.
Table 7. Seemingly Unrelated Regression Estimates of Elasticities in the Demand Model

Notes: Asterisks (**, *) indicate significance at the 5% level and the 10% level, respectively; asymptotic t-ratio in parentheses. To make the table neat, we omitted the advertising parameters that are insignificant in all the equations. “-” means not significant in the specific equation
Table 8. Seemingly Unrelated Regression Estimates of Elasticities in the awp and mp Model

Notes: Asterisks (**, *) indicate significance at the 5% level and the 10% level, respectively; asymptotic t-ratio in parentheses. To make the table neat, we omitted the advertising parameters that are insignificant in all the equations. “-” means not significant in the specific equation.
6.1. Price Effect
Asche (Reference Asche1996) estimated the demand for salmon in the EU, using the AIDS model. The estimated compensated own-price elasticity in his study for the fresh salmon is −1.223. Those elasticities for frozen salmon and smoked salmon are not significantly different from zero. The price elasticities estimated in our study are also compensated elasticities. In the results of the demand system (Table 7), the own-price elasticities are negative and significant at the 5% level for both fresh and smoked salmon, but not for frozen salmon. The estimated own-price elasticity of fresh salmon is −1.203, consistent with the result given by Asche (Reference Asche1996). The insignificance of the own-price elasticity of frozen salmon also confirms the result found by Asche (Reference Asche1996). However, different from Asche (Reference Asche1996), we estimated a smoked salmon elasticity of −0.565. This is mainly explained by the data sources: Asche's study uses trade data, whereas our study uses household data. A considerate share of smoked salmon in the EU is processed in the EU with imported fresh salmon, which makes the import demand for smoked salmon smaller. The estimated cross-price elasticities indicate that in the French market, both frozen and smoked salmon are substitutes for fresh salmon, and more substitutions take place between fresh and smoked salmon.
As indicated by formulae (15), the same relationships between the parameters also exist between the elasticities. For example, own-price elasticity for fresh salmon can be identically decomposed to own-price elasticity in respect to households’ awp and mp, respectively. The estimated elasticities of the awp and mp are presented in Table 8. It shows that the price of fresh salmon affects households’ mp more than the awp of fresh salmon. Specifically, a 1% decline in the price of fresh salmon will increase the rate of the households that buy the fresh salmon by 0.76%, compared with an increasing average amount of each household's purchase by 0.44%. The estimated results of own-price elasticities of smoked salmon suggest that it affects the market participation only.
The cross-price elasticities of smoked salmon in the equations of fresh salmon awp and mp indicate that the strong substitute of smoked salmon for fresh salmon mainly happens on mp, not awp. A 1% decline in the smoked salmon price will decrease the percentage of households who buy fresh salmon by 1.028%. It, however, will not change the average amount of fresh salmon that each household buys. This result suggests that when smoked salmon prices decrease, French households will shift their purchase from fresh salmon to smoked salmon. However, it will not affect the amount they buy once they decide to stay within the fresh salmon market. The cross-price elasticities of fresh salmon in the equations of smoked salmon awp and mp suggest that the impact of fresh salmon price on households’ demand for smoked salmon is, however, somewhat equally contributed by its effect on the awp and mp.
6.2. Expenditure Effect
The estimated expenditure elasticity of fresh salmon in Table 7 suggests that household expenditure has no significant effect on the household's purchase of fresh salmon, which is not as expected, because not every family in France can easily afford to buy fresh salmon. The expenditure elasticities for frozen and smoked salmon are 0.421 and 1.884, respectively. This result is expected because smoked salmon in France is considered a luxury good and much more expensive than fresh and frozen salmon.
Expenditure effects on awp and mp are presented in Table 8. The effect of expenditure on fresh salmon awp is 0.144, which implies that the expenditure has a significant effect on the average number of households that buy, although overall, it has no significant effect on the quantity demanded. The effects of expenditures on frozen salmon and smoked salmon are relatively larger via the effect on mp, compared with the effect on awp.
6.3. Advertising Effect
For the advertising effect, we only report the estimated results significant at 10% or lower significance levels. Because only a couple of short-term elasticities are statistically significant, the joint significance of advertising elasticities was tested using the Wald test. The test results suggest that they are not jointly significant. This means the NSC advertising has no effect on the French household purchase of salmon in the long run, although it is estimated to have effects in the short run. The elasticities estimated in the demand system are all conditional elasticities, which means that the estimated advertising results only capture the effects of advertising on the distribution of household demand across the product forms included in the system, not the total demand for salmon. As discussed by Kinnucan and Myrland (Reference Kinnucan and Myrland2008), advertising might increase the total French household demand for salmon; therefore, the estimated effects of advertising might be understated.
Although advertising is found to have no significant effect in the long run, we still find it interesting to look at its short-term effects. Results in Table 7 indicate that advertising has a negative effect on the French household demand for fresh salmon, a positive effect for smoked salmon, and no significant effect for frozen salmon. The results of no effect for frozen salmon are beyond our expectation. The adding-up condition in the Rotterdam model means that with the expenditure on salmon held constant, any increase in demand for one salmon product must be met by a decrease in the demand for another salmon product. About 70% of the Norwegian salmon exported to the EU is fresh. Frozen salmon in the EU is either Pacific frozen salmon from Canada or Atlantic salmon from Chile. When the NSC promotes Norwegian salmon in France, consumers will potentially link the image of Norwegian salmon with fresh salmon or/and smoked salmon, as the latter is processed with imported fresh salmon. Thus, we would expect the NSC promotion will decrease consumer demand for frozen salmon. The negative effect on fresh salmon might be a direct result of the adding-up condition. Without violating budget constraints, an increase in demand for one salmon product must be at the cost of another. The estimated results in Table 7 indicate that most of the advertising effect occurs in the current “month” or next “month.” Although we specified the carryover effect of the advertising to lag over 13 “months,” the result is the same.
When advertising effects were decomposed to awp and mp effect, the estimated results in Table 8 indicate that overall advertising is effective in increasing the amount of salmon each household buys, but not in getting new consumers. The estimated advertising elasticity for fresh salmon (−0.024) is negative and three times larger in absolute value than the estimated advertising elasticity for smoked salmon (0.008). This suggests Norway's advertising in the French market redistributed demand away from fresh salmon toward smoked salmon. Whether the redistribution was welfare increasing for Norway's producers depends on whether the revenue gain from increased sales of its salmon used in the smoking industry was sufficient to offset the revenue loss from decreased sales of its salmon in the fresh market to cover advertising costs, an issue not addressed in this study.
7. Concluding Remarks
In this study, the Rotterdam model is extended to permit separate estimates of how consumption intensity and market participation respond to price, income, and other demand determinants such as market promotion. Specifically, the dependent variable in the Rotterdam model is shown to consist of two additive components: the proportional change in the average product weight consumed by existing consumers and the proportional change in the share of total consumers in the market who actually purchase the product. By doing so, we can estimate how demand determinants affect purchases by current customers and potential customers, separately. When such data are available, the extended Rotterdam model is useful in revealing more detailed information about market structure and thus improving the efficacies of industries’ marketing strategies. For example, this model helps marketers understand whether they should concentrate their market strategies on persuading existing customers to purchase more or on attracting new customers.
Applying the extended model on the French household demand for salmon, we find that salmon prices overall are more significant in affecting customers’ market participation than in affecting how much existing customers buy. In the short run, the NSC advertised successfully, triggering an increased purchase amount by existing customers, but it was not successful in getting new customers. New customers are usually important for an industry to expand its market share; therefore, the results suggest that in addition to keeping the loyalty of old customers, the NSC should adjust its advertising strategies in order to attract new customers.
Our statements regarding the French salmon market are based on the following findings: First, seven price elasticities are significant in the market participation equations, versus only three in the consumption intensity equations (Table 8). Second, the magnitudes of the price elasticities in the market participation equations are generally larger than the magnitudes of the corresponding price elasticities in the consumer intensity equations. The estimated parameters to capture the short-term advertising effects in consumption intensity equations are statistically significant, versus the insignificant corresponding estimated parameters of advertising in the market participation equations.
Some caution should be taken when interpreting the results of the Norwegian advertising. First, although the advertising is found to have effects in the short run, we failed to identify its long-run effects. The demand models only capture how advertising affects the distribution of the French households’ demand for the different product forms in question, but do not capture the result regarding how the advertising might increase the French households’ total demand for salmon. Third, it is difficult to draw a conclusion about the effectiveness of generic advertising conducted by the NSC, even if this advertising has a positive effect on the French household demand for smoked salmon at the cost of fresh salmon. Because salmon industries in the EU import the fresh Norwegian salmon as raw material from which to produce smoked salmon, the net benefit of the Norwegian salmon industry from its own promotional activities in France depends on the relative proportion of the imported Norwegian fresh salmon used directly as household meals and as raw materials for smoked salmon processing.
Appendix
Construction of the Advertising Variables
A general distributed lag model takes the following form:
 $$\begin{equation}
d{y_t} = \sum\limits_{l = 0}^L {{\omega _l}d\ln {a_{t - l}}} ,
\end{equation}$$
$$\begin{equation}
d{y_t} = \sum\limits_{l = 0}^L {{\omega _l}d\ln {a_{t - l}}} ,
\end{equation}$$
where dyt is the dependent variable in a model, a t − l is the advertising expenditure in current and lag periods, and ωl is fixed lag weight. In our study, dyt is the dependent variable of the Rotterdam model (widln qi) in equation (9), and a t − l is the advertising expenditure by the Norwegian Seafood Council in period t − l. Based on a review of the econometric literature, Clarke (Reference Clarke1976) concludes that 90% of the cumulative effect of advertising on sales of mature, frequently purchased, low-priced products occurs within 3 to 9 months of the advertisement. The data in our study have a periodicity of 4 weeks, which yields 13 periods in a year. Accordingly, we specified lag length l = 13 for the advertising variable in our model to make sure that the cumulative effect of advertising has been fully accounted for.
Following Schmit et al. (Reference Schmit, Dong, Chung, Kaiser and Gould2002), we approximated the lag weights by using a second-degree polynomial distributed lag structure. Restricting the weights to lie on a polynomial of second degree yields:
From equation (A-2), we have
 $$\begin{equation}
\sum\limits_{l = 0}^L {{\omega _{il}}d\ln {a_{t - l}}} = {\tau _{i0}}d\ln {z_0} + {\tau _{i1}}d\ln {z_1} + {\tau _{i2}}d\ln {z_2},
\end{equation}$$
$$\begin{equation}
\sum\limits_{l = 0}^L {{\omega _{il}}d\ln {a_{t - l}}} = {\tau _{i0}}d\ln {z_0} + {\tau _{i1}}d\ln {z_1} + {\tau _{i2}}d\ln {z_2},
\end{equation}$$
where 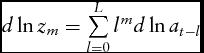 $d\ln {z_m} = \sum\limits_{l = 0}^L {{l^m}d\ln {a_{t - l}}} $, m = 0, 1, 2. The Rotterdam model in equation (9) then becomes
$d\ln {z_m} = \sum\limits_{l = 0}^L {{l^m}d\ln {a_{t - l}}} $, m = 0, 1, 2. The Rotterdam model in equation (9) then becomes
 $$\begin{equation}
{w_i}d\ln {q_i} = {\delta _i} + {\theta _i}d\ln Q + \sum\nolimits_j {\pi {}_{ij}} d\ln {p_j} + \sum\limits_{m = 0}^2 {{\tau _{im}}d\ln {z_m}} \quad \quad i = 1,2,..n
\end{equation}$$
$$\begin{equation}
{w_i}d\ln {q_i} = {\delta _i} + {\theta _i}d\ln Q + \sum\nolimits_j {\pi {}_{ij}} d\ln {p_j} + \sum\limits_{m = 0}^2 {{\tau _{im}}d\ln {z_m}} \quad \quad i = 1,2,..n
\end{equation}$$
The consumption intensity (awp) and market participation (mp) equations can accordingly be specified as
 $$\begin{eqnarray}
{w_i}d\ln aw{p_i} &=& {\xi _{1i}} + {\vartheta _{1i}}\,d\ln \,Q + \sum\nolimits_j {\sigma {}_{1ij}} d\ln {p_j} + \sum\limits_{m = 0}^2 {{\varphi _{1im}}} d\ln {z_m}\nonumber\\
{w_i}d\ln m{p_i} &=& {\xi _{2i}} + {\vartheta _{2i}}\,d\ln \,Q + \sum\nolimits_j {\sigma {}_{2ij}} d\ln {p_j} + \sum\limits_{m = 0}^2 {{\varphi _{2im}}d\ln {z_m}} .
\end{eqnarray}$$
$$\begin{eqnarray}
{w_i}d\ln aw{p_i} &=& {\xi _{1i}} + {\vartheta _{1i}}\,d\ln \,Q + \sum\nolimits_j {\sigma {}_{1ij}} d\ln {p_j} + \sum\limits_{m = 0}^2 {{\varphi _{1im}}} d\ln {z_m}\nonumber\\
{w_i}d\ln m{p_i} &=& {\xi _{2i}} + {\vartheta _{2i}}\,d\ln \,Q + \sum\nolimits_j {\sigma {}_{2ij}} d\ln {p_j} + \sum\limits_{m = 0}^2 {{\varphi _{2im}}d\ln {z_m}} .
\end{eqnarray}$$
The parameter relationships of advertising variables presented by equation (12c) suggest
According to equations (A-2) and (A-6), we have
 $$\begin{eqnarray}
{\gamma _{1il}} &=& {\varphi _{1i0}} + {\varphi _{1i1}}l + {\varphi _{1i2}}{l^2}\nonumber\\
{\gamma _{2il}} &=& {\varphi _{2i0}} + {\varphi _{2i1}}l + {\varphi _{2i2}}{l^2}.
\end{eqnarray}$$
$$\begin{eqnarray}
{\gamma _{1il}} &=& {\varphi _{1i0}} + {\varphi _{1i1}}l + {\varphi _{1i2}}{l^2}\nonumber\\
{\gamma _{2il}} &=& {\varphi _{2i0}} + {\varphi _{2i1}}l + {\varphi _{2i2}}{l^2}.
\end{eqnarray}$$
Equation (A-7) can be used to solve back for γ1il and γ2il based on the estimated φ1im and φ2im. γ1il and γ2il are the current and lag effects of the advertising on consumption intensity and market participation, respectively, and γ1il+γ1il=ωil, where ωil is the total effect of advertising on demand for the salmon product i. ωil divided by the mean of the expenditure share (wi) is the advertising elasticity for product i.










