1. Introduction
The U.S. Department of Agriculture (USDA) Risk Management Agency (RMA) established the Rainfall Index Annual Forage Program (RIAFP) in May 2013 with the goal of providing risk coverage for annual forage producers in the United States (USDA, RMA, 2013). Similar to the previously established Pasture, Rangeland, and Forage (PRF) insurance program (USDA, RMA, 2015b), this insurance product offers catastrophic risk (CAT) protection and buy-up coverage to a group of previously underserved producers (Campiche and Jones, Reference Campiche and Jones2014). Initially being tested as a pilot program in Texas, Oklahoma, Kansas, Nebraska, South Dakota, and North Dakota, this program covers annually planted crops that are used for livestock feed or fodder including grasses and mixed forages (ryegrass, sudan, etc.) and small grains (wheat, oats, etc.), among others (Campiche and Jones, Reference Campiche and Jones2014). As a new and relatively little-known program, a need exists to determine if the design of this program provides the intended risk protection. The objectives of this study are to measure the effectiveness of the RIAFP as a risk management tool for forage producers and to provide guidance to producers as to what choices to make when signing up for the RIAFP.
Because actual forage production is often difficult to measure and regulate, indemnity qualification for the program is based on interpolated precipitation within a producer's respective area or grid. This substitution will provide risk protection if forage yields are closely correlated with precipitation and should avoid the moral hazard and adverse selection that farm-level yield insurance would introduce if producers self-reported yield information. Moral hazard refers to the problem that occurs if producers alter their behavior after buying insurance in order to increase their likelihood of collecting indemnities (Goodwin, Reference Goodwin1994). Reducing potential moral hazard by using a variable other than actual yield could decrease the risk protection provided (Glauber, Reference Glauber2004; Nadolnyak and Vedenov, Reference Nadolnyak and Vedenov2013). Crop insurance programs based on a rainfall index were first implemented in 2007 with a pilot program for the PRF insurance program. The PRF program has since been joined by the Apiculture insurance program and the RIAFP. Each of these programs utilizes rainfall indices calculated from weather data collected by the National Oceanic and Atmospheric Administration (NOAA).
The RMA rainfall indices are based on weather data collected by NOAA and are designed to insure against declines in an index in each 0.25° latitude by 0.25° longitude grid (Shields, Reference Shields2015; USDA, RMA, 2014). Because the grids outnumber the weather data collection stations, a weighted average is calculated using the nearest four stations. The question of concern is, Does actual forage production follow the RMA rainfall indices closely enough to protect producers from production risk? There are two sources of basis risk: (1) correlation of the index with actual rainfall and (2) correlation of rainfall and forage yields.
Relatively little work has analyzed the use of the aforementioned rainfall indices in a crop insurance framework. Diersen, Gurung, and Fausti (Reference Diersen, Gurung and Fausti2015) discuss the use of rainfall indices in the PRF insurance program and use the rainfall indices provided by the RMA to determine which intervals producers should weight most. Using the RMA rainfall indices and county-level data, they found that the May–June and July–August periods should be weighted most heavily for perennial forage producers in South Dakota. Further, they conclude that producers would earn higher returns per acre with lower risk by participating in the subsidized insurance program than they would without participating.
Brooks et al. (Reference Brooks, Vandeveer, Volesky and Waters2014) and Vandeveer, Berger, and Stockton (Reference Vandeveer, Berger and Stockton2013) discuss the usefulness and implementation of rainfall index–based crop insurance programs for forage and livestock production in the United States. Maldonado (Reference Maldonado2011) analyzed the coverage-level choice producers face under a rainfall index–based crop insurance program and provides an in-depth overview of the rainfall index used in the RIAFP. From a different perspective, Nadolnyak and Vedenov (Reference Nadolnyak and Vedenov2013) examined whether a seasonal rainfall index or El Niño index are better predictors of forage yield in the southeastern United States. They found that it is possible for adverse selection to exist if the rainfall index is highly correlated with long-run weather forecasts. Breustedt, Bokusheva, and Heidelbach (Reference Breustedt, Bokusheva and Heidelbach2008) found that a weather index measure provides less risk reduction than a regional yield index for wheat producers in Kazakhstan.
The first purpose of our study is to determine whether the RIAFP provides the intended production risk coverage for annual forage growers. We analyze annual rye-ryegrass production at the Samuel Roberts Noble Foundation Red River Farm in Burneyville, Oklahoma, from 1974 to 2008. Annual ryegrass is the most widely used cool-season annual forage in the southeastern United States and is most often used to provide winter-grazing pasture for livestock (Parish et al., Reference Parish, Parish, Best and Saunders2012). Within the states covered by the RIAFP, cool-season annual forages are most often used as far south as Texas and as far north as southern Kansas (Reed, 1998). Burneyville, Oklahoma, is near the Oklahoma and Texas border and is central to the RIAFP region in which cool-season annual forages are planted. The data used include actual forage production over this time period at the same location as a weather station that has collected actual rainfall data since 1993. This data set is a relatively long series of data for continuous agronomic research and allows many years from which to consider the effectiveness of the design of the RIAFP. This may well be the only cool-season annual forage experiment with more than 20 years of data and an on-site weather station. To measure how well actual forage production follows the NOAA rainfall indices, we calculate the correlations between actual forage production, the rainfall index, and actual rainfall. Further, we estimate a linear model including other variables that might impact forage yield. We also perform ex post analyses of how often the RIAFP would have triggered an indemnity payment for the acreage in the data set and what the total payoffs would have been relative to the premiums paid.
Expected implications surround the applicability of establishing the RIAFP as a permanent and nationwide program. If forage yields show little correlation with the rainfall index, then a redesign of the insurance product to provide greater risk protection could be needed. Even if ineffective in reducing risk, the program can be viewed as a way of transferring income to a sector of agricultural producers generally underserved by subsidized risk products relative to other crops. Because the RIAFP is a relatively little-known program, this information could be useful for policy makers and for those in extension who may be asked about this program by growers.
1.1. Program Description
The RIAFP offers coverage to producers who annually plant crops used for livestock feed or fodder such as grazing, haying, haying/grazing, silage, and green chopping, among other purposes (USDA, Federal Crop Insurance Corporation [FDIC], RMA, 2015). Two types of risk protection are available: CAT coverage and buy-up coverage. CAT coverage is a fixed-level protection fully subsidized by the USDA and aims to provide protection against a particularly catastrophic event such as an extreme drought for forage producers. CAT coverage is available for all of the previously mentioned uses except for grazing. Additionally, producers have the option to purchase higher levels of risk coverage through buy-up coverage for any of the mentioned purposes for which they are required to pay only a portion of the premium. The forage insurance program relies on the previously defined rainfall index relative to the historical average of the index for any particular grid.
The RIAFP is similar to other insurance programs in that producers make a series of choices that influence the premium cost and coverage level for their operations (USDA, FDIC, RMA, 2013). First, the producer chooses the growing season and possible rainfall indices by choosing a planting date. Although the program is for annually planted forage, the RIAFP splits each year into two growing seasons with separate sign-up dates, which effectively divides winter forage and summer forage. Crops planted July 15 through December 15 are eligible for growing season 1, which has available rainfall index intervals from September through March. One widely used forage program that fits in growing season 1 is winter wheat and/or rye that is planted in the late summer or early fall and used for winter grazing. Growing season 2 provides coverage for crops planted December 15 through July 15 with available rainfall index intervals from March through September. Producers can double crop and receive indemnities for two growing seasons within the same year if they can prove they have double cropped for the past 2 years.
The growing season is the only choice made for CAT coverage. The coverage level is set by the RMA at 65% of the historical average rainfall level over the entire September–March interval, and the productivity factor is set at 45% of the county base acre value set by the RMA. The premiums for CAT coverage are fully subsidized by the USDA, though there is a $300 sign-up fee (USDA, FDIC, RMA, 2015).
Buy-up coverage offers the producer much more flexibility in designing a desired insurance product. Beyond the growing season, the producer next chooses the coverage level, which specifies the level of the rainfall index that would trigger payments. The expected rainfall index, which is calculated from historical data, is adjusted so that the baseline for each year is 100 (USDA, FDIC, RMA, 2013). Thus, the producer selects a coverage level ranging from 70% to 90% (USDA, FDIC, RMA, 2015). For example, if the producer chooses a 90% coverage level, an indemnity will be triggered if the actual rainfall index is less than 90.
Next, producers wishing to purchase buy-up coverage must choose the value per acre of their forage production. They accomplish this by choosing a productivity factor to adjust the producer's respective county base value that is provided by the RMA for each county within the participating states. This productivity factor can range from 60 to 150 in 1% increments where a choice of 100 would indicate that the producer believes the value of an acre of forage production is equal to the county base.
The final choice the producer must make is which rainfall indices to use in terms of months and the percent of value to allocate to these indices. The rainfall index is calculated over a period of 2 months with specific intervals available for each growing season. Each 2-month interval between September and March is available for growing season 1, whereas intervals within March to September are available in growing season 2 (USDA, FDIC, RMA, 2013). Producers must select three intervals within the time period for their respective growing seasons and can weight each intervalFootnote 1 up to 40% so that the intervals producers believe are more important have a larger impact on potential indemnity payments.
The choices discussed previously are factors in determining the cost of the producer's premium, the value of a potential indemnity payoff, and the value of the subsidy that the producer receives (USDA, FDIC, RMA, 2013). Subsidies are applied as a percent of premium cost and vary by the level of coverage the producer selects. The subsidy levels are set by the annual commodity report for the program (USDA, RMA, 2015a). The 2015 subsidy levels are 59% for 70% and 75% coverage levels, 55% for 80% and 85% coverage levels, and 51% for a 90% coverage level. Thus, the producer also chooses the percent of the premium that will be paid by the RMA when choosing a coverage level. For example, if the actuarially fair premium total cost is $2.16 for $21.60 of coverage per acre ($20 county base multiplied by 120% productivity factor multiplied by a 90% coverage level), the FCIC pays a 51% subsidy so that the producer only pays $1.06 per acre for the insurance (USDA, FDIC, RMA, 2013). In general, higher productivity factors and coverage levels lead to higher premiums, higher potential indemnity payoffs, and lower subsidy levels in terms of percent of premiums. If the goal is to maximize the amount of total subsidy in dollars, a producer should sign up for CAT coverage and also buy-up coverage at the 90% coverage level and with a 150% productivity factor (if planted for grazing, then only buy-up coverage is allowed).
Similar to other crop insurance programs, the FCIC sets limits pertaining to the maximum subsidy level and the maximum available funds for the program. The maximum subsidy possible is 60% of the premium amount for buy-up coverage, whereas CAT coverage is fully subsidized. The maximum annual amount allocated to this program from the FCIC fund is $12.5 million for fiscal years 2015–2018 (Shields, Reference Shields2014). Policies can be sold by approved insurance providers, but the policies cannot be similar to privately available hail insurance (Shields, Reference Shields2014).
2. Conceptual Framework
The general choice that a forage producer faces when crop insurance is available is similar to that of other insurance programs where the producer chooses the coverage level and an indemnity payment is triggered if production falls below a certain “threshold” level. However, the rainfall index values are used to replace the production levels. As most forage production operations are only one piece of a larger agricultural operation, the choice is one of many within a whole-farm optimization problem. We assume weak separability between a farm's forage production practices and other possible operations within the farm so that we may analyze forage production individually. Following Coble et al. (Reference Coble, Knight, Pope and Williams1996), we assume the producer will maximize the expected utility of wealth when considering the option of participation in the crop insurance program. Along with the discrete insurance participation choice, the producer also chooses the preferred coverage level and productivity factor. The coverage-level choice dictates the percentage of the rainfall index that will trigger an indemnity payment. A higher coverage level will result in a higher premium. The productivity factor choice is simply an adjustment to the county base production value per acre. The range of possible productivity factors is 60 to 150. Assuming the producer has chosen to plant forage that is insurable by the RIAFP, the risk-averse producer's expected utility objective function is written as
 $$\begin{equation}
\mathop {{\rm{max}}}\limits_{$$\begin{array}{*{20}{c}} {\scriptstyle A \in \left\{ {0,1} \right\}}\\ {\scriptstyle 70 \le \delta \le 90}\\ {\scriptstyle 60 \le \varphi \le 150} \end{array}$$} EU\left( \pi \right) = \int\!\!\!\int U\left( \pi \right)f\left( \Theta \right)dIdY,
\end{equation}$$
$$\begin{equation}
\mathop {{\rm{max}}}\limits_{$$\begin{array}{*{20}{c}} {\scriptstyle A \in \left\{ {0,1} \right\}}\\ {\scriptstyle 70 \le \delta \le 90}\\ {\scriptstyle 60 \le \varphi \le 150} \end{array}$$} EU\left( \pi \right) = \int\!\!\!\int U\left( \pi \right)f\left( \Theta \right)dIdY,
\end{equation}$$where the arguments are defined with the following equality constraints:
and where A is a discrete choice variable that equals 1 if the producer purchases crop insurance and 0 if not; δ denotes the threshold coverage-level choice ranging from 70% to 90%; φ is the productivity factor adjustment choice; EU(π) is the expected utility of profit; I is the actual index value and will trigger an indemnity payment if lower than the chosen threshold level of δ; P is the price for each unit of yield; k is the value of the indemnity payment per acre and is calculated as the product of the county base value per acre (B), the chosen coverage level, and the productivity factor; c is the cost of the insurance premium, and s is the value of the subsidy in dollars (both c and s vary with the coverage-level choice); r is a vector of other input costs; z is a vector of other inputs; f(Θ) represents the joint density of the index value and yield; and U'(π) > 0 and U ''(π) < 0 are the first and second derivatives of the utility function and are bounded such that the producer is defined as risk averse.
Note that in equation (1) an indemnity is triggered only if the rainfall index falls below the chosen coverage level and not if it simply falls below the historical average. Further, the indemnity payment varies based on the coverage-level and productivity factor choices. If purchasing buy-up coverage, the producer may choose and assign weights to the rainfall index intervals. Thus, the previously described model would be applicable to each interval that the producer chooses and would be adjusted by the weight the producer assigns to that interval.
Because we are interested in the relationship between yields, actual rainfall, and the rainfall index used in the RIAFP, we are specifically interested in the relationships of their distributions. The joint distribution of Θ represents the interaction between the rainfall index and forage yield. Also, nested within this distribution is the interaction of actual rainfall with the rainfall index and yield. This joint distribution is the area of focus for this article as we are interested in the relationships between the rainfall index, forage yield, and actual rainfall. Basis risk is reflected in f(Θ) because it reflects how closely the index correlates with yield. Basis risk could occur if the index does not perfectly identify the actual level of rainfall or if the index does not perfectly predict yields. In the case of extreme basis risk, I and Y would be independent, and the insurance program would not reduce risk but could still be beneficial to producers if subsidized enough.
3. Data
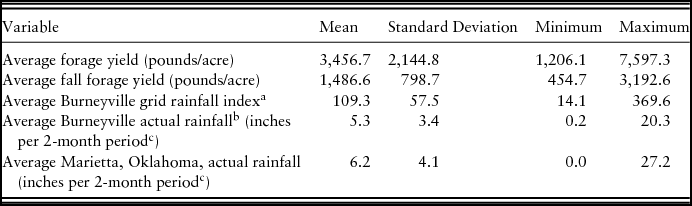
The data are from a long-term study of annually established cereal rye-ryegrass forage production at the Samuel Roberts Noble Foundation's Red River Farm located near the community of Burneyville in south-central Oklahoma from 1974 until the experiment was discontinued in 2008. The soil is a fine sandy loam. A small amount of wheat was also included in early years but was discontinued in 1994. This relatively long series of continuous agronomic data allows many years from which to consider the effectiveness of the design of the RIAFP. This experiment was initially used to evaluate the effect of the nitrogen fertilization rate and harvest timing on annual forage production but has since been used to analyze various lime and nitrogen application questions (i.e., Altom et al., Reference Altom, Rogers, Raun, Johnson and Taylor1996, Reference Altom, Rogers, Raun and Thomason2002; Tumusiime et al., Reference Tumusiime, Brorsen, Mosali and Biermacher2011a, Reference Tumusiime, Brorsen, Mosali, Johnson, Locke and Biermacher2011b). This expansive data set includes actual forage clippings in pounds, lime and fertilizer treatments, and planting and clipping dates over 33 years for a total of 3,845 plots. Plots differed by varying treatments of fertilizer and lime. Forage yields were determined by clipping each 12-by-13-foot plot multiple times per year to simulate grazing. Forage yield is split between clipping seasons. As most plots in the data were planted in September, fall forage yield is calculated as the sum of clippings from the planting date up to March 1. Clippings that occurred between March 1 and the final clipping of the year (usually near the end of May) are considered spring forage. The annual forage yield for each plot is the sum of fall and spring forage yields. Descriptive statistics for these data are provided in Table 1.
Table 1. Descriptive Statistics for Burneyville, Oklahoma, Forage Trials for 1974–2008

a We present the average value across all index intervals from September to May.
b N = 16 for this variable because data were only available from 1993 to 2008.
c Because the rainfall index is only available over 2-month intervals, we present the actual rainfall data in a consistent manner. Therefore, the mean for this variable is the average cumulative rainfall across each 2-month period from September to May.
Note: N = 33.
These data are especially applicable in evaluating the RIAFP because they are collected from an experiment representative of many forage programs that would qualify for the RIAFP. The forage program used would fit into growing season 1 of the RIAFP and is similar to the practices of many producers who annually plant winter forage for grazing. Such producers are primary candidates for participation in the RIAFP.
We are ultimately interested in how closely the yields each year follow the RMA rainfall index used to trigger indemnity payoffs in the RIAFP. Therefore, to calculate a single yield observation for each year or season, we must first determine which observations should be used because the data include yields from plots with different fertilizer and lime treatments. Because the effects of fertilizer treatments are not the focus of this article, we use only the yields from plots with nitrogen application of 100 pounds/acre, which is consistent with the Samuel Roberts Noble Foundation recommendation and results from previous work using data from the Red River Farm (Tumusiime et al., Reference Tumusiime, Brorsen, Mosali, Johnson, Locke and Biermacher2011b). Further, for years 1980 to 2008, we use only plots with lime treatments. Prior to 1980, none of the plots were treated with lime because no lime was needed. We account for fall and spring clippings by treating a year as a crop year. All plots were initially planted in September or early October and clipped for the last time within 1 month of the first week of May. To achieve a single yield observation for each plot for each season each year, we simply sum the yields from each clipping.
We treat the sum of fall clippings as the growing-season-1 forage yield defined by the RIAFP. The criteria to which plots must adhere are the same as for the average annual forage yield, except that the 100 pounds/acre of nitrogen must be applied during the fall season instead of across fall and spring seasons. Therefore, the growing-season-1 forage yield is defined as the average sum of fall clippings for each year.
Rainfall index data for the grid in which the farm is located are collected from the USDA RMA's decision tool (AgForce [AF], Grazing Management Systems [GMS], and RMA, 2014). Further, actual rainfall data are available from two sources: a Mesonet weather data collection station located at the Red River Farm for years 1993 to 2008 and a National Climatic Data Center (NCDC) weather data collection station in nearby Marietta, Oklahoma, for 1974 to 2008 (Mesonet, 2014; NCDC, NOAA, 2014a). The distance between Marietta, Oklahoma, and the Samuel Roberts Noble Foundation Red River Farm in Burneyville, Oklahoma, is approximately 6 miles. Because the rainfall index is calculated using the total precipitation over 2-month periods, we create matching periods using the actual rainfall data by summing the rainfall in the respective months of each period. Because all of the plots in our data were planted during growing season 1 as specified by the provisions of the RIAFP, only the 2-month intervals within September to March can be selected for buy-up coverage (USDA, FDIC, RMA, 2013). Thus, we are left with six growing-season-1 rainfall intervals. Intervals outside of those allowed in growing season 1 are used when analyzing annual forage yield because some of the clippings occurred in months later than those for which the RIAFP provides rainfall index intervals.
The rainfall index is calculated from data collected by undisclosed NOAA weather stations from 1948 to 2008 (RMA, Kansas City, MO, unpublished data, “2010 and Beyond Rainfall Index Processing”). The RMA does not disclose which stations are used in the rainfall index calculation to prevent producers from tracking these stations to predict whether an indemnity will be paid (RMA, Kansas City, MO, personal communication). Although we cannot know exactly which stations are used, we do know that NOAA used only stations that reported at least 75% of the time from 1948 to 2010, and thus the Burneyville station is not used. From these data, interpolation is used to create 0.25° latitude by 0.25° longitude grids (approximately 12 by 12 miles in Oklahoma) using a modified inverse distance weighting technique based on Cressman's (Reference Cressman1959) methods (RMA, Kansas City, MO, unpublished data, “2010 and Beyond Rainfall Index Processing”).Footnote 2 Four weather stations are used daily to calculate precipitation, and the weight of each station is determined by its distance from the grid. These four stations can change daily depending on how often they report (RMA, Kansas City, MO, personal communication). The closest reporting weather station has the greatest impact on each specific daily average.
A key issue in creating an index for precipitation using weighted averages of nearby weather stations is the spatially variable nature of rainfall. Even within a 12-by-12-mile area, rainfall can be quite different depending on many weather factors. The RMA uses the ratio of the current precipitation and historical precipitation for each grid when calculating the rainfall index (RMA, Kansas City, MO, unpublished data, “2010 and Beyond Rainfall Index Processing”). Chen et al. (Reference Chen, Shi, Xie, Silva, Kousky, Higgins and Janowiak2008) find that using the ratio of current and historic precipitation allows for the interpolation method to better capture the spatial distribution of precipitation.
From these daily precipitation data, 2-month intervals are calculated by summing precipitation for the days within the interval. Thus, for growing season 1, six 2-month intervals of total precipitation are created beginning with the September–October interval. Then, the rainfall index is calculated for each specific interval using the deviation between that interval and a historical long-term average rainfall (RMA, Kansas City, MO, unpublished data, “2010 and Beyond Rainfall Index Processing”). The historical average is calculated using data from 1948 to 2 years prior to the interval of interest and is adjusted to reduce the likelihood of extreme weather events affecting the index value. The final rainfall index is calculated by dividing the current interval rainfall by the historical long-term average rainfall and multiplying by 100. A step-by-step process of this calculation as provided by the RMA (Kansas City, MO, unpublished data, “2010 and Beyond Rainfall Index Processing”) is shown in Appendix A.
Although we cannot be certain which stations were used in the calculation of the rainfall index because of the nondisclosure of the NOAA weather stations used, the Marietta rainfall weather station used as a measure of actual rainfall data is listed as a NOAA weather station (NCDC, NOAA, 2014b). It is possible that data from this station were used in the calculation of the rainfall index for the grid in which Burneyville lies. Fifteen stations are located within 50 miles of the Samuel Roberts Noble Foundation research farm in Burneyville that have reported weather data at least 75% of the time since 1948 (NCDC, NOAA, 2014b). The Marietta, Oklahoma, station is the closest (6 miles) and the Muenster, Texas, station is the next closest at approximately 17 miles.
4. Empirical Model
The key assumption of the RIAFP is that forage production is correlated with the rainfall indices, and therefore, a decrease in the index would result in a decrease in forage production. Thus, we are interested in the relationship of the yield and rainfall index variables within the joint distribution f(Θ) from equation (1).
With a single annual observation for yield, the data-generating process is specified as
where Yt represents average annual forage yields (pounds/acre) for each year t, where t = 1, . . ., 34, which corresponds with the years 1974–2008; R t is a vector of the rainfall index intervals provided by RMA; εt represents the experimental error terms, where εt ~ N(0, σ2ε); and β0 and β i are parameters to be estimated. Because we are essentially estimating a linear approximation under the assumption of normality, we are interested in the cross moments between the dependent variable and independent variable. Thus, we calculate the Pearson product-moment correlation specified as
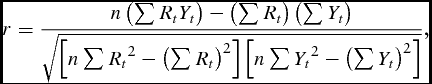 $$\begin{equation}
r = \frac{n\left( \sum {R_t}{Y_t} \right) - \left( \sum {R_t} \right)\left( \sum {Y_t} \right)}
{\sqrt {\left[ n \sum {R_t}^2 - \left( \sum {R_t} \right)^2 \right]\left[ n \sum {Y_t}^2 - \left( \sum {Y_t} \right)^2 \right]}},
\end{equation}$$
$$\begin{equation}
r = \frac{n\left( \sum {R_t}{Y_t} \right) - \left( \sum {R_t} \right)\left( \sum {Y_t} \right)}
{\sqrt {\left[ n \sum {R_t}^2 - \left( \sum {R_t} \right)^2 \right]\left[ n \sum {Y_t}^2 - \left( \sum {Y_t} \right)^2 \right]}},
\end{equation}$$where r is the Pearson product-moment correlation, and n is the number of observations to show this relationship. The relationship between forage yield and the rainfall index, as well as the relationship between the rainfall index and actual rainfall, is estimated using the same method.
Because the data do not fit perfectly into the design of the program for growing season 1, we separate the estimation into separate designs. To match the rainfall index intervals to the actual production process used, we estimate correlations between annual forage yield and the rainfall measures for each interval within the actual growing season, September to May. To test the design of the program using only those yields that fit within growing season 1, we estimate correlations between annual growing-season-1 forage yields and the rainfall measures for each interval within September to March.
Beyond correlations, we also adjust for planting date and a linear time trend using a linear regression model:
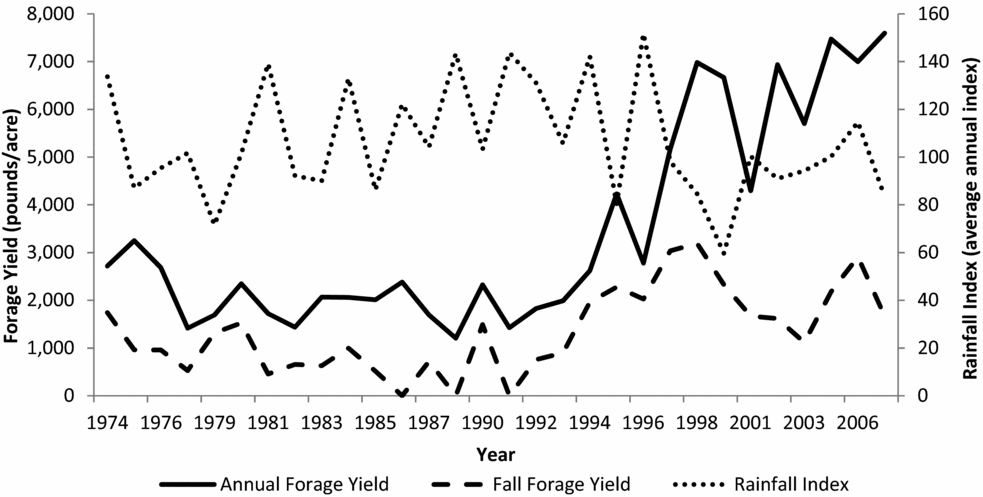
where t denotes time; D is the number of days between the planting date and September 1 of each year; α0, . . ., αi are the parameters to be estimated; and vt represents the experimental error terms, where vt ~ N(0, σ2v). Figure 1 indicates a likely structural change beginning around 1993 as forage yields increase after remaining relatively flat from 1974 to 1993. Thus, a Chow test for structural change is performed and indicates a significant structural break at year 1993 (Chow, Reference Chow1960). Therefore, the regression in equation (4) is estimated separately for the 1974–1992 and 1993–2008 time periods.

Figure 1. Average Spring Forage Yield in Relation to Average Annual Rainfall Index for the Grid in Which Burneyville, Oklahoma, Is Located
Because of the program design, at least three rainfall intervals must be chosen from the September to March period used for growing season 1. Because we have only 7 months and the intervals chosen cannot overlap, a producer can choose to leave out September, November, January, or March. To estimate just two models where all possible intervals are used at least once, we estimate linear models for two interval combinations: one in which September is the month left out and one in which March is the month left out.
5. Results
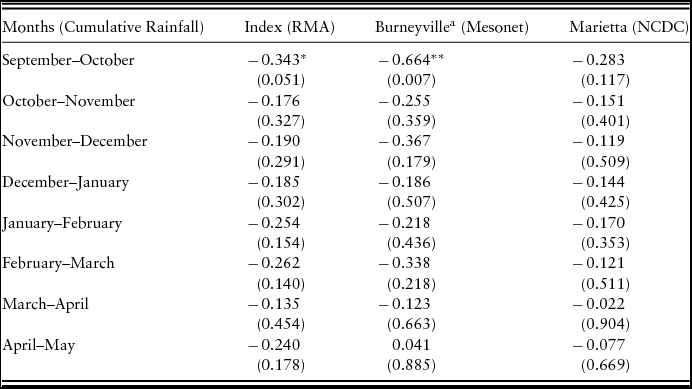
The estimated Pearson product-moment correlations between annual forage yield and the rainfall variables are provided in Table 2 for each interval within the actual growing season. The correlations show that rainfall and forage yield are weakly dependent at best and are, surprisingly, nearly all negative,Footnote 3 though only the September–October intervals for the rainfall index and actual rainfall in Burneyville are statistically significant at conventional levels. These results seem to follow a visual check of the data provided in Figure 1 as annual forage yield and the rainfall index do not appear to move together. The results for the full data series using the Marietta, Oklahoma, actual rainfall are comparable to the results using the Burneyville, Oklahoma, data.
Table 2. Pearson Correlations between Annual Forage Yield and Rainfall Variables for 1974–2008

a N = 15 for this variable as data were only available from 1993 to 2008.
Notes: N = 33. Probability >| r | in parentheses. Asterisks (***, **, and *) denote significance at the 1%, 5%, and 10% levels, respectively. NCDC, National Climatic Data Center; RMA, Risk Management Agency.
As a check for robustness, we consider the possibility that rainfall is more important in relatively dry years as opposed to years with average or above-average rainfall. We find similar insignificant correlations between rainfall and forage yield even in years of below-average rainfall.
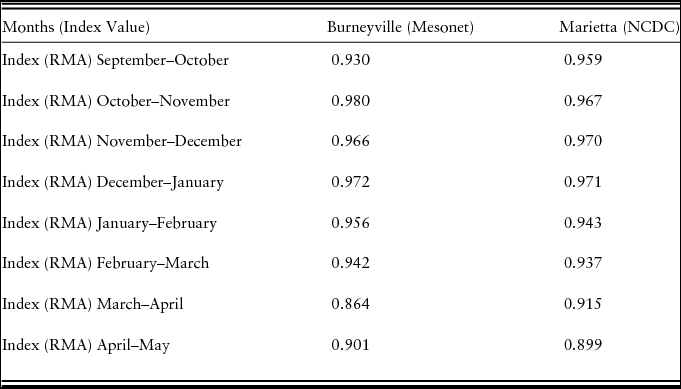
Of particular interest is the correlation between the rainfall index and actual rainfall at the site of the plots. Table 3 provides the correlations between the rainfall index and the actual rainfall variables. As shown, all of the intervals for the rainfall index have high positive correlations with each actual rainfall variable implying that the rainfall index performs very well as an indicator of actual rainfall, a key assumption of the RIAFP. We test this finding in other locations and always find the rainfall index to be highly positively correlated to local rainfall data and statistically significant.Footnote 4
Table 3. Pearson Correlations between Burneyville, Oklahoma, Rainfall Index Intervals and Actual Rainfall Intervals for 1974–2008

Notes: N = 33. All correlations are statistically significant at the 1% level. NCDC, National Climatic Data Center; RMA, Risk Management Agency.
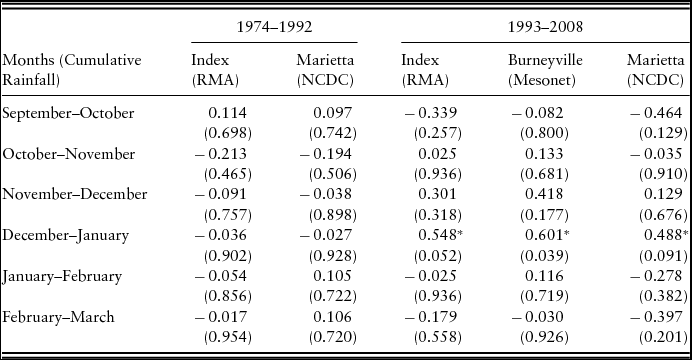
To test how well the program works with data that fit the specific intervals available in growing season 1, Table 4 presents the correlations between the forage yield in growing season 1 and the rainfall variables. The correlations are split into separate time frames to account for the apparent structural change beginning in 1993. The correlations for the 1974–1992 time period are low and often negative, although none are statistically significant. For the 1993–2008 time period, the intervals between October and February all have the expected positive sign for the correlation between yield and actual rainfall in Burneyville. Further, the correlations for the December–January interval are positive and statistically significant at conventional levels for all of the rainfall variables.
Table 4. Pearson Correlations between Growing-Season-1 Forage Yield and Rainfall Variables for 1974–1992 and 1993–2008

Notes: Probability >| r | in parentheses. Asterisks (***, **, and *) denote significance at the 1%, 5%, and 10% levels, respectively. NCDC, National Climatic Data Center; RMA, Risk Management Agency.
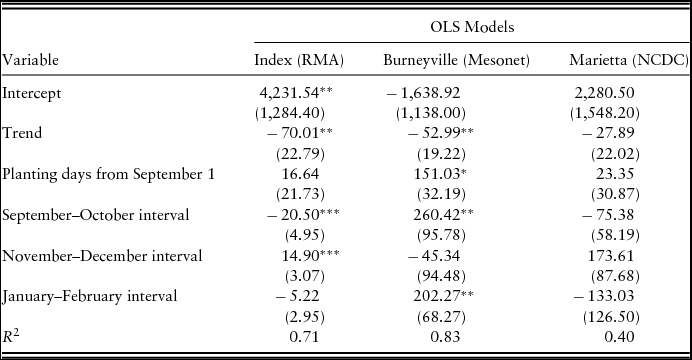
Tables 5 and 6 report linear regression coefficients for the effects of planting date, year, and the rainfall variables on growing-season-1 forage yield. Durbin-Watson autocorrelation tests found that autocorrelation was an issue for each model. Therefore, the Newey-West autocorrelation consistent covariance estimator is used, and the standard errors reported are Newey-West standard errors (Greene, Reference Greene2012). As shown in the model using the Burneyville actual rainfall intervals, each additional day waited to plant from September 1 increases growing-season-1 forage yield by 71 to 151 pounds depending on the intervals, which indicates that the forage was often planted too early in our data set. The January–February interval is positive and statistically significant in the Burneyville actual rainfall model implying that a 1-inch increase in the cumulative rainfall during January and February leads to a 202.27-pound increase in growing-season-1 forage yield. Differing from the estimated correlation in Table 4, the coefficient for the September–October interval is positive and statistically significant. The October–November and December–January intervals are also positive and statistically significant at conventional levels.
Table 5. Ordinary Least Squares Coefficients for Rainfall Intervals’ Effect on Growing-Season-1 Forage Yield for 1993–2008 Beginning with September–October Interval

Notes: Newey-West autocorrelation consistent standard errors in parentheses. Asterisks (***, **, and *) denote significance at the 1%, 5%, and 10% levels, respectively. NCDC, National Climatic Data Center; RMA, Risk Management Agency.
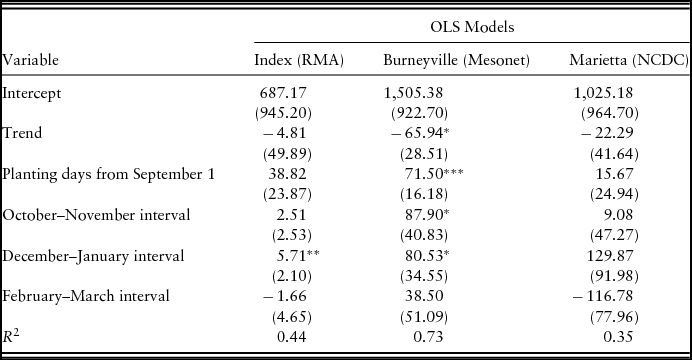
Table 6. Ordinary Least Squares Coefficients for Rainfall Intervals’ Effect on Growing-Season-1 Forage Yield for 1993–2008 Beginning with October–November Interval

Notes: Newey-West autocorrelation consistent standard errors in parentheses. Asterisks (***, **, and *) denote significance at the 1%, 5%, and 10% levels, respectively. NCDC, National Climatic Data Center; RMA, Risk Management Agency.
For the rainfall index models, the November–December interval is positive and statistically significant. The estimate implies that a one-unit (or percent) increase in the rainfall index leads to a 14.9-pound increase in the growing-season-1 forage yield. The December–January interval is also positive and statistically significant. The September–October interval is negative and statistically significant. Although only 6 miles away from the location of the plots where the data were collected, none of the estimates in the Marietta, Oklahoma, actual rainfall model are statistically significant, and these two models also are the poorest at explaining the variation in the growing-season-1 forage yield as shown by the R 2 values. The Marietta model including the September–October interval explains only 40% of the variation in forage yield, whereas the Burneyville model for the same intervals explains 83% of the variation in yield.
The mostly insignificant correlations between forage yield and rainfall lead to questions about whether there are other variables that might outperform rainfall in explaining forage yield. Though not included in the RIAFP, we consider preseason rainfall and air temperature as possible explanatory variables. However, neither of these variables is significantly correlated with forage yield, and they are not statistically significant in the linear regressions. Thus, these results were omitted from the model and results to ensure parsimony.
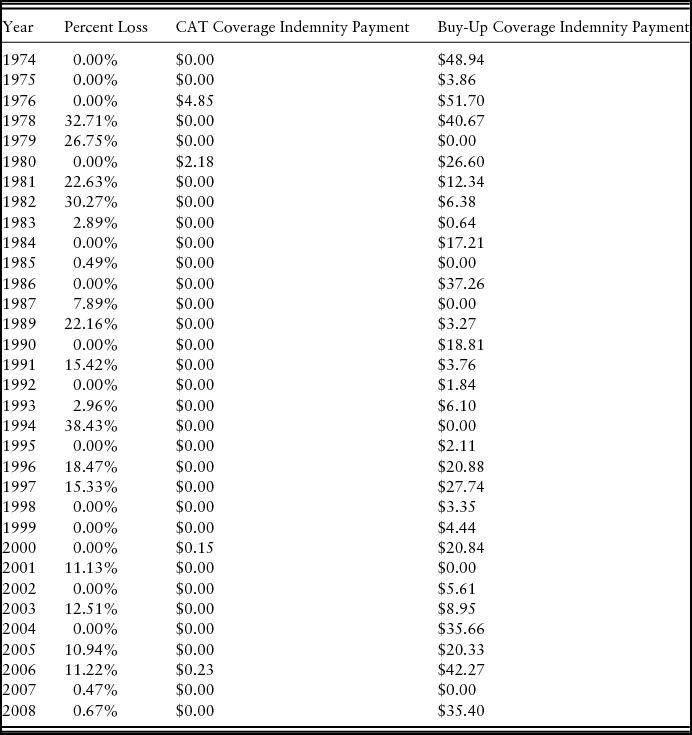
Because the premiums are actuarially fair and heavily subsidized, a risk-neutral producer should sign up for the maximum level of coverage in order to maximize the total amount of the subsidy. Table 7 provides the annual indemnity payments coinciding with our data if the RIAFP had been available and the acreage was enrolled at a 90% coverage level and 150% productivity factor (the levels that maximize the total subsidy). Yield loss is calculated as the percent loss of actual forage yield relative to the predicted forage yield from the rainfall index linear regression reported in Table 5. The rainfall index model is used because we do not have actual rainfall data for 1974–1993, and the model is separated at 1993 to account for the apparent structural change shown in Figure 1. The indemnity payments per acre are calculated using the methodology for calculating indemnity payments as detailed by USDA, FDIC, RMA (2013). These values are what the actual CAT and buy-up payouts would have been if the RIAFP had been available each year and are used to illustrate the relationship between yield loss and indemnity payments. As shown in Table 7, the CAT payouts do not occur in years of relatively low yield. Likewise, the indemnity payouts from the buy-up coverage do not seem to be linked to the percent of yield loss.Footnote 5 These results support the findings from the empirical model of no correlation between the rainfall index and forage yield.
Table 7. Annual Yield Loss Percent and Indemnity Payment per Acre

Notes: Yield loss percent is calculated as the actual level of forage production relative to predicted level of forage yield using the rainfall index linear regression represented in Table 5. Buy-up coverage payments assume 90% coverage level and 150% productivity factor. CAT, catastrophic risk.
For a producer in Burneyville, Oklahoma, the RIAFP would have triggered an indemnity payment under CAT coverage for 5 years from 1974 to 2014, or approximately 13% of the time, for a total payoff of $14.67 and a total premium subsidy of $31.98 per acre. The number of payoffs increases to 32 out of the 40 years for buy-up coverage at a 90% coverage level if the intervals chosen are October–November, December–January, and February–March. These intervals are chosen because the December–January interval, which we find to have the most significant correlation with forage yield, is included. Using the 90% coverage level and the 150% productivity factor, which maximizes the total subsidy dollars, a producer would have paid $461 in premiums with payoffs totaling $661 per acre. Out of the 40 years analyzed, the annual payoff would have exceeded the producer's portion of the premium 20 times. For this scenario, the total subsidy paid as 51%Footnote 6 of the total premiums would have been $480.09.
In total, a producer in Burneyville, Oklahoma, from 1974 to 2014 would have gained an extra $200 per acre by participating in the RIAFP at the highest levels of buy-up coverage allowed. Without the subsidies for buy-up coverage, the insurance would not have been profitable as producers would have paid $280 more in premiums than they would have earned in payoffs per acre. It is important to note that we do not have the actual premiums charged from 1974–2013 as the RIAFP was not yet established. Thus, we use the 2015 premiums in the retrospective analysis, which are very similar to the 2014 premiums.
6. Conclusions
We find that the rainfall index is well designed because it has high positive correlation with actual rainfall. Thus, the program design should work well at insuring against a particularly dry year, which is a key purpose of the RIAFP. However, the rainfall index would have done little to provide yield risk protection for our specific data. When considering only the yields within growing season 1 as defined by the RIAFP, we find one example of the expected positive correlation between the December–January rainfall index and forage yield. The other correlations were either negative or statistically insignificant.
Although the RIAFP does well at insuring against a particularly dry year, it does little toward protecting producers against lost forage yields. We find that the lack of correlation between forage yield and the rainfall index does not depend on whether it is a wet or dry year. Further, the indemnity payments do not seem to follow the level of yield loss across the time period in our data.
Although including all of the index intervals in which the forage was actually harvested does not provide any additional yield risk protection for our data, the program would benefit from allowing producers to select intervals for any months prior to when they expect to harvest. Currently, the RIAFP limits the intervals producers may select depending on when the crop is planted. Many cool-season forages such as ryegrass and winter wheat are planted in early fall and harvested in months later than ones for which the RIAFP provides index intervals. Rainfall index intervals containing the late spring months for forage planted in growing season 1 would more closely match the time of production, but production in these late spring months was also not closely correlated with rainfall.
The program offers clear benefits to annual forage producers. Because of the high subsidy levels, eligible expected profit–maximizing producers should sign up for buy-up coverage at the maximum levels allowed as long as this does not affect their eligibility for other programs. The intervals selected do not make much difference, but the December–January interval is statistically significant and positively correlated with yield, so we suggest assigning it with the maximum weight allowed.
These results are from a single location and may not necessarily extrapolate to other forages, soil types, or weather patterns. Similar consideration of other scenarios cannot be performed because long-term forage yield data are not available across the many possible combinations of variables. Perhaps rainfall would be more of a constraining input in drier areas further west and the correlations between forage yield and the rainfall index would be stronger.
A key issue of any index insurance product is determining the basis risk resulting from the inability to perfectly predict yields. This occurs in the RIAFP as the rainfall index is not a good predictor of forage yields in our data. As a result, although the RIAFP is beneficial to producers because of the high subsidy levels, participating producers should not expect it to perform well at reducing yield loss risk. The lack of correlation between forage yield and the rainfall index exposes a significant weakness of the RIAFP as it would not provide the intended risk protection.
One of the contentious points in the recent farm bill debate was equity, both in terms of regional equity and in terms of providing subsidies to producers of nonprogram crops such as annual forage (Freshwater, Reference Freshwater2015). Freshwater (Reference Freshwater2015) argues that farm programs are simply a way to provide equity by transferring federal dollars to rural areas, and thus, a farm program should be viewed not from an efficiency standpoint, but by how well it transfers federal dollars to underserved areas. Although the program seems to provide drought risk but do little to reduce yield loss risk, the RIAFP can still meet what is a key goal—to transfer income to annual forage producers.
The implications for producers are clear; because the program does little to reduce yield loss risk, they should sign up for buy-up coverage at the maximum levels allowed. If a producer declines the buy-up coverage, then he or she should sign up for the fully subsidized CAT coverage. Had the RIAFP been available, signing up for buy-up coverage at the maximum levels would have led to a $200 increase per acre in total producer profit over the past 40 years. Without the subsidy, the same coverage would have led to a $280 decrease per acre in producer profit. Thus, the RIAFP provides producers with higher expected returns than would be expected without the subsidized insurance.
Over the time period for our data, total payouts would have been less than the unsubsidized premiums. Although the method the RMA uses to calculate the premiums is proprietary information, over the 1949–2014 period for which the RMA has rainfall data to calculate premiums, the payouts and the premiums are much closer. The drought years of the 1950s may have had a strong influence on the premium calculation.
Appendix A
The following is a step-by-step calculation of rainfall index as provided by the U.S. Department of Agriculture, Risk Management Agency (Kansas City, MO, unpublished data, “2010 and Beyond Rainfall Index Processing”):
1. The system first counts the number of sample values in the historical period (1948 to 2 years prior to the year and interval of interest). For example, if 2009 is the year for which rainfall index is being calculated, then the historical period for calculating the long-term average is January 1, 1948–December 31, 2007. The count is used as the sample size for long-term average calculations.
2. The system then conducts the capping by assessing how many samples are outliers or outside of the typical range of rainfall values. For the analysis, 99.99% of all values are considered typical rainfall values; the remaining 0.01% of values are considered outliers. For this calculation, the sample size determined in step 1 is multiplied by 0.0001, and the result is rounded to a whole value. The result is the number of outliers that will be removed from the index calculation. For example, if the result is three outliers, then the third-highest value becomes the cap value. Therefore, all rainfall events that are greater than the cap value become the cap value. This analysis is conducted for each individual grid in the National Oceanic and Atmospheric Administration data.
3. The system then calculates the historical average for each interval. Intervals start each month and continue for a span of 2 months (e.g., interval 1 contains the months of January and February, interval 2 is February to March, and so on until every month is represented). There are 11 intervals per year. For each target grid, the rainfall is accumulated (summed) for all days in the interval, and then a long-term average is calculated by averaging the accumulated rainfall across years. The result becomes the historical average for the interval of interest. As with step 2, the historic index is calculated for each grid in the database.
4. Rainfall for the current interval of interest is accumulated for the interval period for the target grid. This becomes the current interval rainfall.
5. Finally, the rainfall index is calculated as follows:
 $$\begin{equation}
{\text{Rainfall Index}} = \frac{{{\text{Current Interval Rainfall}}}}{{{\text{Long}} - {\text{Term Average Rainfall}}}} \times 100.
\end{equation}$$
$$\begin{equation}
{\text{Rainfall Index}} = \frac{{{\text{Current Interval Rainfall}}}}{{{\text{Long}} - {\text{Term Average Rainfall}}}} \times 100.
\end{equation}$$