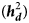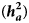Introduction
Sheep were the first farm animals domesticated by humans about 8–10 thousand years ago. The small size, the ability to be domesticated and the high performance for meat, milk and wool production were the reasons to domesticate sheep. Aryans were the first people which domesticate sheep. Studies show that sheep were domesticated in the land that is now called Kurdistan, and most of the domestic sheep in the world originated from wild flocks of sheep scattered in this area. Therefore, Iran can be considered as the primary land of sheep breeding (Deng et al., Reference Deng, Xie, Wang, Zhao, Lv, Li, Yang, Yu, Shen and Gao2020). Baluchi is a domesticated breed of sheep originating from southwest Pakistan, eastern Iran and southern Afghanistan. This breed comprises 12% of the total sheep population in Iran and because of its large population, has a significant contribution to the total meat and mutton production. The animals of this breed are known with small size, fat tail, carpet wool and white colour. They are good foragers and adapted to a wide range of harsh environmental conditions in the north-eastern parts of Iran which known as North-, South- and Razavi-Khorasan provinces (Bahreini-Behzadi et al., Reference Bahreini-Behzadi, Aslaminejad, Sharifi and Simianer2014).
In Iran, during recent decades, we have witnessed an increasing demand for lamb and mutton mainly because of population growth. Due to the fact that the supply of meat from sheep does not cover the demand, breeding schemes have been conducted to increase sheep production. Since there are limitations on increasing sheep population, efforts have been focused on increasing performance per head. However, most selection programmes have focused on growth and reproductive traits, ignoring traits related to efficiency of feed utilization. In the intensive systems that are expanding in Iran, in addition to growth and reproduction traits, traits related to feed efficiency are of great importance, because in these systems, the cost of feed is a significant part of the production system, up to 60%. Therefore, any improvement in efficiency of feed utilization will lead to higher profitability of the production system (Ghafouri-Kesbi and Gholizadeh, Reference Ghafouri-Kesbi and Gholizadeh2017). To improve feed efficiency, selection based on traits such as Kleiber ratio (KR) (Kleiber, Reference Kleiber1947), efficiency of growth (EF) (Dass et al., Reference Dass, Sing and Ayub2004) and relative growth rate (RGR) (Fitzhugh and Taylor, Reference Fitzhugh and Taylor1971), as indirect indicators of efficiency of feed utilization, have been suggested. KR, EF and RGR are useful measurements to identify animals which have lower maintenance requirements.
The narrow-sense heritability of a trait (h2), defined as the proportion of the phenotypic variance accounted for by the additive genetic effects, is an important indicator of the extent to which a trait can be improved by selection. Information on heritability is crucial in the formulation of optimum breeding objectives and an effective genetic improvement programme. So far, for estimating heritability of economic traits in sheep efforts have mainly focused on estimating direct and maternal additive genetic variance, ignoring additional components such as dominance effects (Sing et al., Reference Singh, Pannu, Narula, Chopra, Naharwara and Bhakar2016; Ghafouri-Kesbi and Gholizadeh, Reference Ghafouri-Kesbi and Gholizadeh2017; Javanrouh et al., Reference Javanrouh, Baneh and Ghafouri-Kesbi2021). The results of recently published articles show that the dominance genetic effects significantly contribute to the phenotypic variation of production and reproduction traits of domestic animals in a range between 1 and 25% (Jasouri et al., Reference Jasouri, Zamani and Alijani2017; Ebrahimi et al., Reference Ebrahimi, Dashab, Faraji-Arough and Rokouei2019; Sadeghi et al., Reference Sadeghi, Rokouei, Valleh, Abbasi and Faraji-Arough2020, Reference Sadeghi, Rokouei and Faraji-Arough2021). Including the dominance genetic effects in the genetic evaluation model can (1) lead to a better understanding of the genetic architecture of traits, (2) increase the accuracy of genetic evaluation, and (3) improve the efficiency of breeding programmes via determining the relative importance of dominance genetic effects (Varona et al., Reference Varona, Legarra, Toro and Vitezica2018). Therefore, it would be reasonable to include dominance genetic effect in models for genetic evaluation of economic traits in sheep. Although genetic parameters for growth- and efficiency-related traits of Baluchi sheep have been estimated by Ghafouri-Kesbi and Gholizadeh (Reference Ghafouri-Kesbi and Gholizadeh2017), no attempt has been made to quantify relative contribution of dominance genetic effects to phenotypic variation of efficiency-related traits in this breed. Therefore, this study was conducted to estimate dominance genetic effects on Kleiber ratio, efficiency of growth and relative growth rate in Baluchi sheep.
Material and methods
Data
The data used in the present study were retained from Abbasabad Baluchi Sheep breeding station (flock 1), Mashhad, Khorasan Razavi, Iran. This experimental population of Baluchi sheep was founded in early 1960s. In general, the flock is reared by following conventional industrial procedures. The mating period commenced in August and September and lasted for 51 days. Lambing took place from beginning of February to the end of March. At birth, the relevant information about newborn such as sex, birth type, birth date, birth weight, sir ID and dam ID were recorded. In addition, body weights were recorded at monthly intervals starting from birth until 4 months of age. Body weights for 6, 9 and 12 months of age were also recorded. Lambs were weaned on average age of 90 days. They were raised separately from older animals until one year of age. During this period, they were not subjected to any form of culling unless they were physically unsound. Animals are kept indoors during winter and received a ration consisted of wheat and barley straw, alfalfa hay, sugar beet pulp and concentrate. According to the requirement, the food of the ewes was supplemented with concentrates during pregnancy and the nursing period. To protect animals from various diseases, vaccinations were performed twice a year. The sheep were dewormed with drugs and dipped in anti-parasite bath twice a year.
Traits
Raw data included birth weight (BW) and weaning weight (WW). Weaning weights were adjusted for 90 days of age. Pre-weaning average daily gain (ADG) was calculated as total gain divided by the number of days in the period. The estimates of ADG was then used to calculate corresponding Kleiber ratios as KR = ADG/WW0.75. Body weights were used to calculate efficiency of growth as EF = [(WW–BW)/BW] × 100. Relative growth rate from birth to weaning (RGR) was calculated as: RGR = [Loge(WW)–Loge(BW)]/90.
Statistical analysis
To identify fixed effects for each trait, GLM procedure of SAS (2004) was fitted to the data. Fixed effects included birth year, lambing age of dam, lamb sex and birth type. These fixed effects were significant (P < 0.05) for all traits and were subsequently included in the linear mixed models. To estimate (co)variance components and genetic parameters, the WOMBAT programme (Meyer, Reference Meyer2020) was used. Each trait was analysed with 12 univariate animal models, including various combinations of additive genetic, dominance genetic, maternal additive genetic and maternal permanent environmental effects (Table 1). As the simplest model, model 1 included only random animal effects, and model 12 which was the most complete animal model, included additive genetic, dominance genetic, maternal additive genetic, maternal permanent environmental and covariance between direct and maternal additive genetic effects. The general representation of the model 12 was as follows:
where y is the vector of observations. β is the vector of fixed effects fitted with design matrix X. Z1, Z2, Z3, and Z4 are incidence matrices relating observations to additive genetic, dominance genetic, maternal permanent environmental and maternal additive genetic, respectively. The (co)variance matrix for the random effects was as follows:

where a, d, c, m and e are vectors for additive genetic, dominance genetic, maternal permanent environmental, maternal additive genetic and residual effects, respectively. $\sigma _{\rm a}^2 , \;\;\sigma _{\rm d}^2 , \;\;\sigma _{\rm c}^2 , \;\;\sigma _{\rm m}^2$![]() and ${\rm \sigma }_{\rm e}^2$
and ${\rm \sigma }_{\rm e}^2$![]() are additive genetic variance, dominance genetic variance, maternal permanent environmental variance, maternal additive genetic variance and residual variance, respectively. A and D are the additive and dominance numerator relationship matrix, respectively. Ic and Ie are identity matrices of appropriate dimensions. The matrix D and its inverse were constructed using nadive package (Wolak, Reference Wolak2022) in R (R Development Core, 2023) and then fitted by GIN option in WOMBAT (Meyer, Reference Meyer2020). The information criterion of Akaike (AIC) (Reference Akaike1974) was computed to rank the models according to their power to fit the data. Let p denotes the number of random (co)variance parameters to be estimated, and Log L is the maximum likelihood, then the information criterion is defined as AIC = −2 Log L + 2p. The model yielding the smallest AIC fits the data best.
are additive genetic variance, dominance genetic variance, maternal permanent environmental variance, maternal additive genetic variance and residual variance, respectively. A and D are the additive and dominance numerator relationship matrix, respectively. Ic and Ie are identity matrices of appropriate dimensions. The matrix D and its inverse were constructed using nadive package (Wolak, Reference Wolak2022) in R (R Development Core, 2023) and then fitted by GIN option in WOMBAT (Meyer, Reference Meyer2020). The information criterion of Akaike (AIC) (Reference Akaike1974) was computed to rank the models according to their power to fit the data. Let p denotes the number of random (co)variance parameters to be estimated, and Log L is the maximum likelihood, then the information criterion is defined as AIC = −2 Log L + 2p. The model yielding the smallest AIC fits the data best.
Table 1. The random (co)variance components fitted in the 12 models to efficiency-related traits in Baluchi sheep
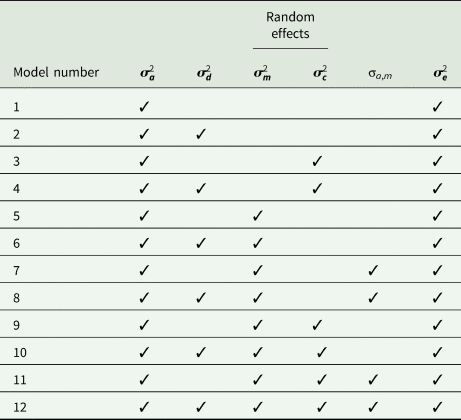
${\boldsymbol \sigma }_{\boldsymbol a}^2$![]() , additive genetic variance; ${\boldsymbol \;\sigma }_{\boldsymbol d}^2$
, additive genetic variance; ${\boldsymbol \;\sigma }_{\boldsymbol d}^2$![]() , dominance genetic variance; ${\boldsymbol \sigma }_{\boldsymbol c}^2$
, dominance genetic variance; ${\boldsymbol \sigma }_{\boldsymbol c}^2$![]() , maternal permanent environmental variance; ${\boldsymbol \;\sigma }_{\boldsymbol m}^2$
, maternal permanent environmental variance; ${\boldsymbol \;\sigma }_{\boldsymbol m}^2$![]() , maternal additive genetic variance; σa,m, direct-maternal additive genetic co-variance; ${\boldsymbol \sigma }_{\boldsymbol e}^2$
, maternal additive genetic variance; σa,m, direct-maternal additive genetic co-variance; ${\boldsymbol \sigma }_{\boldsymbol e}^2$![]() , residual variance.
, residual variance.
Correlations between traits were estimated by bivariate analyses. The models applied in the bivariate analyses were those selected as best for underlying traits in the univariate analyses (model 4). The matrix notation for the bivariate model was as follows:

where y1 and y2 denote traits 1 and 2, respectively.
Estimates of additive breeding values (EBVs) were derived using the best linear unbiased prediction procedure (BLUP) in WOMBAT (Meyer, Reference Meyer2020). The effect of inclusion of dominance genetic effects in the model on additive breeding values was tested by estimating Spearman correlation coefficients between EBVs obtained with the best model and the best model without dominance genetic effects. It was done for all animals and 10 and 50% of top animals.
Results
Table 2 shows the pedigree structure of the studied population of the Baluchi sheep. The pedigree included 11 658 animals which were progenies of 258 sires and 3137 dams and distributed over 17 generations. Characteristics of the data structure are shown in Table 3. The mean of KR, EF and RGR were 19.81, 456.87% and 1.88, respectively. According to phenotypic coefficient of variation (CV), with 24.16 and 9.77%, EF and KR were, respectively, the most and least variable traits.
Table 2. Pedigree structure of the Baluchi sheep
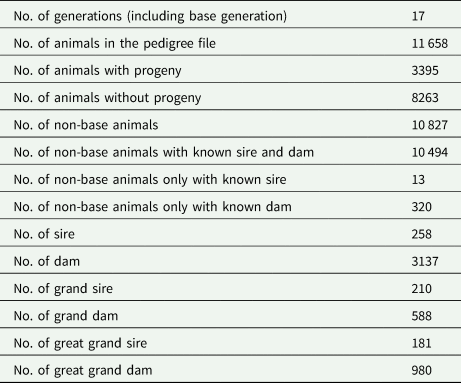
Table 3. Summary statistics for efficiency-related traits in Baluchi sheep
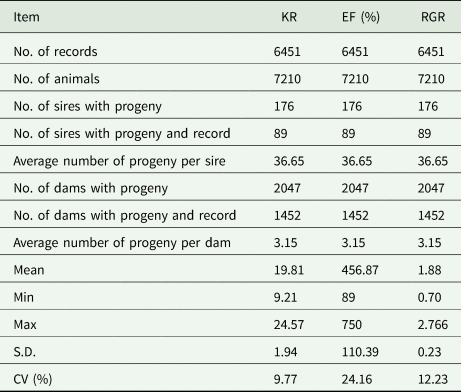
KR, Kleiber ratio; EF, efficiency of growth; RGR, relative growth rate; S.D, standard deviation; CV, phenotypic coefficient of variation.
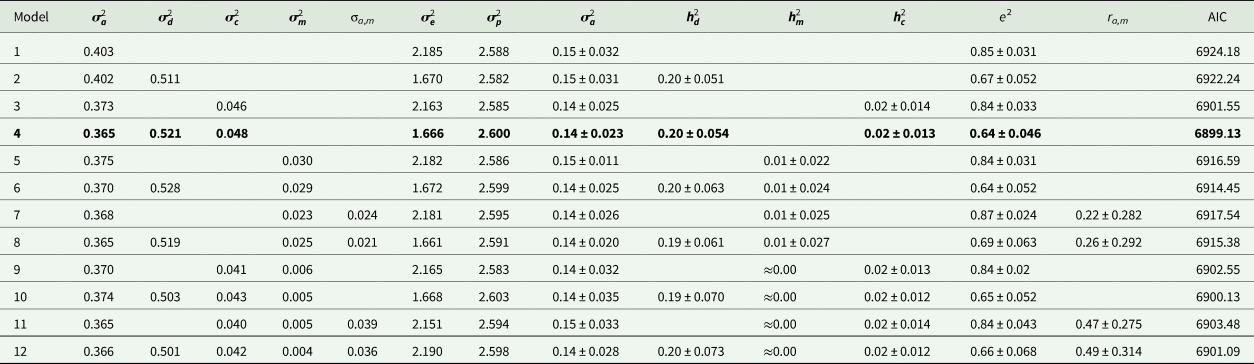
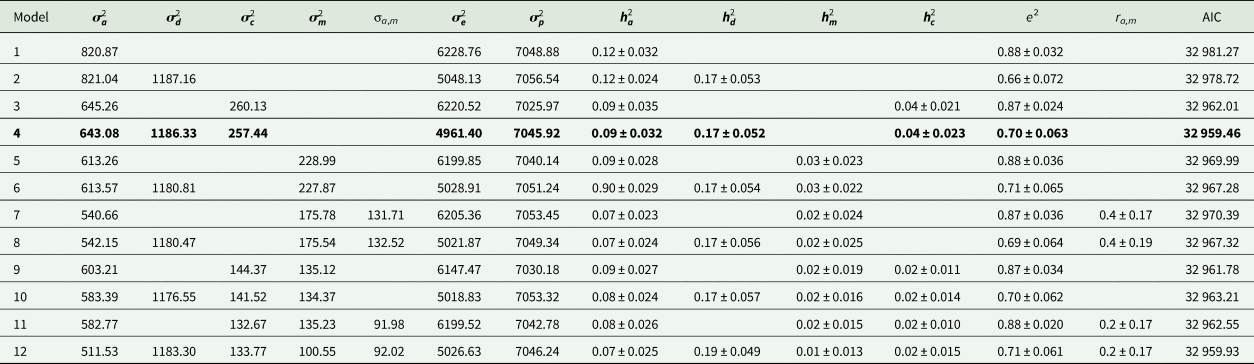
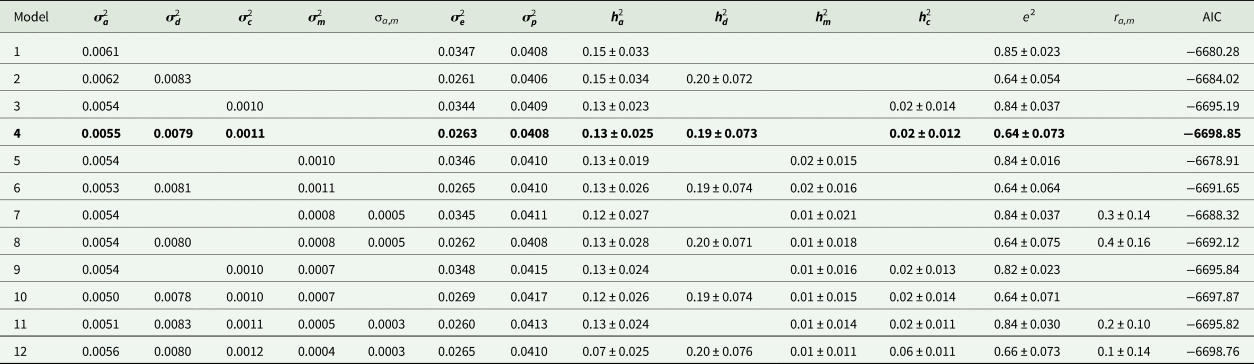
Estimates of variance components and genetic parameters for KR, EF and RGR are listed in Tables 4–6, respectively. For all traits studied, model 1 which included only additive genetic effects had least power to fit the data as evidenced by higher AIC values. Model 3 which contained the maternal permanent environmental effects fitted the data substantially better than model 1, proved by the significant decrease in the AIC. Also it resulted in decrease in additive genetic variance by 7.2, 21.4 and 11.5% for KR, EF and RGR, respectively. Amending models already containing the additive and maternal permanent environmental effects with the dominance genetic effects led to a clearly better fit of data according to the AIC values (model 4). The dominance genetic effects contributed 59, 65 and 59% to the total genetic variance of KR, EF and RGR, respectively. By including dominance genetic effects in the model, additive genetic variance did not change, but residual variance decreased significantly by 24, 19 and 25% for KR, EF and RGR, respectively. In other word, dominance genetic effects distangelled from residual variance. For all traits studied, according to AIC values, model 4 which included additive genetic, dominance genetic and maternal permanent environmental effects described the data best and was selected as the best model.
Table 4. Estimates of variance components and genetic parameters for Kleiber ratio (best model shown in bold)
${\boldsymbol \sigma }_{\boldsymbol a}^2$![]() , additive genetic variance; ${\boldsymbol \sigma }_{\boldsymbol d}^2$
, additive genetic variance; ${\boldsymbol \sigma }_{\boldsymbol d}^2$![]() , dominance genetic variance; ${\boldsymbol \sigma }_{\boldsymbol c}^2$
, dominance genetic variance; ${\boldsymbol \sigma }_{\boldsymbol c}^2$![]() , maternal permanent environmental variance; ${\boldsymbol \sigma }_{\boldsymbol m}^2$
, maternal permanent environmental variance; ${\boldsymbol \sigma }_{\boldsymbol m}^2$![]() , maternal genetic variance; σa,m, direct-maternal additive genetic covariance; ${\boldsymbol \sigma }_{\boldsymbol e}^2$
, maternal genetic variance; σa,m, direct-maternal additive genetic covariance; ${\boldsymbol \sigma }_{\boldsymbol e}^2$![]() , residual variance; ${\boldsymbol \sigma }_{\boldsymbol p}^2$
, residual variance; ${\boldsymbol \sigma }_{\boldsymbol p}^2$![]() , phenotypic variance; ${\boldsymbol h}_{\boldsymbol a}^2$
, phenotypic variance; ${\boldsymbol h}_{\boldsymbol a}^2$![]() , additive heritability; ${\boldsymbol h}_{\boldsymbol d}^2$
, additive heritability; ${\boldsymbol h}_{\boldsymbol d}^2$![]() , dominance heritability; ${\boldsymbol h}_{\boldsymbol c}^2$
, dominance heritability; ${\boldsymbol h}_{\boldsymbol c}^2$![]() , maternal permanent environmental effect; ${\boldsymbol h}_{\boldsymbol m}^2$
, maternal permanent environmental effect; ${\boldsymbol h}_{\boldsymbol m}^2$![]() , maternal heritability; ra,m, direct-maternal additive genetic correlation; AIC, Akaike's information criterion.
, maternal heritability; ra,m, direct-maternal additive genetic correlation; AIC, Akaike's information criterion.
Table 5. Estimates of variance components and genetic parameters for efficiency of growth (best model shown in bold)
${\boldsymbol \sigma }_{\boldsymbol a}^2$![]() , additive genetic variance; ${\boldsymbol \sigma }_{\boldsymbol d}^2$
, additive genetic variance; ${\boldsymbol \sigma }_{\boldsymbol d}^2$![]() , dominance genetic variance; ${\boldsymbol \sigma }_{\boldsymbol c}^2$
, dominance genetic variance; ${\boldsymbol \sigma }_{\boldsymbol c}^2$![]() , maternal permanent environmental variance; ${\boldsymbol \sigma }_{\boldsymbol m}^2$
, maternal permanent environmental variance; ${\boldsymbol \sigma }_{\boldsymbol m}^2$![]() , maternal genetic variance; σa,m, direct-maternal additive genetic covariance; ${\boldsymbol \sigma }_{\boldsymbol e}^2$
, maternal genetic variance; σa,m, direct-maternal additive genetic covariance; ${\boldsymbol \sigma }_{\boldsymbol e}^2$![]() , residual variance; ${\boldsymbol \sigma }_{\boldsymbol p}^2$
, residual variance; ${\boldsymbol \sigma }_{\boldsymbol p}^2$![]() , phenotypic variance; ${\boldsymbol h}_{\boldsymbol a}^2$
, phenotypic variance; ${\boldsymbol h}_{\boldsymbol a}^2$![]() , additive heritability; ${\boldsymbol h}_{\boldsymbol d}^2$
, additive heritability; ${\boldsymbol h}_{\boldsymbol d}^2$![]() , dominance heritability; ${\boldsymbol h}_{\boldsymbol c}^2$
, dominance heritability; ${\boldsymbol h}_{\boldsymbol c}^2$![]() , maternal permanent environmental effect; ${\boldsymbol h}_{\boldsymbol m}^2$
, maternal permanent environmental effect; ${\boldsymbol h}_{\boldsymbol m}^2$![]() , maternal heritability; ra,m, direct-maternal additive genetic correlation; AIC, Akaike's information criterion.
, maternal heritability; ra,m, direct-maternal additive genetic correlation; AIC, Akaike's information criterion.
Table 6. Estimates of variance components and genetic parameters for relative growth rate (best model shown in bold)
${\boldsymbol \sigma }_{\boldsymbol a}^2$![]() , additive genetic variance; ${\boldsymbol \sigma }_{\boldsymbol d}^2$
, additive genetic variance; ${\boldsymbol \sigma }_{\boldsymbol d}^2$![]() , dominance genetic variance; ${\boldsymbol \sigma }_{\boldsymbol c}^2$
, dominance genetic variance; ${\boldsymbol \sigma }_{\boldsymbol c}^2$![]() , maternal permanent environmental variance; ${\boldsymbol \sigma }_{\boldsymbol m}^2$
, maternal permanent environmental variance; ${\boldsymbol \sigma }_{\boldsymbol m}^2$![]() , maternal genetic variance; σa,m, direct-maternal additive genetic covariance; ${\boldsymbol \sigma }_{\boldsymbol e}^2$
, maternal genetic variance; σa,m, direct-maternal additive genetic covariance; ${\boldsymbol \sigma }_{\boldsymbol e}^2$![]() , residual variance; ${\boldsymbol \sigma }_{\boldsymbol p}^2$
, residual variance; ${\boldsymbol \sigma }_{\boldsymbol p}^2$![]() , phenotypic variance; ${\boldsymbol h}_{\boldsymbol a}^2$
, phenotypic variance; ${\boldsymbol h}_{\boldsymbol a}^2$![]() , additive heritability; ${\boldsymbol h}_{\boldsymbol d}^2$
, additive heritability; ${\boldsymbol h}_{\boldsymbol d}^2$![]() , dominance heritability; ${\boldsymbol h}_{\boldsymbol c}^2$
, dominance heritability; ${\boldsymbol h}_{\boldsymbol c}^2$![]() , maternal permanent environmental effect; ${\boldsymbol h}_{\boldsymbol m}^2$
, maternal permanent environmental effect; ${\boldsymbol h}_{\boldsymbol m}^2$![]() , maternal heritability; ra,m, direct-maternal additive genetic correlation; AIC, Akaike's information criterion.
, maternal heritability; ra,m, direct-maternal additive genetic correlation; AIC, Akaike's information criterion.
Estimates of additive heritability $( {\boldsymbol h}_{\boldsymbol a}^2 )$![]() , extracted from the best models, were 0.14 ± 0.02, 0.09 ± 0.03 and 0.13 ± 0.02 for KR, EF and RGR, respectively. Dominance heritability $( {\boldsymbol h}_{\boldsymbol d}^2 )$
, extracted from the best models, were 0.14 ± 0.02, 0.09 ± 0.03 and 0.13 ± 0.02 for KR, EF and RGR, respectively. Dominance heritability $( {\boldsymbol h}_{\boldsymbol d}^2 )$![]() was 0.20 ± 0.05, 0.17 ± 0.05 and 0.19 ± 0.07 for KR, EF and RGR, respectively. Maternal permanent environmental effect $( {\boldsymbol h}_{\boldsymbol c}^2 )$
was 0.20 ± 0.05, 0.17 ± 0.05 and 0.19 ± 0.07 for KR, EF and RGR, respectively. Maternal permanent environmental effect $( {\boldsymbol h}_{\boldsymbol c}^2 )$![]() was 0.02 ± 0.01, 0.04 ± 0.02 and 0.02 ± 0.01 for KR, EF and RGR, respectively.
was 0.02 ± 0.01, 0.04 ± 0.02 and 0.02 ± 0.01 for KR, EF and RGR, respectively.
Correlation between breeding values obtained from the best model (model 4) and the best model without dominance genetic effects (model 3) for all animals, top 50% ranked animals and top 10% ranked animals were large and positive for all traits studied (Table 7), indicating no changes in the EBVs after inclusion of dominance genetic effects in the model. On average, 9.3 animals out of the top 10 animals and 96.3 animals out of the top 100 animals remained in their groups (top 10 and top 100 animals) after including dominance genetic effects in the model (Table 8).
Table 7. Correlations between breeding values predicted by models 3 and 4

KR, Kleiber ratio; EF, efficiency of growth; RGR, relative growth rate.
Table 8. The number of animals that remained in their groups (top 10 and top 100 animals) after including the dominance genetic effects in the model
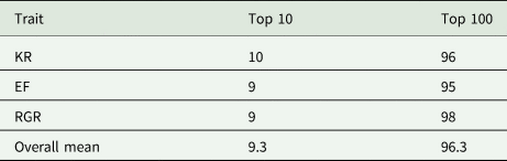
KR, Kleiber ratio; EF, efficiency of growth; RGR, relative growth rate.
Correlations between traits are listed in Table 9. Additive genetic correlation (ra), dominance genetic correlation (rd), maternal permanent environmental correlation (rc) and phenotypic correlation (rp) were all large and positive, ranged from 0.74 ± 0.01 to 0.93 ± 0.21.
Table 9. Correlations between studied traits

ra, additive genetic correlation; rd, dominance genetic correlation; rc, maternal permanent environmental correlation; rp, phenotypic correlation; KR, Kleiber ratio; EF, efficiency of growth; RGR, relative growth rate.
Discussion
In regions where the quantity and quality of available natural feeds are limited, efficiency of feed utilization should be considered in selection programmes. As shown in Table 2, there is variation between animals regarding efficiency of feed utilization. Animals with higher KR, EF and RGR have lower maintenance requirement, i.e. they spend most of the consumed feed on meat production. Since part of this phenotypic variation among animals regarding efficiency-related traits has genetic background, these traits can be improved genetically via selection programmes.
Our findings showed significant contribution of dominance genetic effects to phenotypic variation of efficiency-related traits of Baluchi sheep, more than additive genetic variance. Non-additive genetic effects are usually ignored in animal breeding programmes due to data structure (e.g. incomplete pedigree), computational limitations and over-parameterization of the models (Sadeghi et al., Reference Sadeghi, Rokouei and Faraji-Arough2021). It is the first paper on the importance of dominance genetic effects on efficiency-related traits in sheep. Improvement in general properties of the animal model by including dominance genetic effects has been shown by Jasouri et al. (Reference Jasouri, Zamani and Alijani2017) in chicken and Sadeghi et al. (Reference Sadeghi, Rokouei, Valleh, Abbasi and Faraji-Arough2020) and Sadeghi et al. (Reference Sadeghi, Rokouei and Faraji-Arough2021) in goat. Using genomic data, Karimi et al. (Reference Karimi, Ghafouri-Kesbi and Zamani2023) reported the importance of including dominance genetic effects in genomic selection models. They reported that ignoring dominance genetic effects resulted in inaccurate, biased and dispersed estimates of genomic breeding values.
Previous reports show that including other constituents of genetic variance such as maternal genetic effects (Singh et al., 2016), X chromosome linked genetic effects (Mohammadi and Latifi, Reference Mohammadi and Latifi2020; Noorian et al., Reference Noorian, Joezy-Shekalgorabi and Emam Jomeh Kashan2020) and imprinting effects (Amiri Roudbar et al., Reference Amiri Roudbar, Abdollahi-Arpanahi, Ayatollahi Mehrgardi, Mohammadabadi, Taheri Yeganeh and Rosa2018) in animal model caused a decline in the additive genetic variance and heritability estimates. But our results showed a different behaviour for dominance genetic variance as it distangelled from the residual variance and did not affect the additive genetic variance. Heidaritabar et al. (Reference Heidaritabar, Wolc, Arango, Zeng, Settar, Fulton, O'Sullivan, Bastiaansen, Fernando and Garrick2016) reported that dominance and epistasis effects were important for egg production traits in layers and when these effects were ignored from the genomic evaluation models, they were accumulated in residual variance. In Adani goat, Sadeghi et al. (Reference Sadeghi, Rokouei, Valleh, Abbasi and Faraji-Arough2020) studied the effect of dominance genetic effects on body weight traits and reported that by including dominance genetic effects, residual variance decreased in a range between 28.2% (weaning weight) and 59.2% (birth weight). Also, Sadeghi et al. (Reference Sadeghi, Rokouei and Faraji-Arough2021) reported decrease in residual variance between 20.6% (average daily gain from 6 to 9 months of age) and 50.21% (average daily gain from weaning to 3 months of age) in Adani goat. These results confirm our findings. Decrease in residual variance is an indicator of improvement in general properties of the model. By decrease in residual variance, the $\sigma _a^2 /\sigma _e^2$![]() ratio increased. Whenever this ratio is low, phenotypic response to selection would be slower because environmental variation could offset phenotypic response to selection even when there is high additive variation in the trait of interest (Ghafouri-Kesbi and Notter, Reference Ghafouri-Kesbi and Notter2016).
ratio increased. Whenever this ratio is low, phenotypic response to selection would be slower because environmental variation could offset phenotypic response to selection even when there is high additive variation in the trait of interest (Ghafouri-Kesbi and Notter, Reference Ghafouri-Kesbi and Notter2016).
There is no previous report on dominance heritability for efficiency-related traits in sheep which makes comparison difficult. In other livestock, however, dominance heritability has been estimated for economic traits. For example, Heidaritabar et al. (Reference Heidaritabar, Wolc, Arango, Zeng, Settar, Fulton, O'Sullivan, Bastiaansen, Fernando and Garrick2016) in brown layers estimated ${\boldsymbol h}_{\boldsymbol d}^2$![]() for egg production, average egg weight, albumin height, egg colour, yolk weight and age at sexual maturity as 0.14, 0.22, 0.22, 0.20, 0.13 and 0.13, respectively. Jasouri et al. (Reference Jasouri, Zamani and Alijani2017) investigated the contribution of dominance genetic effects to phenotypic variation of body weight traits and egg production traits of Iranian native fowl and reported ${\boldsymbol h}_{\boldsymbol d}^2$
for egg production, average egg weight, albumin height, egg colour, yolk weight and age at sexual maturity as 0.14, 0.22, 0.22, 0.20, 0.13 and 0.13, respectively. Jasouri et al. (Reference Jasouri, Zamani and Alijani2017) investigated the contribution of dominance genetic effects to phenotypic variation of body weight traits and egg production traits of Iranian native fowl and reported ${\boldsymbol h}_{\boldsymbol d}^2$![]() for body weight at birth, 8 and 12 weeks of age as 0.06, 0.08 and 0.01, respectively. In addition, for the age at sexual maturity, average egg weight and number of eggs, ${\boldsymbol h}_{\boldsymbol d}^2$
for body weight at birth, 8 and 12 weeks of age as 0.06, 0.08 and 0.01, respectively. In addition, for the age at sexual maturity, average egg weight and number of eggs, ${\boldsymbol h}_{\boldsymbol d}^2$![]() was 0.06, 0.06 and 0.08, respectively. In Adani goats, Sadeghi et al. (Reference Sadeghi, Rokouei, Valleh, Abbasi and Faraji-Arough2020) estimated ${\boldsymbol h}_{\boldsymbol d}^2$
was 0.06, 0.06 and 0.08, respectively. In Adani goats, Sadeghi et al. (Reference Sadeghi, Rokouei, Valleh, Abbasi and Faraji-Arough2020) estimated ${\boldsymbol h}_{\boldsymbol d}^2$![]() for body weight at birth, weaning, 6, 9 and 12 months of age as 0.15, 0.17, 0.11, 0.19 and 0.25, respectively. For these traits, the additive heritability $( {\boldsymbol h}_{\boldsymbol a}^2 )$
for body weight at birth, weaning, 6, 9 and 12 months of age as 0.15, 0.17, 0.11, 0.19 and 0.25, respectively. For these traits, the additive heritability $( {\boldsymbol h}_{\boldsymbol a}^2 )$![]() was in the range between 0.17 (weaning weight) and 0.38 (birth weight). Sadeghi et al. (Reference Sadeghi, Rokouei and Faraji-Arough2021) estimated ${\boldsymbol h}_{\boldsymbol d}^2$
was in the range between 0.17 (weaning weight) and 0.38 (birth weight). Sadeghi et al. (Reference Sadeghi, Rokouei and Faraji-Arough2021) estimated ${\boldsymbol h}_{\boldsymbol d}^2$![]() for pre- and post-weaning average daily gain of Adani goat as 0.15 and 0.11, respectively. Current results and other reports show that part of phenotypic variation in economic traits of livestock has dominance genetic background which is comparable with additive genetic effects. However, our results contradicted other reports showing smaller dominance heritability compared with additive heritability for growth-related traits in goat (Sadeghi et al., Reference Sadeghi, Rokouei, Valleh, Abbasi and Faraji-Arough2020; Sadeghi et al., Reference Sadeghi, Rokouei and Faraji-Arough2021) and growth and egg production traits in chicken (Heidaritabar et al., Reference Heidaritabar, Wolc, Arango, Zeng, Settar, Fulton, O'Sullivan, Bastiaansen, Fernando and Garrick2016; Jasouri et al., Reference Jasouri, Zamani and Alijani2017). One of Fisher's hypotheses associated with his theory of dominance (Fisher, Reference Fisher1958) predicted that traits closely associated with fitness should have a significant dominance variance component, both due to the erosion of the additive component of variance and the evolution of directional dominance. Efficiency-related traits may have been correlated with fitness in the ancestral populations from which the contemporary Baluchi sheep has been drawn.
for pre- and post-weaning average daily gain of Adani goat as 0.15 and 0.11, respectively. Current results and other reports show that part of phenotypic variation in economic traits of livestock has dominance genetic background which is comparable with additive genetic effects. However, our results contradicted other reports showing smaller dominance heritability compared with additive heritability for growth-related traits in goat (Sadeghi et al., Reference Sadeghi, Rokouei, Valleh, Abbasi and Faraji-Arough2020; Sadeghi et al., Reference Sadeghi, Rokouei and Faraji-Arough2021) and growth and egg production traits in chicken (Heidaritabar et al., Reference Heidaritabar, Wolc, Arango, Zeng, Settar, Fulton, O'Sullivan, Bastiaansen, Fernando and Garrick2016; Jasouri et al., Reference Jasouri, Zamani and Alijani2017). One of Fisher's hypotheses associated with his theory of dominance (Fisher, Reference Fisher1958) predicted that traits closely associated with fitness should have a significant dominance variance component, both due to the erosion of the additive component of variance and the evolution of directional dominance. Efficiency-related traits may have been correlated with fitness in the ancestral populations from which the contemporary Baluchi sheep has been drawn.
Spearman correlation between the additive breeding values from models with and without the dominance genetic effects was high and close to unity, which implied that the additive estimated breeding values between models are coherent. A correlation lower than 1.00 means that ranking of animals may change across models. Toro and Varona (Reference Toro and Varona2010) stated that considering the effects of non-additive genetic effects in genomic evaluation models reduces error and increases the accuracy of estimated breeding values which reflected in greater expected response to selection. Sadeghi et al. (Reference Sadeghi, Rokouei, Valleh, Abbasi and Faraji-Arough2020) and Sadeghi et al. (Reference Sadeghi, Rokouei and Faraji-Arough2021) reported increase in accuracy of additive breeding values after including dominance effect in the model for genetic evaluation of Adani goat for body weight and average daily gain. Of course, they did not study the change in ranking of animals across models with and without dominance effect. As a result, inclusion of dominance effect did not change ranking of top animals but has the potential to increase the accuracy of additive breeding values which is relevant to maximize genetic progress (Legarra and Reverter, Reference Legarra and Reverter2018). Therefore, it seems reasonable to recommend inclusion of dominance genetic effects in the model for genetic evaluation of Baluchi lambs for efficiency-related traits.
Genetic correlation is the correlation of phenotypic effects by genetic variants across the genome on two phenotypes. It quantifies the overall genetic similarity and provides insights into the polygenic genetic architecture of complex traits (Zhang et al., Reference Zhang, Cheng, Jiang, Ye, Lu and Zhao2021). A positive genetic correlation between efficiency-related traits allows improving all traits simultaneously and that one of them is enough to be in the multi-trait selection programmes. In agreement with our findings, in Baluchi sheep, Ghafouri-Kesbi and Gholizadeh (Reference Ghafouri-Kesbi and Gholizadeh2017) estimated additive genetic correlation between pre-weaning KR and pre-weaning EF and RGR as 0.89 and 0.65, respectively. Dominance genetic correlations between studied traits were positive and high. Lack of previous reports on dominance genetic correlations between economic traits in livestock makes comparison difficult. Considering KR and EF, positive additive genetic correlation means that the value of KR in parents is correlated to the value of EF in offspring. Regarding dominance genetic correlation, the value of KR in the parent does not correlate to the EF value in offspring. While the additive genetic correlation would accelerate the response (if both traits were under the same direction of selection), the dominance correlation is not heritable, so it does not contribute to the response to selection (and hence doesn't accelerate the response).
In conclusion, all efficiency-related traits were affected by dominance genetic effects, with contributions more than additive genetic and maternal effects. Models with dominance genetic effects fitted the data substantially better than otherwise identical models. Accounting for the dominance genetic effects in the model led to significant decrease in residual variance which was an indicator of improvement in general properties of the model. Dominance correlations between traits were positively high. Correlation between breeding values estimated by models with and without dominance effects were close to unity, indicating a little chance for re-ranking of top animals after inclusion of dominance genetic effect in the model. However, since inclusion of dominance genetic effect in the model resulted in better data fit, improvement in general properties of the model and increase in the accuracy of breeding values, inclusion of these effects in the genetic evaluation models in sheep would be useful.
Acknowledgements
The staff of Abbasabad Baluchi sheep breeding station are gratefully acknowledged for providing us with the data used in the current study.
Author contributions
F. Ghafouri-Kesbi: designed the study, analysed the data, wrote and revised the manuscript. M. Gholizadeh: provided the data, analysed the data.
Funding statement
This research received no specific grant from any funding agency, commercial or not-for-profit sectors.
Competing interests
The authors declare no conflicts of interest between authors and between authors and other people, institutions or organizations.
Ethical standards
Not applicable.