Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Tomkins, R. J.
1976.
On the growth rate of weighted averages of exponential random variables.
Acta Mathematica Academiae Scientiarum Hungaricae,
Vol. 27,
Issue. 1-2,
p.
97.
O'Brien, G. L.
1977.
Path properties of successive sample minima from stationary processes.
Zeitschrift f�r Wahrscheinlichkeitstheorie und Verwandte Gebiete,
Vol. 38,
Issue. 4,
p.
313.
Hall, Peter
1979.
On the relative stability of large order statistics.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 86,
Issue. 3,
p.
467.
H�sler, J.
1981.
The law of the iterated logarithm for the last exit time of independent random sequences.
Zeitschrift f�r Wahrscheinlichkeitstheorie und Verwandte Gebiete,
Vol. 57,
Issue. 3,
p.
397.
Hüsler, Jürg
1985.
The growth rate of partial maxima on subsequences.
Statistics & Probability Letters,
Vol. 3,
Issue. 5,
p.
245.
Davis, Richard A.
Mulrow, Edward
and
Resnick, Sidney I.
1988.
Almost sure limit sets of random samples in ℝd.
Advances in Applied Probability,
Vol. 20,
Issue. 3,
p.
573.
Gather, U.
and
Rauhut, B.
1990.
The outlier behaviour of probability distributions.
Journal of Statistical Planning and Inference,
Vol. 26,
Issue. 2,
p.
237.
Gut, Allan
1990.
Limit points of sample maxima.
Statistics & Probability Letters,
Vol. 9,
Issue. 4,
p.
331.
Tomkins, R.J.
and
Wang, Hong
1992.
Stability theorems for large order statistics with varying ranks.
Statistics & Probability Letters,
Vol. 14,
Issue. 2,
p.
91.
F.Li, Michael Z.
and
Tomkins, R. J.
1992.
Stability theorems for maxima of dependent sequences.
Canadian Journal of Statistics,
Vol. 20,
Issue. 2,
p.
211.
Nayak, S.S.
and
Wali, K.S.
1992.
On the number of boundary crossings related to LIL and SLLN for record values and partial maxima of i.i.d. sequences and extremes of uniform spacings.
Stochastic Processes and their Applications,
Vol. 43,
Issue. 2,
p.
317.
Molchanov, Ilya S.
1993.
Strong law of large numbers for unions of random closed sets.
Stochastic Processes and their Applications,
Vol. 46,
Issue. 2,
p.
199.
Mcbeth, Douglas
and
Resnick, Sidney
1994.
Stability of random sets generated by multivariate samples.
Communications in Statistics. Stochastic Models,
Vol. 10,
Issue. 3,
p.
549.
Tomkins, R. J.
1996.
Rates of convergence for the stability of large order statistics.
Journal of Theoretical Probability,
Vol. 9,
Issue. 4,
p.
841.
Goldie, Charles M.
and
Maller, Ross A.
1996.
A point-process approach to almost-sure behaviour of record values and order statistics.
Advances in Applied Probability,
Vol. 28,
Issue. 2,
p.
426.
Tomkins, R.J.
1999.
Regular stability of large order statistics.
Statistics & Probability Letters,
Vol. 41,
Issue. 2,
p.
145.
Fahrner, Ingo
2000.
An extension of the almost sure max–limit theorem.
Statistics & Probability Letters,
Vol. 49,
Issue. 1,
p.
93.
Barme-Delcroix, Marie-Françoise
and
Brito, Margarida
2001.
Multivariate Stability and Strong Limiting Behaviour of Intermediate Order Statistics.
Journal of Multivariate Analysis,
Vol. 79,
Issue. 2,
p.
157.
Naveau, Philippe
2003.
Almost sure relative stability of the maximum of a stationary sequence.
Advances in Applied Probability,
Vol. 35,
Issue. 03,
p.
721.
Li, Michael Z. F.
and
Tomkins, R. J.
2004.
Stability of Maxima of Random Variables with Multidimensional Indices.
Extremes,
Vol. 7,
Issue. 2,
p.
135.
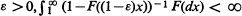 and in this case bn ∼ F– 1 (1 – 1/n) Necessary and sufficient conditions for lim supn→∞ , Mn /bn = l > 1 a.s. are given and this is shown to be insufficient in general for lim infn→∞ Mn /bn = 1 a.s. except when l = 1. When the Xn are r.v.'s defined on a finite Markov chain, one shows by means of an analogue of the Borel Zero-One Law and properties of semi-Markov matrices that the stability problem for this case can be reduced to the i.i.d. case.
and in this case bn ∼ F– 1 (1 – 1/n) Necessary and sufficient conditions for lim supn→∞ , Mn /bn = l > 1 a.s. are given and this is shown to be insufficient in general for lim infn→∞ Mn /bn = 1 a.s. except when l = 1. When the Xn are r.v.'s defined on a finite Markov chain, one shows by means of an analogue of the Borel Zero-One Law and properties of semi-Markov matrices that the stability problem for this case can be reduced to the i.i.d. case.
