Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Horváth, Lajos
1984.
Strong approximation of certain stopped sums.
Statistics & Probability Letters,
Vol. 2,
Issue. 3,
p.
181.
Niculescu, Ştefan P.
1984.
On the asymptotic distribution of multivariate renewal processes.
Journal of Applied Probability,
Vol. 21,
Issue. 03,
p.
639.
Roginsky, Allen L.
1992.
A central limit theorem by remainder term for renewal processes.
Advances in Applied Probability,
Vol. 24,
Issue. 2,
p.
267.
Steinebach, Josef
and
Eastwood, Vera R.
1997.
Detecting changes in a multivariate renewal process.
Metrika,
Vol. 46,
Issue. 1,
p.
1.

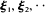 ·be a sequence of
·be a sequence of 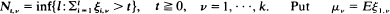 for
for 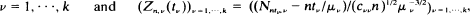 where (
where (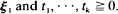 In this paper the weak convergence of Z
In this paper the weak convergence of Z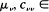 (0,∞) for all
(0,∞) for all 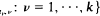 for fixed
for fixed 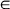 [0,∞)
[0,∞)