Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-10T14:08:11.214Z Has data issue: false hasContentIssue false
  • English
  • Français

Asymptotic behavior and quasi-limiting distributions on time-fractional birth and death processes

Part of: Stochastic processes Special processes

Published online by Cambridge University Press:  11 November 2022

Jorge Littin Curinao Open the ORCID record for Jorge Littin Curinao [Opens in a new window]
Jorge Littin Curinao*
Affiliation:
Universidad Católica del Norte
*
*Postal address: Departamento de Matemáticas, Universidad Católica del Norte, Angamos 0610, Antofagasta, Chile. Email address: jlittin@ucn.cl
Get access Rights & Permissions [Opens in a new window]

Abstract

In this article we provide new results for the asymptotic behavior of a time-fractional birth and death process 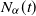$N_{\alpha}(t)$ , whose transition probabilities 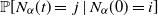$\mathbb{P}[N_{\alpha}(t)=\,j\mid N_{\alpha}(0)=i]$ are governed by a time-fractional system of differential equations, under the condition that it is not killed. More specifically, we prove that the concepts of quasi-limiting distribution and quasi-stationary distribution do not coincide, which is a consequence of the long-memory nature of the process. In addition, exact formulas for the quasi-limiting distribution and its rate convergence are presented. In the first sections, we revisit the two equivalent characterizations for this process: the first one is a time-changed classic birth and death process, whereas the second one is a Markov renewal process. Finally, we apply our main theorems to the linear model originally introduced by Orsingher and Polito [23].

Keywords

Fractional processesquasi-limiting distributionsinverse stable subordinators

MSC classification

Primary: 60G22: Fractional processes, including fractional Brownian motion
Secondary: 60G18: Self-similar processes 60K15: Markov renewal processes, semi-Markov processes
Type
Original Article
Information
Journal of Applied Probability , Volume 59 , Issue 4 , December 2022 , pp. 1199 - 1227
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bailey, N. T. J. (1964). The Elements of Stochastic Processes: With Applications to Natural Sciences. John Wiley.Google Scholar
Bertoin, J. (1995). Some applications of subordinators to local times of Markov processes. Forum Math 7, 629–644.CrossRefGoogle Scholar
Bertoin, J. (1999). Subordinators: Examples and Applications. Springer, Berlin and Heidelberg.Google Scholar
Çinlar, E. (2013). Introduction to Stochastic Processes (Dover Books on Mathematics Series). Dover Publications.Google Scholar
Collet, P., Martínez, S. and San Martín, J. (1995). Asymptotic laws for one-dimensional diffusions conditioned to nonabsorption. Ann. Prob. 23, 1300–1314.CrossRefGoogle Scholar
Collet, P., Martínez, S. and San Martín, J. (2012). Quasi-Stationary Distributions: Markov Chains, Diffusions and Dynamical Systems (Probability and its Applications). Springer, Berlin and Heidelberg.Google Scholar
Darroch, J. N. and Seneta, E. (1967). On quasi-stationary distributions in absorbing continuous-time finite Markov chains. J. Appl. Prob. 4, 192–196.CrossRefGoogle Scholar
van Doorn, E. A. (1991). Quasi-stationary distributions and convergence to quasi-stationarity of birth–death processes. Adv. Appl. Prob. 23, 683–700.CrossRefGoogle Scholar
van Doorn, E. A. (2012). Conditions for the existence of quasi-stationary distributions for birth–death processes with killing. Stoch. Process. Appl. 122, 2400–2410.CrossRefGoogle Scholar
van Doorn, E. A. and Pollett, P. K. (2013). Quasi-stationary distributions for discrete-state models. Europ. J. Operat. Res. 230, 1–14.CrossRefGoogle Scholar
Ferrari, P. A., Kesten, H., Martínez, S. and Picco, P. (1995). Existence of quasi-stationary distributions: A renewal dynamical approach. Ann. Prob. 23, 501–521.CrossRefGoogle Scholar
Gorenflo, R., Kilbas, A., Mainardi, F. and Rogosin, S. V. (2014). Mittag–Leffler Functions, Related Topics and Applications. Springer.CrossRefGoogle Scholar
Jumarie, J. (2010). Fractional multiple birth–death processes with birth probabilities $\lambda_i({\Delta}t)^\alpha+o(({\Delta}t)^\alpha)$ . J. Franklin Inst. 347, 1797–1813.CrossRefGoogle Scholar
Karlin, S. and McGregor, J. L. (1957). The differential equations of birth-and-death processes, and the Stieltjes moment problem. Trans. Amer. Math. Soc. 85, 489–546.CrossRefGoogle Scholar
Mandl, P. (1961). Spectral theory of semi-groups connected with diffusion processes and its application. Czechoslovak. Math. J. 11, 558–569.CrossRefGoogle Scholar
Martínez, S. and San Martín, J. (1994). Quasi-stationary distributions for a Brownian motion with drift and associated limit laws. J. Appl. Prob. 31, 911–920.CrossRefGoogle Scholar
Martínez, S., Picco, P. and San Martín, J. (1998). Domain of attraction of quasi-stationary distributions for the Brownian motion with drift. Adv. Appl. Prob. 30, 385–408.CrossRefGoogle Scholar
Meerschaert, M. and Scheffler, H. P. (2004). Limit theorems for continuous-time random walks with infinite mean waiting times. J. Appl. Prob. 41, 623–638.CrossRefGoogle Scholar
Meerschaert, M. and Straka, P. (2013). Inverse stable subordinators. Math. Model. Nat. Phenom. 8, 1–16.CrossRefGoogle ScholarPubMed
Meerschaert, M., Nane, E. and Vellaisamy, P. (2011). The fractional Poisson process and the inverse stable subordinator. Electron. J. Prob. 16, 1600–1620.CrossRefGoogle Scholar
Orsingher, E. and Beghin, L. (2004). Time-fractional telegraph equations and telegraph processes with Brownian time. Prob. Theory Relat. Fields 128, 141–160.CrossRefGoogle Scholar
Orsingher, E. and Beghin, L. (2009). Fractional diffusion equations and processes with randomly varying time. Ann. Prob. 37, 206–249.CrossRefGoogle Scholar
Orsingher, E. and Polito, F. (2011). On a fractional linear birth–death process. Bernoulli 17, 114–137.CrossRefGoogle Scholar
Seneta, E. and Vere-Jones, D. (1966). On quasi-stationary distributions in discrete-time Markov chains with a denumerable infinity of states. J. Appl. Prob. 3, 403–434.CrossRefGoogle Scholar
Yaglom, A. M. (1947). Certain limit theorems of the theory of branching random processes. Dokl. Akad. Nauk SSSR 56, 795–798.Google Scholar