Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-10T15:13:19.616Z Has data issue: false hasContentIssue false
  • English
  • Français

Asymptotic results on Hoppe trees and their variations

Part of: Graph theory Combinatorial probability

Published online by Cambridge University Press:  16 July 2020

Ella Hiesmayr  and
Ümit Işlak
Ella Hiesmayr*
Affiliation:
University of California, Berkeley
Ümit Işlak*
Affiliation:
Boğaziçi University
*
*Postal address: University of California, Berkeley, U.S. Email: ella.hiesmayr@berkeley.edu
**Postal address: Boğaziçi University, Istanbul, Turkey. Email: umit.islak1@boun.edu.tr
Get access Rights & Permissions [Opens in a new window]

Abstract

A uniform recursive tree on n vertices is a random tree where each possible 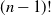$(n-1)!$ labelled recursive rooted tree is selected with equal probability. We introduce and study weighted trees, a non-uniform recursive tree model departing from the recently introduced Hoppe trees. This class generalizes both uniform recursive trees and Hoppe trees, providing diversity among the nodes and making the model more flexible for applications. We analyse the number of leaves, the height, the depth, the number of branches, and the size of the largest branch in these weighted trees.

Keywords

Uniform recursive treesHoppe treesEwens sampling formularandom permutationscouplingrandom tree statistics

MSC classification

Primary: 05C80: Random graphs
Secondary: 60C05: Combinatorial probability
Type
Research Papers
Information
Journal of Applied Probability , Volume 57 , Issue 2 , June 2020 , pp. 441 - 457
Copyright
© Applied Probability Trust 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Altok, S. and Işlak, Ü. (2017). On leaf related statistics in recursive tree models. Statist. Prob. Lett. 121, 61–69.CrossRefGoogle Scholar
Arratia, R., Barbour, A. and Tavaré, S. (2003). Logarithmic Combinatorial Structures: A Probabilistic Approach. European Mathematical Society, Zürich.CrossRefGoogle Scholar
Bergeron, F., Flajolet, P. and Salvy, B. (1992). Varieties of increasing trees. In Proc. 17th Colloq. Trees in Algebra and Programming, pp. 24–48.CrossRefGoogle Scholar
Devroye, L., Fawzi, O. and Fraiman, N. (2011). Depth properties of scaled attachment random recursive trees. Random Structures Algorithms 41, 66–98.CrossRefGoogle Scholar
Drmota, M. (2009). Random Trees: An Interplay between Combinatorics and Probability. Springer, Vienna.CrossRefGoogle Scholar
Feng, Q., Su, C. and Hu, Z. (2005). Branching structure of uniform recursive trees. Science China Ser. A 48, 769–784.CrossRefGoogle Scholar
Finch, S. R. (2003). Mathematical Constants. Cambridge University Press.Google Scholar
Gastwirth, J. L. (1977). A probability model of a pyramid scheme. Amer. Statistician 31, 79–82.Google Scholar
Hiesmayr, E. (2017). On asymptotics of two non-uniform recursive tree models. Master’s thesis. Available at https://arxiv.org/abs/1710.01402.Google Scholar
Leckey, K. and Neininger, R. (2013). Asymptotic analysis of Hoppe trees. J. Appl. Prob. 50, 228–238.CrossRefGoogle Scholar
Smythe, R. T. and Mahmoud, H. M. (1995). A survey of recursive trees. Theory Prob. Math. Statist. 51, 1–27.Google Scholar
Marzouk, C. (2016). Fires on large recursive trees. Stoch. Process. Appl. 126, 265–289.CrossRefGoogle Scholar
Najock, D. and Heyde, C. C. (1982). On the number of terminal vertices in certain random trees with an application to stemma construction in philology. J. Appl. Prob. 19, 675–680.CrossRefGoogle Scholar
Pittel, B. (1994). Note on the heights of random recursive trees and random m-ary search trees. Random Structures Algorithms. 5, 337–347.CrossRefGoogle Scholar
Ross, N. (2011). Fundamentals of Stein’s method. Prob. Surv. 8, 210–293.CrossRefGoogle Scholar
Szymanski, J. (1987). On a nonuniform random recursive tree. In Annals of Discrete Mathematics 33, ed. Barlotti, A., Biliotti, M., Cossu, A., Korchmaros, G., and Tallini, G., North-Holland, Amsterdam, pp. 297–306.CrossRefGoogle Scholar