Article contents
Bounds for expected supremum of fractional Brownian motion with drift
Published online by Cambridge University Press: 23 June 2021
Abstract
We provide upper and lower bounds for the mean 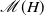 $\mathscr{M}(H)$ of
$\mathscr{M}(H)$ of 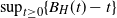 $\sup_{t\geq 0} \{B_H(t) - t\}$, with
$\sup_{t\geq 0} \{B_H(t) - t\}$, with 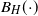 $B_H(\!\cdot\!)$ a zero-mean, variance-normalized version of fractional Brownian motion with Hurst parameter
$B_H(\!\cdot\!)$ a zero-mean, variance-normalized version of fractional Brownian motion with Hurst parameter 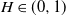 $H\in(0,1)$. We find bounds in (semi-) closed form, distinguishing between
$H\in(0,1)$. We find bounds in (semi-) closed form, distinguishing between 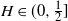 $H\in(0,\frac{1}{2}]$ and
$H\in(0,\frac{1}{2}]$ and 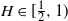 $H\in[\frac{1}{2},1)$, where in the former regime a numerical procedure is presented that drastically reduces the upper bound. For
$H\in[\frac{1}{2},1)$, where in the former regime a numerical procedure is presented that drastically reduces the upper bound. For 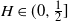 $H\in(0,\frac{1}{2}]$, the ratio between the upper and lower bound is bounded, whereas for
$H\in(0,\frac{1}{2}]$, the ratio between the upper and lower bound is bounded, whereas for 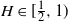 $H\in[\frac{1}{2},1)$ the derived upper and lower bound have a strongly similar shape. We also derive a new upper bound for the mean of
$H\in[\frac{1}{2},1)$ the derived upper and lower bound have a strongly similar shape. We also derive a new upper bound for the mean of 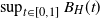 $\sup_{t\in[0,1]} B_H(t)$,
$\sup_{t\in[0,1]} B_H(t)$, 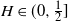 $H\in(0,\frac{1}{2}]$, which is tight around
$H\in(0,\frac{1}{2}]$, which is tight around 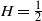 $H=\frac{1}{2}$.
$H=\frac{1}{2}$.
MSC classification
Information
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press on behalf of Applied Probability Trust
References
- 5
- Cited by


