Article contents
A cost relationship between age and block replacement policies
Published online by Cambridge University Press: 14 July 2016
Abstract
The general cost structure of a unit on line is assumed to be governed by a stochastic process 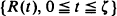 , where R(t) denotes the operating cost on [0, t)and ζ denotes the time of an unscheduled (or unplanned) replacement by a new unit at a cost c 1. For an age replacement maintenance policy, scheduled (or planned) replacements occur whenever an operating unit reaches age T, whereas in the block replacement case, scheduled replacements occur every T units of time. Such scheduled replacements cost c2. The expected long-run cost per unit time can then be expressed in the form A(T)/Ε [min(ζ, T)] and B(T)/T respectively. Our main result shows that
, where R(t) denotes the operating cost on [0, t)and ζ denotes the time of an unscheduled (or unplanned) replacement by a new unit at a cost c 1. For an age replacement maintenance policy, scheduled (or planned) replacements occur whenever an operating unit reaches age T, whereas in the block replacement case, scheduled replacements occur every T units of time. Such scheduled replacements cost c2. The expected long-run cost per unit time can then be expressed in the form A(T)/Ε [min(ζ, T)] and B(T)/T respectively. Our main result shows that 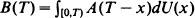 where U is the associated renewal function generated by ζ.
where U is the associated renewal function generated by ζ.
Information
- Type
- Research Papers
- Information
- Copyright
- Copyright © Applied Probability Trust 1988
Footnotes
Research supported by ONR Contract N0014–84-K-0084 and AFOSR Grant AFOSR-84–0113.
References
- 15
- Cited by

