Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Sudbury, Aidan
1993.
The survival of various interacting particle systems.
Advances in Applied Probability,
Vol. 25,
Issue. 04,
p.
1010.
Liggett, T. M.
1994.
Probability and Phase Transition.
p.
209.
Sudbury, Aidan
1997.
The convergence of the biased annihilating branching process and the double-flipping process in Zd.
Stochastic Processes and their Applications,
Vol. 68,
Issue. 2,
p.
255.
Lloyd, Peter
and
Sudbury, Aidan
1997.
Quantum operators in classical probability theory. IV. Quasi-duality and thinnings of interacting particle systems.
The Annals of Probability,
Vol. 25,
Issue. 1,
Sudbury, Aidan
1999.
Hunting submartingales in the jumping voter model and the biased annihilating branching process.
Advances in Applied Probability,
Vol. 31,
Issue. 3,
p.
839.
Neuhauser, Claudia
1999.
Perplexing Problems in Probability.
p.
355.

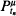 , for a sequence of times tending to infinity, must be invariant. This result is used to show that the one-dimensional biased annihilating branching process with parameter > 1/3 converges in distribution to the upper invariant measure provided its initial configuration is almost surely finite and non-null.
, for a sequence of times tending to infinity, must be invariant. This result is used to show that the one-dimensional biased annihilating branching process with parameter > 1/3 converges in distribution to the upper invariant measure provided its initial configuration is almost surely finite and non-null.