Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Pakes, Anthony G.
and
Heyde, C. C.
1982.
Optimal estimation of the criticality parameter of a supercritical branching process having random environments.
Journal of Applied Probability,
Vol. 19,
Issue. 02,
p.
415.
Harrington, David P.
and
Fleming, Thomas R.
1982.
Statistical properties of estimators for continuous time Markov branching processes with varying and random environments.
Mathematical Biosciences,
Vol. 58,
Issue. 1,
p.
111.
Vatutin, V. A.
and
Zubkov, A. M.
1993.
Branching processes. II.
Journal of Soviet Mathematics,
Vol. 67,
Issue. 6,
p.
3407.
DAVIDSON, IAN
SHINOZAWA, YOSHIKATSU
and
TIPPETT, MARK
2009.
Capital Project Analysis When Cash Flows Evolve as a Continuous Time Branching Process.
Abacus,
Vol. 45,
Issue. 1,
p.
44.
2010.
Introduction to Stochastic Models.
p.
343.
Vidyashankar, Anand N.
and
Li, Lei
2019.
Ancestral inference for branching processes in random environments and an application to polymerase chain reaction.
Stochastic Models,
Vol. 35,
Issue. 3,
p.
318.

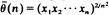 when
when 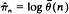 is a strongly consistent and asymptotically unbiased estimator for the criticality parameter
is a strongly consistent and asymptotically unbiased estimator for the criticality parameter