No CrossRef data available.
Article contents
The expected number of visits of a sequence of normal partial sums to each side of a boundary
Published online by Cambridge University Press: 14 July 2016
Abstract
Let 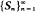 be the sequence of partial sums of independent N(μ, 1) random variables. The boundary in the {(n, Sn )} plane which minimizes the expected number of times n that Sn will be below a boundary when μ = θ > 0 subject to a given expected number of visits that Sn will be above the same boundary when μ = 0 is shown to be linear and is also characterized. Similar results are shown for Brownian motion.
be the sequence of partial sums of independent N(μ, 1) random variables. The boundary in the {(n, Sn )} plane which minimizes the expected number of times n that Sn will be below a boundary when μ = θ > 0 subject to a given expected number of visits that Sn will be above the same boundary when μ = 0 is shown to be linear and is also characterized. Similar results are shown for Brownian motion.
Keywords
Information
- Type
- Short Communications
- Information
- Copyright
- Copyright © Applied Probability Trust 1978
References
Feller, W. (1971) An Introduction to Probability Theory and its Applications, Vol. II. Wiley, New York.Google Scholar
Pollar, M. (1978) Optimality and almost optimality of mixture stopping rules. Ann. Statist.
To appear.CrossRefGoogle Scholar
Robbins, H. and Siegmund, D. (1970) Boundary crossing probabilities for the Wiener process and sample sums. Ann. Math. Statist.
41, 1410–1429.CrossRefGoogle Scholar
Robbins, H. and Siegmund, D. (1973) Statistical tests of power one and the integral representation of solutions of certain partial differential equations. Bull. Inst. Math. Acad. Sinica
1, 93–120.Google Scholar

