Article contents
Functional normalizations for the branching process with infinite mean
Published online by Cambridge University Press: 14 July 2016
Abstract
It is well known that, in a Bienaymé-Galton–Watson process (Zn) with 1 < m = EZ1 < ∞ and EZ1 log Z1 <∞, the sequence of random variables Znm –n converges a.s. to a non–degenerate limit. When m =∞, an analogous result holds: for any 0< α < 1, it is possible to find functions U such that α n U (Zn) converges a.s. to a non-degenerate limit. In this paper, some sufficient conditions, expressed in terms of the probability generating function of Z1 and of its distribution function, are given under which a particular pair (α, U) is appropriate for (Zn). The most stringent set of conditions reduces, when U (x) 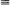 x, to the requirements EZ1 = 1/α, EZ1 log Z1 <∞.
x, to the requirements EZ1 = 1/α, EZ1 log Z1 <∞.
Information
- Type
- Research Papers
- Information
- Copyright
- Copyright © Applied Probability Trust 1979
Footnotes
Present address: Department of Statistics, Richard Berry Building, University of Melbourne Parkville, Victoria 3052, Australia.
References
- 3
- Cited by

