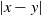Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Gracar, Peter
Grauer, Arne
and
Mörters, Peter
2022.
Chemical Distance in Geometric Random Graphs with Long Edges and Scale-Free Degree Distribution.
Communications in Mathematical Physics,
Vol. 395,
Issue. 2,
p.
859.
Bäumler, Johannes
2023.
Distances in $$\frac{1}{\Vert x-y\Vert ^{2d}}$$ Percolation Models for all Dimensions.
Communications in Mathematical Physics,
Vol. 404,
Issue. 3,
p.
1495.
Komjáthy, Júlia
Lapinskas, John
Lengler, Johannes
and
Schaller, Ulysse
2024.
Polynomial growth in degree-dependent first passage percolation on spatial random graphs.
Electronic Journal of Probability,
Vol. 29,
Issue. none,
Cipriani, Alessandra
and
Salvi, Michele
2024.
Scale-free percolation mixing time.
Stochastic Processes and their Applications,
Vol. 167,
Issue. ,
p.
104236.
Biskup, Marek
and
Krieger, Andrew
2024.
Arithmetic oscillations of the chemical distance in long-range percolation on Zd.
The Annals of Applied Probability,
Vol. 34,
Issue. 3,
Bäumler, Johannes
2025.
Behavior of the distance exponent for 1 |x−y|2d long-range percolation.
Electronic Journal of Probability,
Vol. 30,
Issue. none,