Article contents
Improvements on the distribution of maximal segmental scores in a Markovian sequence
Published online by Cambridge University Press: 04 May 2020
Abstract
Let 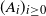 $(A_i)_{i \geq 0}$ be a finite-state irreducible aperiodic Markov chain and f a lattice score function such that the average score is negative and positive scores are possible. Define
$(A_i)_{i \geq 0}$ be a finite-state irreducible aperiodic Markov chain and f a lattice score function such that the average score is negative and positive scores are possible. Define 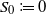 $S_0\coloneqq 0$ and
$S_0\coloneqq 0$ and 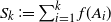 $S_k\coloneqq \sum_{i=1}^k f(A_i)$ the successive partial sums,
$S_k\coloneqq \sum_{i=1}^k f(A_i)$ the successive partial sums, 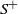 $S^+$ the maximal non-negative partial sum,
$S^+$ the maximal non-negative partial sum, 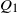 $Q_1$ the maximal segmental score of the first excursion above 0, and
$Q_1$ the maximal segmental score of the first excursion above 0, and 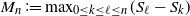 $M_n\coloneqq \max_{0\leq k\leq\ell\leq n} (S_{\ell}-S_k)$ the local score, first defined by Karlin and Altschul (1990). We establish recursive formulae for the exact distribution of
$M_n\coloneqq \max_{0\leq k\leq\ell\leq n} (S_{\ell}-S_k)$ the local score, first defined by Karlin and Altschul (1990). We establish recursive formulae for the exact distribution of 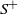 $S^+$ and derive a new approximation for the tail behaviour of
$S^+$ and derive a new approximation for the tail behaviour of 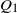 $Q_1$ , together with an asymptotic equivalence for the distribution of
$Q_1$ , together with an asymptotic equivalence for the distribution of 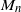 $M_n$ . Computational methods are explicitly presented in a simple application case. The new approximations are compared with those proposed by Karlin and Dembo (1992) in order to evaluate improvements, both in the simple application case and on the real data examples considered by Karlin and Altschul (1990).
$M_n$ . Computational methods are explicitly presented in a simple application case. The new approximations are compared with those proposed by Karlin and Dembo (1992) in order to evaluate improvements, both in the simple application case and on the real data examples considered by Karlin and Altschul (1990).
Information
- Type
- Research Papers
- Information
- Copyright
- © Applied Probability Trust 2020
References
- 2
- Cited by

