Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Deheuvels, Paul
Haeusler, Erich
and
Mason, David M.
1988.
Almost sure convergence of the Hill estimator.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 104,
Issue. 2,
p.
371.
Dargahi-Noubary, G.R.
1988.
Some newly developed statistical procedures for extreme events.
Physics of the Earth and Planetary Interiors,
Vol. 52,
Issue. 1-2,
p.
102.
Dargahi-Noubary, G.R.
1989.
A parametric model for prediction of low toughness values in materials.
Mathematical and Computer Modelling,
Vol. 12,
Issue. 7,
p.
845.
Einmahl, J.H.J.
1990.
The empirical distribution function as a tail estimator.
Statistica Neerlandica,
Vol. 44,
Issue. 2,
p.
79.
Dargahi‐Noubary, G. R.
1992.
Estimation of stress‐strength reliability based on tail‐modelling.
Applied Stochastic Models and Data Analysis,
Vol. 8,
Issue. 1,
p.
17.
Dargahi-Noubary, G. R.
and
Smith, Wm. Steven
2001.
Measuring Investment Risk Based on Tail Thickness.
Review of Quantitative Finance and Accounting,
Vol. 16,
Issue. 1,
p.
81.
El-Aroui, Mhamed-Ali
and
Diebolt, Jean
2002.
On the use of the peaks over thresholds method for estimating out-of-sample quantiles.
Computational Statistics & Data Analysis,
Vol. 39,
Issue. 4,
p.
453.
Dargahi-Noubary, G.R.
2002.
The use of modern statistical theories in the assessment of earthquake hazard, with application to quiet regions of eastern North America.
Soil Dynamics and Earthquake Engineering,
Vol. 22,
Issue. 5,
p.
361.
Biroli, Marco
Larralde, Hernán
Majumdar, Satya N.
and
Schehr, Grégory
2024.
Exact extreme, order, and sum statistics in a class of strongly correlated systems.
Physical Review E,
Vol. 109,
Issue. 1,

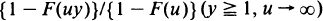 when this is approximated by
when this is approximated by 