Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-10T20:49:34.294Z Has data issue: false hasContentIssue false
  • English
  • Français

Limit motion of an Ornstein–Uhlenbeck particle on the equilibrium manifold of a force field

Part of: Stochastic analysis Markov processes

Published online by Cambridge University Press:  14 July 2016

Antonella Calzolari  and
Federico Marchetti
Antonella Calzolari*
Affiliation:
Università di Roma ‘Tor Vergata'
Federico Marchetti*
Affiliation:
Politecnico di Milano
*
∗Postal address: Dipartimento di Matematica, Università di Roma ‘Tor Vergata', via d. Ricerca Scientifica, 00133 Roma, Italy.
∗Postal address: Dipartimento di Matematica, Università di Roma ‘Tor Vergata', via d. Ricerca Scientifica, 00133 Roma, Italy.
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we consider a position–velocity Ornstein-Uhlenbeck process in an external gradient force field pushing it toward a smoothly imbedded submanifold of 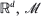. The force is chosen so that 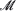is asymptotically stable for the associated deterministic flow. We examine the asymptotic behavior of the system when the force intensity diverges together with the diffusion and the damping coefficients, with appropriate speed. We prove that, under some natural conditions on the initial data, the sequence of position processes is relatively compact, any limit process is constrained on 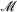, and satisfies an explicit stochastic differential equation which, for compact 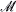, has a unique solution.

Keywords

DIFFUSIONS ON MANIFOLDSORNSTEIN–UHLENBECK PARTICLECONSTRAINTSWEAK CONVERGENCECONVERGENCE OF STOCHASTIC INTEGRALS

MSC classification

Primary: 60H10: Stochastic ordinary differential equations
Secondary: 60J65: Brownian motion
Type
Research Papers
Information
Journal of Applied Probability , Volume 34 , Issue 4 , December 1997 , pp. 924 - 938
Copyright
Copyright © Applied Probability Trust 1997 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ethier, S. N. and Kurtz, T. G. (1986) Markov Processes, Characterization and Convergence. Wiley, New York.Google Scholar
Falconer, K. J. (1983) Differentiation of the limit mapping in a dynamical system. J. London Math. Soc. 27, 356–372.Google Scholar
Funaki, T. and Nagai, H. (1993) Degenerative convergence of diffusion processes toward a submanifold by strong drift. Stoch. Stoch. Rep. 44, 1–25.Google Scholar
Katzenberger, G. S. (1991) Solution of a stochastic differential equation forced onto a manifold by a large drift. Ann. Prob. 19, 1587–1628.Google Scholar
Kurtz, T. G. and Marchetti, F. (1995) Averaging stochastically perturbed Hamiltonian systems. In Proc. Symp. Pure Math. ed. Cranston, M. and Pinsky, M. A. pp. 93–104.Google Scholar
Kurtz, T. G. and Protter, P. (1991) Weak limit theorems for stochastic integrals and stochastic differential equations. Ann. Prob. 19, 1035–1070.Google Scholar
Nash, J. (1954) C1-isometric imbeddings. Ann. Math. 60, 383–396.Google Scholar
Roger, L. C. G. and Williams, D. (1987) Diffusions, Markov Processes, and Martingales. Vol. 2. Wiley, New York.Google Scholar